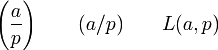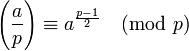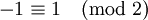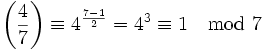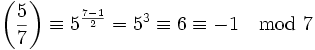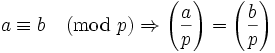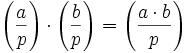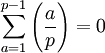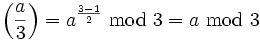Eulersches Kriterium

Das Legendre-Symbol ist eine Kurzschreibweise, die in der Zahlentheorie, einem Teilgebiet der Mathematik, verwendet wird. Es ist nach dem französischen Mathematiker Adrien-Marie Legendre benannt und wird wie folgt notiert:

$\left(\frac{a}{p}\right) \qquad (a/p) \qquad L(a,p)$

Diese drei Notationen geben jeweils an, ob die Zahl a ein Quadratischer Rest modulo p oder Quadratischer Nichtrest modulo p ist. Dabei muss p eine Primzahl sein. Es gilt

$\left(\frac{a}{p}\right) = \begin{cases} 1 & \mbox{wenn } a \mbox{ Quadratischer Rest modulo } p \mbox{ ist} \\ -1 & \mbox{wenn } a \mbox{ Quadratischer Nichtrest modulo } p \mbox{ ist} \\ 0 & \mbox{wenn } a \mbox{ ein Vielfaches von } p \mbox{ ist} \end{cases}$

Das Legendre-Symbol ist ein Spezialfall des Jacobi-Symbols, das die gleiche Schreibweise hat.

Das Eulersche Kriterium gibt an, wie sich das Legendre-Symbol für alle Primzahlen p außer der 2 berechnen lässt:

$\left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}} \pmod p$

Die Zahl 2 wird durch die Formel nicht berücksichtigt, da gilt

$-1 \equiv 1 \pmod 2$

Beispiele

4 ist ein quadratischer Rest zu modulo 7:

$\left(\frac{4}{7}\right) \equiv 4^{\frac{7-1}{2}}= 4^3 \equiv 1\mod7$

5 ist kein quadratischer Rest zu modulo 7:

$\left(\frac{5}{7}\right) \equiv 5^{\frac{7-1}{2}} = 5^3 \equiv 6 \equiv -1 \mod 7$

14 ist durch 7 teilbar:

$\left(\frac{14}{7}\right) \equiv 14^{\frac{7-1}{2}} = 14^3 \equiv 0 \mod7$

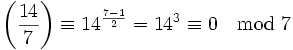
Rechenregeln

Das Quadratische Reziprozitätsgesetz macht wichtige Aussagen über das Rechnen mit dem Legendre-Symbol.

Es seien nun 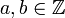$a, b \in \Z$ und p eine Primzahl mit 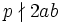$p \nmid 2ab$. Dann gelten folgende Rechenregeln:

• $a \equiv b \pmod p \Rightarrow \left(\frac{a}{p}\right) = \left(\frac{b}{p}\right)$
• $\left(\frac{a}{p}\right) \cdot \left(\frac{b}{p}\right) = \left(\frac{a\cdot b}{p}\right)$
• $\sum_{a=1}^{p-1} \left(\frac{a}{p}\right) = 0$

Die besondere Stellung der Zahl 3

Die Zahl 3 liefert bei der Ganzzahldivision als Modulo die Werte 0, 1 und -1 zurück. Dies entspricht genau den Werten des Legendre-Symbols. Es gilt also:

$\left(\frac{a}{3}\right) = a^{\frac{3-1}{2}}\ \operatorname{mod}\ 3 = a \ \operatorname{mod}\ 3$

Wenn man also ein Legendre-Symbol in Legendre-Symbole der Form 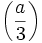$\left(\frac{a}{3}\right)$ zerlegen kann, so lässt sich der Wert, den das Legendre-Symbol zurückliefert, leicht berechnen.