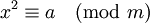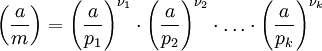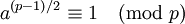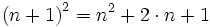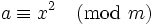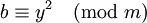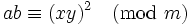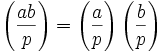Quadratische-Reste-Problem

Der quadratische Rest ist ein Begriff aus dem mathematischen Teilgebiet Zahlentheorie. Eine Zahl a ist ein quadratischer Rest bezüglich eines Moduls m, wenn sie zu m teilerfremd ist und es eine Zahl x gibt, für die die Kongruenz

$x^2 \equiv a \pmod m$

gilt. Für den Spezialfall a < m ist das gleichbedeutend damit, dass a der Rest bei der Division einer Quadratzahl durch m ist:

x²:m = ? Rest a

Existiert für eine zu m teilerfremde Zahl a keine Lösung x der obigen Kongruenz, dann nennt man a quadratischen Nichtrest modulo m. Zu m nicht teilerfremde Zahlen werden nicht klassifiziert.

Betrachtet man beispielsweise den Modul 6, so ist 1 quadratischer Rest und 5 quadratischer Nichtrest. Dies ist sofort ersichtlich, wenn man x²mod 6 für die Zahlen von 0 bis 5 ausrechnet:

x	x2	x2mod 6
0	0	0
1	1	1
2	4	4
3	9	3
4	16	4
5	25	1

Die Zahlen 0, 2, 3 und 4 sind nicht teilerfremd zu 6 und werden deshalb nicht klassifiziert.

Vor allem in der Kryptologie stellt sich vielfach die Aufgabe für eine vorgegebene Zahl und einen bekannten Modul zu entscheiden, ob diese Zahl ein Quadratischer Rest ist. Diese Fragestellung wird als Quadratische-Reste-Problem bezeichnet. Ist der Modul eine Primzahl, so kann dies recht einfach entschieden werden. Andernfalls stellt es sich teilweise recht schwierig dar. Insbesondere besagt die Quadratische-Reste-Annahme, dass es für bestimmte Moduln praktisch nicht möglich ist, diese Frage zu entscheiden.

Für Rechnungen, bei denen man nachweisen will, ob eine Zahl quadratischer Rest ist, stehen zwei Kurzschreibweisen zur Verfügung. Das Legendre-Symbol gibt an, ob eine Zahl quadratischer Rest für einen Primzahlmodul ist:

$\left(\frac{a}{p}\right) = \begin{cases} 1 &amp;amp; \mbox{wenn } a \mbox{ Quadratischer Rest modulo } p \mbox{ ist} \\ -1 &amp;amp; \mbox{wenn } a \mbox{ Quadratischer Nichtrest modulo } p \mbox{ ist} \\ 0 &amp;amp; \mbox{wenn } a \mbox{ ein Vielfaches von } p \mbox{ ist} \end{cases}$

Dieses wird zum Jacobi-Symbol verallgemeinert, das die Berechnung für beliebige Moduln auf deren Primfaktorzerlegung 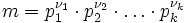$m=p_1^{\nu_1} \cdot p_2^{\nu_2} \cdot \ldots \cdot p_k^{\nu_k}$ zurückführt:

$\left(\frac{a}{m}\right) = \left(\frac{a}{p_1}\right)^{\nu_1} \cdot \left(\frac{a}{p_2}\right)^{\nu_2} \cdot \ldots \cdot \left(\frac{a}{p_k}\right)^{\nu_k}$

Da das Legendre-Symbol für Primzahlmoduln mit dem Jacobi-Symbol identisch ist, ist die Verwendung der gleichen Kurzschreibweise nicht von Nachteil. Als wichtiges Hilfsmittel zur Berechnung des Legendre-Symbols steht das Quadratische Reziprozitätsgesetz mit dem ersten und zweiten Ergänzungssatz zur Verfügung.

Quadratische Reste bei Primzahlmoduln

Ist der Modul eine Primzahl p, so liefert das Eulersche Kriterium ein wichtige Aussage über quadratische Reste. Ein zu p teilerfremdes a ist demnach genau dann ein quadratischer Rest, wenn die folgende Kongruenz gilt:

$a^{(p-1)/2} \equiv 1 \pmod p$

Daraus lässt sich herleiten, dass es bei einem Primzahlmodul genau 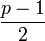$\frac{p-1}{2}$ quadratische Reste und ebensoviele quadratische Nichtreste gibt.

Vereinfachte Berechnung der Quadratzahlen

Für kleinere Zahlen m können die quadratischen Reste relativ rasch berechnet werden: Es genügt, die Zahlen 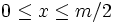$0\leq x\leq m/2$ zu betrachten, denn x² und 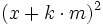$(x+k\cdot m)^2$ haben denselben Rest, ebenso x² und ( − x)², also auch x² und (m − x)².

Die Berechnung wird hier am Beispiel der Zahl 11 demonstriert.

 0 Mod 11 = 0 ;  1 Mod 11 = 1 ;   4 Mod 11 = 4 ;     9 Mod 11 = 9 
16 Mod 11 = 5 ; 25 Mod 11 = 3 ;  36 Mod 11 = 3 ;    49 Mod 11 = 5 
64 Mod 11 = 9 ; 81 Mod 11 = 4 ; 100 Mod 11 = 1 und 121 Mod 11 = 0.

Man könnte jetzt weitermachen, aber der 0,1,4,9,5,3,3,5,9,4,1-Zyklus wiederholt sich immer wieder. Wegen der Symmetriebeziehung ist nur die Berechnung der Quadratzahlen kleiner 36 erforderlich.

Zur Berechnung der Quadratzahlen kann die Beziehung

$\left({n+1}\right)^2 = n^2 + 2 \cdot n +1$

verwendet werden. Die nächste Quadratzahl kann also durch Addition von 2n + 1 ganz ohne Multiplikation berechnet werden. Damit sind die quadratischen Reste für 11 ganz rasch auch im Kopf zu berechnen.

Multiplikative Eigenschaften

Sind a und b quadratische Reste modulo m, dann ist auch ab ein quadratischer Rest. Dies lässt sich einfach zeigen , indem man beide Zahlen multipliziert:

$a \equiv x^2 \pmod m$

$b\equiv y^2 \pmod m$

$ab \equiv (xy)^2 \pmod m$

Der Fall von Primzahlen und das Legendre-Symbol

Im folgenden sei m = p eine Primzahl. Sind a und b nicht durch p teilbar, so gibt die folgende Tabelle in Abhängigkeit von a und b an, ob das Produkt ab quadratischer Rest (R) oder Nichtrest (NR) ist:

	a R	a NR
b R	ab R	ab NR
b NR	ab NR	ab R

Eine andere Formulierung dieser Aussage ist die folgende: Das Legendre-Symbol erfüllt die Beziehung

$\left(\frac{ab}p\right)=\left(\frac ap\right)\left(\frac bp\right)$

Für Primzahlen p > 2 gilt

$\left(\frac ap\right)\equiv a^{(p-1)/2}\mod p.$

Aus dieser Beziehung lässt sich auch unmittelbar die folgende Aussage ablesen: − 1 ist quadratischer Rest modulo Primzahlen der Form 4k + 1 und Nichtrest modulo Primzahlen der Form 4k + 3.

Die Besonderheit der 4

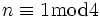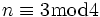Zur Basis der 4 gibt es für die ungeraden Quadratzahlen nur einen quadratischen Rest, nämlich die 1 (für $n \equiv 1 \bmod 4$ oder $n \equiv 3 \bmod 4$ ergibt sich in beiden Fällen 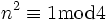$n^2 \equiv 1 \bmod 4$; gerade Zahlen ergeben 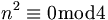$n^2 \equiv 0 \bmod 4$). Die andere ungerade Zahl, die 3, ist demzufolge der quadratische Nichtrest, was bedeutet, dass keine Zahl, nachdem sie quadriert wurde, modulo 4 den Rest 3 lässt. Insbesondere die ungeraden Primzahlen (also p>2) lassen sich nun in zwei Gruppen einteilen:

• In solche Primzahlen p, für die gilt 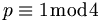$p \equiv 1 \bmod 4$, woraus folgt, dass Quadratzahlen n² existieren, für die gilt: 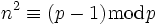$n^2 \equiv (p-1) \bmod p$. Für die Primzahlen dieser Gruppe gilt:

$(p-1)^{\frac{p-1}{2}} \equiv 1 \bmod p$

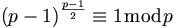
welches der Schreibweise mit dem Legendre-Symbol

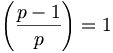$\left(\frac{p-1}{p}\right) = 1$ oder kürzer: 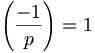$\left(\frac{-1}{p}\right) = 1$ entspricht (nicht mit einem Bruch zu verwechseln!).

• In solche Primzahlen p, für die gilt 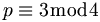$p \equiv 3 \bmod 4$, woraus folgt, dass keine Quadratzahlen n² existieren, für die gilt: 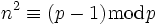$n^2 \equiv (p-1) \bmod p$. Für die Primzahlen dieser Gruppe gilt:

$(p-1)^{\frac{p-1}{2}} \equiv (p-1) \bmod p$.

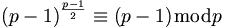Mit dem Legendre-Symbol ausgedrückt:

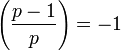$\left(\frac{p-1}{p}\right) = -1$ oder kürzer: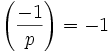 $\left(\frac{-1}{p}\right) = -1$

Alle geraden Quadrat-Zahlen besitzen die 4 als Faktor, was sich einfach zeigen lässt: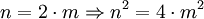 $n = 2 \cdot m \Rightarrow n^2 = 4\cdot m^2$. Daraus folgt, dass für jede gerade Quadratzahl n² gilt: $n^2 \equiv 0 \bmod 4$.

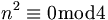Quellen

• Peter Bundschuh: Einführung in die Zahlentheorie. 5. Auflage. Springer, 2002, ISBN 3-540-43579-4, S. 124 und 127–147