Falk-schema

Das falksche Schema (benannt nach Sigurd Falk) ist eine Tabelle, die eine optische Hilfe bei der Matrizenmultiplikation von Hand bietet. Der linke Faktor, die (m × r)-Matrix, wird links von der (m × n)-Ergebnismatrix und der rechte Faktor, die (r × n)-Matrix, wird oberhalb der Ergebnismatrix platziert. Wo sich die i-te Zeile des linken Multiplikanden und die j-te Spalte des rechten Multiplikanden kreuzen, wird das entsprechende Skalarprodukt eingetragen.

Beispiel

Gegeben sind die Matrizen

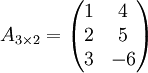$A_{3 \times 2 } = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & -6 \end{pmatrix}$ und $B_{2 \times 2 }= \begin{pmatrix} -1 & 1 \\ 1 & -2 \\ \end{pmatrix}$ .

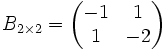Es soll das Produkt C = A · B ermittelt werden. C ist eine 3 × 2-Matrix.

Spalte k  1  2  -1  1   Zeile i                1  -2  1  1  4  2  2  5  3  3  -6

Es wird das falksche Schema aufgestellt, indem die Matrizen höhenversetzt nebeneinander geschrieben werden (in der ursprünglichen Ausrichtung, also ohne Kippen oder Drehen).

Spalte k  1  2  -1  1   Zeile i                1  -2  1  1  4  3  2  2  5  3  3  -6

Die erste Zeile von A wird elementweise mit der ersten Spalte von B multipliziert: 1 · (-1) + 4 · 1 = 3 und ergibt das Element c11 = 3.

Spalte k  1  2  -1  1   Zeile i                1  -2  1  1  4  3  -7  2  2  5  3  3  -6

Die erste Zeile von A wird elementweise mit der zweiten Spalte von B multipliziert: 1 · 1 + 4 · (-2) = -7 und ergibt das Element c12 = -7.

...

Spalte k  1  2  -1  1   Zeile i                1  -2  1  1  4  3  -7  2  2  5  3  -8  3  3  -6  -9  15

Die dritte Zeile von A wird elementweise mit der zweiten Spalte von B multipliziert: 3 · 1 + (-6) · (-2) = 15 und ergibt das Element c32 = 15.