Fiat-Shamir-Protokoll

Das Fiat-Shamir-Protokoll ist ein Protokoll aus dem Gebiet der Kryptografie, mit dem man sich jemandem gegenüber authentisieren kann. Dazu zeigt man, dass man eine Quadratwurzel (privater Schlüssel) einer vorher veröffentlichten Quadratzahl (öffentlicher Schlüssel) kennt. Bei dem Verfahren wird nur ein einziges Bit des privaten Schlüssels preisgegeben, nämlich das Vorzeichen. Eine Variante ist das Feige-Fiat-Shamir-Protokoll, bei dem keine Information über den privaten Schlüssel preisgegeben wird. Man spricht deswegen von einem Zero-Knowledge-Protokoll. Insbesondere ist das Protokoll perfekt zero-knowledge. Das heißt, es gibt einen Simulations-Algorithmus, der in polynomieller Zeit eine Mitschrift erzeugt, die von einer echten Interaktion nicht zu unterscheiden ist.

Das Fiat-Shamir-Protokoll wurde im Jahr 1986 von Amos Fiat und Adi Shamir vorgestellt. An der Entwicklung des Feige-Fiat-Shamir-Protokolls war auch Uriel Feige beteiligt.

Das Verfahren arbeitet interaktiv, das heißt, es finden mehrere Runden zwischen Geheimnisträger und dem Prüfer statt. In jeder Runde kann die Kenntnis der Zahl zu 50 % bewiesen werden. Nach zwei Runden bleibt eine Unsicherheit von 25 %, nach der dritten Runde nur noch 12,5 % usw. Nach n Runden beträgt die Unsicherheit 2 ^{− n}.

Die Sicherheit des Fiat-Shamir-Protokolls beruht auf der Schwierigkeit, Quadratwurzeln im Restklassenring $\Z_n$ zu berechnen. Diese Berechnung ist genauso schwierig, wie die Zahl $n=p\cdot q$ (p und q sind Primzahlen) zu faktorisieren und damit praktisch nicht durchführbar, wenn die Zahlen hinreichend groß sind.

Protokoll

Beim Fiat-Shamir-Protokoll wird eine vertrauenswürdige dritte Partei benötigt. Diese veröffentlicht einen RSA-Modul $n = p \cdot q$, dessen Primfaktoren p und q sie geheimhält. Die Beweiserin (Geheimnisträgerin) Peggy wählt eine zu n teilerfremde Zahl s als persönliches Geheimnis, mit dem sie sich Victor (V wie Verifizierer) gegenüber authentisieren will. Diese darf sie niemandem weitergeben. 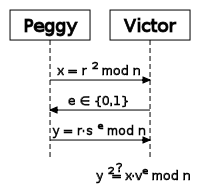Sie berechnet $v \equiv s^2 \bmod n$ und registriert v als öffentlichen Schlüssel bei der dritten Partei.

Eine einzelne Runde im Fiat-Shamir-Protokoll besteht aus den folgenden Aktionen:

1. Peggy wählt eine Zufallszahl r, berechnet $x \equiv r^2 \bmod n$ und sendet x an Victor.
2. Victor wählt zufällig ein $e \in \{0,1\}$ und sendet dies an Peggy.
3. Peggy berechnet $y = r \cdot s^e \bmod n$ und sendet y an Victor.
4. Victor überprüft, ob $y^2 \equiv x \cdot v^e \pmod n$ gilt.

Dieses Protokoll ist noch nicht Zero-Knowledge, da es ein Bit Information über $r \, \bmod n$ preisgibt: Würde Viktor auf irgendeine Weise erfahren, dass $r \equiv \pm \, c \, \bmod n$ für eine Zahl c gilt, könnte er nach Ausführung des Protokolls sicher entscheiden, ob $r \equiv c \, \bmod n$ oder $r \equiv -c \, \bmod n$ gilt; er hätte das fehlende Bit Information (das Vorzeichen von c bzw. r) also aus den Daten des Protokolls gewonnen.

Im Feige-Fiat-Shamir-Protokoll sendet Peggy im ersten Schritt entweder x oder $-x \, \bmod n$ an Victor. Die Wahl, welchen Wert sie sendet, trifft sie zufällig. Viktor prüft dann im letzten Schritt, dass entweder $y^2 \equiv x \cdot v^e \bmod n$ oder $y^2 \equiv -x \cdot v^e \bmod n$ gilt. Dadurch wird auch das Vorzeichen von c nicht preisgegeben und das Protokoll ist Zero-Knowledge.

Schwächen

Für die Sicherheit des Protokolls ist die Wahl der Zufallszahl r von großer Bedeutung.
Wird dasselbe r zweimal verwendet und ist e dabei einmal 0 und einmal 1, lässt sich der private Schlüssel berechnen.

Beispiel

In beiden Fällen hat $x \equiv r^2 \bmod n$ den selben Wert.

1. Runde
   • e₁ = 0
   • Peggy überträgt: $y_1 \equiv r \, \bmod n$
2. Runde
   • e₂ = 1
   • Peggy überträgt: $y_2 \equiv r \cdot s \bmod n$

Ein Angreifer kann nun einfach s berechnen. Damit ist s kein Geheimnis mehr, das nur Peggy kennt.
$s \equiv y_2 \cdot r^{-1} \equiv y_2 \cdot y_1^{-1} \bmod n$

Quellen

• Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Moderne Verfahren der Kryptographie. Vieweg+Teubner, Braunschweig/Wiesbaden 2010, 7. Auflage, ISBN 978-3-8348-1228-5, S. 49–50
• Amos Fiat, Adi Shamir: How to Prove Yourself: Practical Solutions to Identification and Signature Problems. In: Proceedings on Advances in Cryptology - CRYPTO '86. Springer-Verlag, 1987, ISBN 0-387-18047-8, S. 186–194