Finale Topologie

Als Finaltopologie bezüglich einer Abbildungsfamilie bezeichnet man in der Topologie die feinste Topologie auf einer Menge X, die diese Familie von Abbildungen aus anderen topologischen Räumen nach X stetig macht. Die Finaltopologie entsteht also durch „Vorwärtsübertragung“ der auf den Urbildräumen vorhandenen topologischen Strukturen auf die Menge X. Dies ist die Anwendung eines allgemeineren Konzepts aus der Kategorientheorie auf topologische Räume, mit der wichtige „natürliche Räume“ wie Quotienten- und Summentopologie in einen gemeinsamen Rahmen gestellt werden können.

Definition

Gegeben ist eine Menge X, eine Familie von topologischen Räumen (Y_i,T_i) und eine Familie von Abbildungen f_i :Y_i → X . Eine Topologie S auf X heißt Finaltopologie bezüglich der Familie (Y_i,T_i,f_i) wenn sie eine der folgenden gleichwertigen Eigenschaften hat:

1. S ist die feinste Topologie auf X, bezüglich der alle Abbildungen f_i stetig sind.
2. Eine Teilmenge O von X ist offen (also in S) genau dann, wenn alle ihre Urbilder 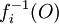$f_i^{-1}(O)$ in den jeweiligen Urbildräumen offen sind.
3. Eine Funktion g von X in einen topologischen Raum Z ist genau dann stetig, wenn 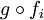$g \circ f_i$ stetig ist für jedes f_i der Familie.

Bemerkungen

Die drei Formulierungen der Definition beleuchten unterschiedliche Aspekte der Finaltopologie:

1. Hier wird sie als Infimum gewisser Topologien im Verband aller Topologien auf X angesehen: Durch jede einzelne Abbildung f_i wird aus dem Urbildraum Y_i eine topologische Struktur S_i auf X übertragen und die Finaltopologie S ist in all diesen Strukturen enthalten. Mit dieser Definition lässt sich die Existenz der Finaltopologie beweisen.
2. Diese Definition ist konstruktiv. Mit ihr kann man für beliebige Teilmengen von X entscheiden, ob sie in der Finaltopologie offen sind. Hieraus ergibt sich leicht die Eindeutigkeit dieser Topologie.
3. Die abstrakte Charakterisierung durch eine universelle Eigenschaft rechtfertigt die Bezeichnung „Final“-Topologie und gestattet es, diese Strukturen im allgemeineren Rahmen der Kategorientheorie zu betrachten. Die Initialtopologie kann durch die hierzu duale Eigenschaft charakterisiert werden.

Beispiele

• Die Quotiententopologie ist die Finaltopologie bezüglich der kanonischen Projektion auf den Quotientenraum.
• Der Topologische Summenraum einer Familie X_i von Topologischen Räumen ist die Finaltopologie auf der disjunkten Vereinigungsmenge der Familie bezüglich der kanonischen Inklusionsabbildungen.
• Die Kombination der Summen- und Quotientenraumbildung, d. i. das „Verkleben“ mehrerer Topologischer Räume, kann mit der Finaltopologie in einem Schritt vorgenommen werden.

Literatur

• Boto von Querenburg: Mengentheoretische Topologie. 2. Auflage. Springer-Verlag, 1979, ISBN 3-540-09799-6