Verband (Mathematik)

In der Mathematik ist ein Verband eine bestimmte algebraische Struktur mit zwei Verknüpfungen bzw. eine halbgeordnete Menge mit bestimmten Eigenschaften.

Definition

Ein Verband (V, $\cup$, $\cap$) ist eine nichtleere Menge V mit zwei inneren binären Verknüpfungen $\cup$ (Vereinigung, engl. join), und $\cap$ (Durchschnitt, engl. meet), die folgenden Bedingungen für alle u, v, w aus V genügen:

Assoziativität:

• u $\cup$ ( v $\cup$ w ) = ( u $\cup$ v ) $\cup$ w, und
• u $\cap$ ( v $\cap$ w ) = ( u $\cap$ v ) $\cap$ w;

Kommutativität:

• u $\cup$ v = v $\cup$ u, und
• u $\cap$ v = v $\cap$ u;

Absorptionsgesetze:

• u $\cup$ ( u $\cap$ v ) = u, und
• u $\cap$ ( u $\cup$ v ) = u.

Aus diesen Bedingungen folgt die Idempotenz beider Verknüpfungen:

• u $\cup$ u = u, und
• u $\cap$ u = u.

V ist also bezüglich jeder einzelnen Verknüpfung ein Halbverband, d. h. eine kommutative Halbgruppe, in der jedes Element idempotent ist. Die Verknüpfungen treten bei den Absorptionsgesetzen in Wechselwirkung.

Vertauscht man die beiden Verknüpfungen, erhält man den zu V dualen Verband.

Verbandsordnung

Man kann nach einer Idee von Leibniz auf V eine Halbordnung definieren durch:

• $v\leq w \quad\iff\quad v\cap w = v.$

Mit dem Absorptionsgesetz erkennt man die Gültigkeit der Äquivalenzen

• $v\leq w \quad\iff\quad v\cap w=v\quad\iff\quad v\cup w=w.$

Bezüglich dieser Halbordnung hat jede zweielementige Teilmenge {v, w} ein Supremum (obere Grenze) $s = v \cup w$ und ein Infimum (untere Grenze) $i = v \cap w$. Dabei ist ein Element s ein Supremum von {v, w}, wenn gilt

• $v \leq s$ und $w \leq s$ (d. h. s ist obere Schranke)
• aus $v \leq t$ und $w \leq t$ folgt $s \leq t$ (d. h. s ist die kleinste obere Schranke).

Analoges gilt für das Infimum i. Man kann per Induktion zeigen, dass jede nichtleere endliche Teilmenge ein Supremum und ein Infimum hat. Man schreibt allgemein das Supremum einer Menge M als $\bigcup M$, und das Infimum von M als $\bigcap M$, falls diese existieren.

Umgekehrt kann man für eine halbgeordnete Menge, bei der jede zweielementige Teilmenge ein Infimum und ein Supremum hat, zwei Verknüpfungen definieren, die die Verbandsaxiome erfüllen.

Die Ordnung des dualen Verbandes ist die umgekehrte Ordnung (aus kleinergleich wird größergleich).

Wenn jede bezüglich der Ordnung totalgeordnete Teilmenge (Kette) endlich ist, nennt man den Verband längenendlich.^[1]

Hasse-Diagramme

Eine endliche halbgeordnete Menge (M, ≤) kann man durch einen gerichteten Graphen darstellen, den man Hasse-Diagramm nennt. Dieser Graph enthält alle Elemente von M als Knoten. Die Kanten werden nach folgender Regel eingefügt:

• Sind a und b Elemente von M, sodass a < b ist und es kein Element zwischen a und b gibt (d. h. kein c mit a < c < b), dann geht von a nach b eine Kante.

Solch ein Graph kann so angeordnet werden, dass alle Kanten „von unten nach oben“ gerichtet sind. Ist also a < b, dann ist a unterhalb von b und durch eine Kante mit b verbunden. Einige solcher Diagramme sind weiter unten angegeben.

Vom Aussehen dieser Diagramme leitet sich der englische Name lattice (Gitter) für Verband ab.

Spezielle Verbände

Im folgenden meinen wir mit dem „Verband V“ stets den Verband (V, $\cup$, $\cap$).

Ein Verband V heißt distributiv, wenn die Verknüpfungen in doppelter Hinsicht distributiv sind:

• $u\cup(v\cap w) = (u\cup v)\cap(u\cup w)$ für alle $u,v,w\in V$ und
• $u\cap(v\cup w) = (u\cap v)\cup(u\cap w)$ für alle $u,v,w\in V$.

Da diese beiden Aussagen zueinander äquivalent sind, genügt es, die Gültigkeit eines dieser beiden Distributivgesetze zu verlangen.

Ein Verband V heißt modular, falls gilt:

• $u\leq w \Longrightarrow u\cup(v\cap w) = (u\cup v)\cap w$ für alle $u,v,w\in V$.

Für einen Verband V sind wiederum jeweils äquivalent:

• V ist modular.
• $u\geq w \Longrightarrow u\cap(v\cup w) = (u\cap v)\cup w$ für alle $u,v,w\in V$.
• $u\cup(v\cap(u\cup w)) = (u\cup v)\cap(u\cup w)$ für alle $u,v,w\in V$.
• $u\cap(v\cup(u\cap w)) = (u\cap v)\cup(u\cap w)$ für alle $u,v,w\in V$.

Jeder distributive Verband ist modular, aber nicht umgekehrt. Ein nicht modularer Verband enthält immer den Verband N₅ als Unterverband.

Falls die Verknüpfung $\cup$ ein neutrales Element 0 hat,

• $a \cup 0 = a,$

dann nennt man es das Nullelement des Verbandes. Es ist eindeutig bestimmt und bzgl. der Ordnung das kleinste Element:

• $a \cap 0 = 0$ und $0 = \bigcap V.$

Man nennt den Verband dann nach unten beschränkt.

Falls die Verknüpfung $\cap$ ein neutrales Element 1 hat,

• $a \cap 1 = a,$

dann nennt man es das Einselement' des Verbandes. Es ist eindeutig bestimmt und bzgl. der Ordnung das größte Element:

• $a \cup 1 = 1$ und $1 = \bigcup V.$

Man nennt den Verband dann nach oben beschränkt.

Das neutrale Element der einen Verknüpfung ist also ein absorbierendes Element der anderen Verknüpfung. Ein Verband heißt beschränkt, wenn er nach oben und nach unten beschränkt ist, also für beide Verknüpfungen ein neutrales Element hat.

Für ein gegebenes Element a eines beschränkten Verbandes nennt man ein Element b mit der Eigenschaft

• $a \cap b = 0$ und $a \cup b = 1$

ein Komplement von a. Ein beschränkter Verband, in dem jedes Element ein Komplement hat, heißt komplementär.

Ein distributiver komplementärer Verband heißt Boolesche Algebra oder Boolescher Verband; wenn statt des Komplements nur ein sog. relatives Pseudokomplement existiert, spricht man von einer Heyting-Algebra.

Ein Verband V heißt vollständig, wenn jede (auch die leere ebenso wie gegebenenfalls unendliche) Teilmenge ein Supremum und ein Infimum hat.

Es genügt, für jede Teilmenge M die Existenz des Supremums zu verlangen, denn es ist

• $\bigcap M = \bigcup \{ x \in V : (\forall\,y\in M: x \le y) \}.$

Man nennt ein Element a eines vollständigen Verbandes V kompakt (nach der verwandten Eigenschaft kompakter Räume in der Topologie), wenn jede Teilmenge M von V mit

• $a\leq\bigcup M$

eine endliche Teilmenge E enthält, für die gilt:

• $a\leq\bigcup E$.

Ein Verband V heißt algebraisch, wenn er vollständig ist und wenn jedes Element von V das Supremum von kompakten Elementen ist.

Eigenschaften

Jeder vollständige Verband V ist beschränkt mit

• $0 = \bigcap V = \bigcup \emptyset$ und $1 = \bigcup V = \bigcap \emptyset.$

Jeder endliche, nichtleere Verband V ist vollständig, also auch beschränkt.

In einem distributiven beschränkten Verband ist das Komplement eines Elements a im Falle seiner Existenz eindeutig bestimmt, man schreibt es oft als a^c (vor allem bei Teilmengenverbänden) oder ¬a (vor allem bei Anwendungen in der Logik).

• Beweis: Seien b und c Komplemente von a, dann wollen wir b = c zeigen. Nun ist b = b $\cap$ 1 = b $\cap$ (a $\cup$c) = (b $\cap$ a ) $\cup$ (b $\cap$ c) = b $\cap$ c. Ähnlich zeigt man c = b $\cap$ c, somit b = c.

Ist der Verband jedoch nicht distributiv, kann es mehrere Komplemente geben, ein Beispiel wird unten gegeben.

In einem distributiven beschränkten Verband gilt

• ¬0 = 1, ¬1 = 0.

Falls a ein Komplement ¬a hat, dann hat auch ¬a ein Komplement, nämlich:

• ¬(¬a) = a.

Für weitere Eigenschaften Boolescher Verbände siehe dort.

Homomorphismen und Unterverbände

Zum Beispiel ist die hier dargestellte monotone Abbildung f zwischen den Verbänden V und W kein Homomorphismus, da f(b $\cup$ c) = n, aber f(b) $\cup$ f(c) = m. Außerdem ist aus demselben Grund das Bild f(V) = {j,k,l,n} zwar ein Verband (mit $k \cup l = n$), aber kein Unterverband von W.

Sind $(V,\sqcup,\sqcap)$ und $(W,\cup,\cap)$ zwei Verbände und $f\colon\, V \to W$ eine Funktion, sodass für alle a, b aus V gilt

• $f(a\sqcup b) = f(a)\cup f(b),$
• $f(a\sqcap b) = f(a)\cap f(b),$

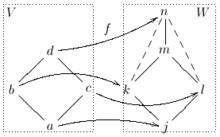
dann heißt f Verbandshomomorphismus. Ist f zusätzlich bijektiv, dann heißt f Isomorphismus und die Verbände V und W sind isomorph.

Falls $(V,\sqcup,\sqcap)$ und $(W,\cup,\cap)$ vollständig sind und $f\colon\, V \to W$ sogar

• $f(\bigsqcup T) = \bigcup \{f(a) \mid a \in T\},$
• $f(\bigl\lceil\!\begin{matrix}-\\\;\end{matrix}\!\bigr\rceil T) = \bigcap \{f(a) \mid a \in T\}$

für alle $T \subseteq V$ erfüllt, nennt man f einen vollständigen Verbandshomomorphismus. Jeder vollständige Verbandshomomorphismus ist offensichtlich auch ein Verbandshomomorphismus.

Die Klasse aller Verbände bildet mit diesen Homomorphismusbegriffen jeweils eine Kategorie.

Ein Verbandshomomorphismus ist gleichzeitig ein Ordnungshomomorphismus, d. h. eine isotone Abbildung:

• aus $a \leq b$ folgt $f(a) \leq f(b).$

Jedoch ist nicht jede isotone Abbildung zwischen Verbänden ein Verbandshomomorphismus.

Ein Unterverband von V ist eine Teilmenge U, die mit den eingeschränkten Verknüpfungen von V ein Verband ist, d. h. es liegen

• $a \cup b$ und $a \cap b$ in U

für alle a,b aus U.

Jeder Unterverband ist wieder eine halbgeordnete Menge mit Supremum und Infimum für endliche Teilmengen, aber nicht jede halbgeordnete Teilmenge mit Supremum und Infimum für endliche Teilmengen ist auch ein Unterverband, das gilt erst, wenn es dieselben Infima und Suprema wie im großen Verband sind.

Beispiele für Verbände

Hier folgen Beispiele für bestimmte Situationen, in denen auf natürliche Weise Verbände auftreten, und weiter unten grafische Darstellungen einzelner Verbände und halbgeordneter Mengen, die keinen Verband darstellen.

Total geordnete Menge

Jede total geordnete Menge M ist ein distributiver Verband mit den Verknüpfungen Maximum und Minimum. Insbesondere gilt für alle a,b,c aus M:

• max(a, min(b, c)) = min(max(a,b), max(a,c)),
• min(a, max(b, c)) = max(min(a,b), min(a,c)).

Nur im Fall einer ein- oder zweielementigen Menge M ist der Verband komplementär.

Beispiele für die übrigen Eigenschaften:

• Das abgeschlossene reelle Intervall [0, 1] und die erweiterte reelle Gerade (R mit ∞ und -∞) sind jeweils vollständige distributive Verbände (und damit beschränkt).
• Das offene reelle Intervall (0, 1), die Mengen R, Q und Z sind jeweils unvollständige unbeschränkte distributive Verbände.
• Das rationale Intervall [0, 1] $\cap$ Q ist ein unvollständiger beschränkter distributiver Verband.
• Die Menge N₀ ist ein unvollständiger distributiver Verband mit Nullelement 0.

Teilerverband

Betrachtet man für eine natürliche Zahl n die Menge T aller Teiler von n, dann ist (T, ggT, kgV) ein vollständiger distributiver Verband mit Einselement n (neutralem Element für ggT) und Nullelement 1 (neutralem Element für kgV). Er heißt Teilerverband von n. Die Absorptionsgesetze und Distributivgesetze für ggT und kgV folgen dabei z. B. mit der Primfaktorzerlegung aus den Eigenschaften von max und min, man kann sie aber auch durch Teilbarkeitsbetrachtungen herleiten. Der Verband ist genau dann komplementär (und damit boolesch), wenn n quadratfrei ist, d. h. wenn n keine Quadratzahl $\ne 1$ als Teiler hat. Die Halbordnung auf T ist die Teiler-Relation:

• a ≤ b genau dann, wenn a|b (genau dann, wenn ggT(a,b) = a).

Teilmengenverband

Für eine Menge M bildet die Potenzmenge $\mathcal P(M)$ mit den Verknüpfungen Vereinigung $\cup$ und Durchschnitt $\cap$ einen algebraischen booleschen Verband mit Nullelement {} (neutrales Element bezüglich $\cup$) und Einselement M (neutrales Element bezüglich $\cap$) sowie Komplement $A^c = M\setminus A$ für alle $A \in \mathcal P(M)$. Er heißt Potenzmengen- oder Teilmengenverband von M. Die Halbordnung auf $(\mathcal P(M),\cup,\cap)$ ist die Mengeninklusion:

• $A \leq B,$ falls $A \subseteq B$ (oder äquivalent dazu $A \cap B = A.$)

(Trägermengen von) Unterverbände(n) von $(\mathcal P(M),\cup,\cap)$ heißen Mengenverbände (zwischen den Verbänden und ihren Trägermengen wird oft nicht unterschieden). Diese Verbände sind immer distributiv, müssen jedoch weder vollständig sein, noch neutrale Elemente oder Komplemente haben. (Ein Beispiel dafür ist der Verband der rechts-unendlichen reellen Intervalle $[a,\infty)$ mit a aus $\R$, der isomorph zum Verband der reellen Zahlen ist.)

Umgekehrt gilt nach dem Darstellungssatz von Priestley:

• Jeder distributive Verband ist isomorph zu(m Verband von) einem Mengenverband.

Unterstrukturenverband einer algebraischen Struktur, Untergruppenverband

Für eine Gruppe (G, *) bildet die Menge A aller Untergruppen von G einen algebraischen (im allgemeinen nicht modularen und damit auch nicht distributiven) Verband mit den Verknüpfungen „Erzeugnis der Vereinigung“ und „Durchschnitt“. Er heißt Untergruppenverband von G.

Beispielsweise hat der Untergruppenverband der kleinschen Vierergruppe {e,a,b,c} (mit neutralem Element e) folgende Struktur:

     {e,a,b,c}
     /   |   \
 {e,a} {e,b} {e,c}
     \   |   /
        {e}

Dieser Verband ist nicht distributiv, denn z. B. hat die Untergruppe {e,a} die zwei Komplemente {e,b} und {e,c}, er ist aber noch modular.

Ebenso bilden

• die normalen Untergruppen einer Gruppe,
• die Untergruppen einer abelschen (= kommutativen) Gruppe,
• die Unterringe eines Ringes,
• die Unterkörper eines Körpers,
• die Untermoduln eines Moduls,
• die Ideale eines Ringes

mit analogen Verknüpfungen einen modularen algebraischen Verband. Die Untergruppen einer beliebigen Gruppe und die Unterverbände eines beliebigen Verbands ergeben zwar immer einen algebraischen Verband, dieser muss aber nicht modular sein.

Ganz allgemein bilden die (algebraischen) Unterstrukturen einer algebraischen Struktur stets einen algebraischen Verband (wobei auch die leere Menge als Unterstruktur betrachtet wird, falls der mengentheoretische Durchschnitt – also das Infimum bezüglich der Mengeninklusion – von der Menge aller Unterstrukturen leer ist).

Insbesondere ist ein Verband genau dann algebraisch, wenn er isomorph ist zum Verband der (algebraischen) Unterstrukturen einer algebraischen Struktur (daher auch der Name „algebraischer Verband“).

Schränkt man die Menge der Untergruppen auf Obergruppen einer festen Untergruppe U ein, so bilden alle diese Zwischengruppen {V : U ≤ V ≤ G} auch einen beschränkten Verband. Analog dazu gibt es Verbände von Zwischenringen, Zwischenkörpern, Zwischenmoduln, Zwischenidealen.

Besonderes Interesse hat man am Untergruppenverband der Galoisgruppe einer galoisschen Körpererweiterung L/K, denn er ist isomorph zum dualen Zwischenkörperverband von L/K.

Diagramme einiger Verbände und Nicht-Verbände

Beispiele für Teilerverbände und dazu isomorphe Mengenverbände

Teilerverband	Graphen
Teilerverband von 3 Teilmengenverband von {1}	3 | 1	{1} | { }
Teilerverband von 6 = 2·3 Teilmengenverband von {1,2}	6 / \ 2 3 \ / 1	{1,2} / \ {1} {2} \ / { }
Teilerverband von 30 = 2·3·5 (Teilmengenverband von {1,2,3})	Teilerverband von 30
Teilerverband von 12 = 22·3 Mengenverband { {}, {1}, {2}, {1,2}, {1,3}, {1,2,3} } distributiv mit neutralen Elementen, nicht komplementär	12 / \ 4 6 | / | 2 3 \ / 1	{1,2,3} / \ {1,3} {1,2} | / | {1} {2} \ / { }

Andere Beispiele für Verbände

Teilerverband	Graph
Verband (N0, min, max): distributiv, Nullelement 0, kein Einselement, Ordnung ist die gewöhnliche Anordnung	: : | 2 | 1 | 0
Der Verband (N0, kgV, ggT): distributiv, Nullelement 1, Einselement 0, nicht komplementär, enthält jeden Teilerverband als Teilverband
Untergruppenverband der Kleinschen Vierergruppe {e,a,b,c}: nicht distributiv, Nullelement {e,a,b,c}, Einselement {e}, nicht komplementär: die Komplemente von {e,a} sind {e,b} und {e,c}.	{e,a,b,c} / | \ {e,a} {e,b} {e,c} \ | / {e}

Weitere Beispiele

	Graph
Kein Verband, da {a, b} keine obere Schranke hat.	a b | \/ | | /\ | c d
Kein Verband, da {c, d} zwar obere Schranken a, b, e hat, aber keine kleinste obere Schranke, weil a und b nicht vergleichbar sind.	e / \ a b | \/ | | /\ | c d \ / f

Literatur

• Garrett Birkhoff: Lattice Theory. 3rd Edition, AMS, Providence, RI 1973, ISBN 0-8218-1025-1.
• Hans Hermes: Einführung in die Verbandstheorie. 2te Auflage, Springer-Verlag, Berlin - Heidelberg 1967.
• Gábor Szász: Einführung in die Verbandstheorie. Akademiai Kiado, Budapest 1962.
• Hilda Draškovičová: Ordered Sets and Lattices. AMS, 1992, ISBN 0821831216.

Weblinks

 Commons: Verband – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ Helmuth Gericke: Theorie der Verbände, Bibliographisches Institut, Mannheim 1963, §6.2