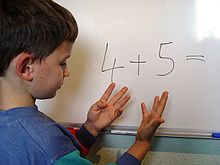Fingerrechnen

Schüler beim Fingerrechnen

Als Fingerrechnen bezeichnet man Methoden, bei denen das Rechnen durch systematischen Einsatz der Finger als Rechenhilfsmittel durchgeführt wird. Es wird vermutet, dass solche Systeme schon im Altertum existierten. Auch der Erfolg des Dezimalsystems geht auf das Fingerrechnen zurück, da der Mensch zehn Finger hat und der Umbruch auf die nächsthöhere Stelle am Ende der Fingerzahl praktisch war (vgl. auch Sexagesimalsystem).

Eine schon sehr alte Form der Rechenhilfe ist der Abakus, der ebenfalls dezimal und mit dem Fingerrechnen leicht kompatibel ist.

Geschichte, Beda Venerabilis, Leonardo Fibonacci

Die erste bekannte Niederschrift stammt von dem englischen Benediktinermönch Beda Venerabilis (um 673-735). In seinem Buch De ratione temporum lieferte er eine vollständige Erklärung der Fingerzählweise und stellte geordnete Regeln für das Rechnen damit auf.

Das Fingerrechnen war bei den Gelehrten, weil das Rechenmittel immer zur Hand war, so populär, dass ein Rechenhandbuch im Mittelalter nur mit einer Beschreibung dieser Methode als vollständig galt. Auch in Fibonaccis berühmtem Rechenbuch Liber abaci, einem enzyklopädischen Rechenbuch, das der westlichen Welt die arithmetischen Rechenmethoden auf der Basis des indisch-arabischen Stellenwertsystems vermittelte, findet sich am Ende des ersten Kapitels ein ausgeklügeltes System von Fingerzahlen und Rechenregeln.

Die Fertigkeiten des Fingerrechnens erhielten sich in verschiedenen Kulturkreisen über einen langen Zeitraum und wurden im mitteleuropäischen Raum erst durch den Sieg des schriftlichen Rechnens mit den indisch-arabischen Ziffern in den Hintergrund gedrängt.

Fingerrechnen nach Anna Schnasing

Eine der überlieferten Formen ist das Fingerrechnen nach Anna Schnasing, eine Methode, mit der die Multiplikation von ganzen Zahlen unter Zuhilfenahme beider Hände so vereinfacht und aufgesplittet wird, dass alle Ergebnisse des kleinen Einmaleins lediglich durch simple Addition ermittelbar werden. Mit Händen und Füßen sind sogar Ergebnisse aus dem großen Einmaleins ermittelbar, die Faktoren dürfen dabei aber nicht größer als 20 sein.

Die Methode funktioniert mit allen Operationen des kleinen Einmaleins bis zur 10 ohne Kenntnisse der auswendig zu lernenden 36 Ergebnisse). Außerdem kann sie durch gedachte Zuhilfenahme der Fußzehen auch auf das große Einmaleins bis zur 20 erweitert werden, was bereits das Erlernen von 400 (20 × 20) Ergebnissen erspart. Die Zehen werden dabei im Schuh leicht bewegt oder bewegt gedacht. (Von Anna vermutlich nicht verwendet.) In jedem Fall muss der Anwender nur addieren können, dann wird er mit etwas Übung viele kassentypische Rechnungen in kurzer Zeit ausführen. Die Methoden von Anna zählen heute zum Fingerrechnen, das mitunter ersatzweise in der Sonderpädagogik eingesetzt wird. Für den Alltag sind sie heute nicht mehr nötig. Sie eignen sich aber für Dyskalkulie und Behinderte sehr gut.

(A) Multiplikation zweier Faktoren bis 5

Diese triviale Fingerrechnung wurde von Anna verwendet.

1. Beide geschlossene Fäuste werden vor den Körper gehalten.
2. Die linke Hand streckt so viele Finger aus, wie die Zahl eines Faktors ist.
3. Die rechte Hand streckt so viele Finger aus, wie die Zahl des zweiten Faktors ist.
4. Nun wird die Zahl der linken Hand so oft mit sich selbst addiert, wie man rechts Finger wieder einknicken kann.

(B) Multiplikation eines Faktors bis 5 mit einem Faktor über 5

1. Beide geschlossene Fäuste werden vor den Körper gehalten.
2. Die linke Hand streckt so viele Finger aus, wie die Zahl des kleineren Faktors ist.
3. Die rechte Hand streckt so viele Finger aus, wie die Zahl des größeren Faktors ist, knickt aber ab 6 die Finger wieder ein. Die 9 hat beispielsweise einen ausgestreckten Finger und vier eingeknickte.
4. Nun wird vom Zehnfachen der Zahl der linken Hand das Produkt der ausgestreckten Finger abgezogen.

Beispiel: 3 mal 9

1. Die linke Hand streckt drei Finger aus.
2. Die rechte Hand zählt bis zur 9. Danach ist ein Finger dieser Hand ausgestreckt.
3. Die Zahl der ausgestreckten Finger der linken Hand beträgt 3, also ist 30 der Summand des Zwischenergebnisses.
4. Danach wird 3 × 1 gerechnet, also 3, und davon abgezogen.
5. 30 - 3 = 3 × 9 = 27

Beweis:

Wenn

• a = Zahl der ausgestreckten Finger der linken Hand
• b = Zahl der ausgestreckten Finger der rechten Hand

dann gilt

• $10 \cdot a - a \cdot b = a \cdot ({\color{Red}10} - b)$

(C) Multiplikation zweier Faktoren, beide über 5

Diese Methode ist älter als Anna Schnasing. So wird sie unter anderem von dem persischen Schriftsteller Beha Ad-Din Al'Amuli beschrieben, der sich Ende des 16. und im frühen 17. Jahrhundert mit Algebra befasste. Heute ist er unter anderem noch bekannt, weil er einen Spezialfall von Fermats letztem Satz behandelte. Auch der französische Mathematiker Nicolas Chuquet geht in Triparty en la science des Nombres auf diese Art der Multiplikation ein. ^[1]

Die Methode könnte Anna von einem Unbekannten beigebracht worden sein, als sie zu Hause im Spreewald war und von ihrem Ärger mit unehrlichen Kunden berichtete.

1. Beide geschlossene Fäuste werden vor den Körper gehalten.
2. Die linke Hand streckt so viele Finger aus, wie die Zahl eines Faktors ist, knickt aber ab 6 die Finger wieder ein. Die 9 hat beispielsweise einen ausgestreckten Finger und vier eingeknickte.
3. Die rechte Hand macht das mit dem zweiten Faktor genau so.
4. Nun werden alle eingeknickten Finger beider Hände gezählt und als 10er gemerkt (erster Summand im Zwischenergebnis).
5. Mit den übrigen, ausgestreckten Fingern wird wie nach (A) verfahren (zweiter Summand im Zwischenergebnis).
6. Die Summanden beider Zwischenergebnisse werden addiert, man erhält das Ergebnis

Beispiel: 9 mal 8

1. Die linke Hand zählt bis zur 9. Danach ist ein Finger dieser Hand ausgestreckt.
2. Die rechte Hand zählt bis zur 8. Danach sind zwei Finger dieser Hand ausgestreckt.
3. Die Zahl der geknickten Finger beider Hände beträgt 7, also 70 im Summanden des ersten Zwischenergebnisses.
4. Danach wird 1 × 2 gerechnet, also 2 im zweiten Zwischenergebnis.
5. 70 + 2 = 9 × 8 = 72

Beweis:

Wenn

• a = Zahl der eingezogenen Finger der linken Hand
• b = Zahl der eingezogenen Finger der rechten Hand

dann gilt

• $\begin{array}{lcl} (5 + a) \cdot (5 + b) & = & 25 + 5 (a+b) + ab\\ 10 \cdot (a + b) + (5 - a) \cdot (5 - b) & = & {\color{Red}10} (a+b) +25 {\color{Red}- 5 }(a+b) + ab \end{array}$

Für die Zuhilfenahme der Fußzehen gelten entsprechende Erweiterungen. Das Verfahren ist viel schneller zu erlernen als das kleine oder große Einmaleins.

Anna Schnasing

Anna Schnasing war eine von vielen Milchverkäuferinnen (sogn. „Bolle-Mädchen”) der Berliner Meierei C. Bolle im Besitz von Carl Bolle, die am Lützowufer, der damaligen Stadtgrenze angesiedelt war. Schnasing verkaufte vermutlich zwischen 1879 und 1883 frische Milch an Hausfrauen in der Innenstadt und wurde durch eine besondere Fingerfertigkeit bekannt.

„Anna aus dem Spreewald” sei ein munteres Mädchen gewesen, habe aber „schlecht multiplizieren können” oder „das kleine Einmaleins nur bis zur 5 beherrscht”, weshalb sie oft von Kunden betrogen worden sei^[2] und weniger Geld zurück zum Chef in die Meierei brachte. Nach einem Kurzurlaub zu Hause im Spreewald kam sie eines Tages zurück und verblüffte jeden mit einer undurchsichtigen, aber absolut unfehlbaren Fingerrechnung, mit der sie in kurzer Zeit Rechnungsbeträge multiplizieren und addieren konnte, ohne dass jemand verstand, wie sie es machte. Erst einer ihrer Kunden, ein zurückgezogen lebender Privatdozent und Mathematiker, kam durch allmähliche Beobachtung während des Verkaufsvorgangs hinter das Geheimnis von Anna und schrieb darüber einen Bericht, der unter dem humoristischen Titel „Algebraische Fingerfertigkeiten” publiziert wurde^[3] und im Bildungsbürgertum für ziemliche Erheiterung sorgte. Woher das Mädchen diese Fähigkeit hatte, wurde nie bekannt. Sicher ist, dass Anna später bei Bolle Karriere machte, in die Buchhaltung versetzt und zur Directrice befördert wurde. Ihr weiteres Schicksal ist nicht überliefert.

Volkstümliches

Die angeblich schlechten Rechenfähigkeiten der Milchmädchen dieser Zeit werden oft als Ursprung des Begriffs Milchmädchenrechnung gesehen, obwohl der heutige Begriff nichts mit schlechter Rechenfähigkeit zu tun hat, sondern mit dem meist erfolglosen Unterfangen, spekulative und noch nicht getätigte Erlöse bereits in neue Vorhaben verplanen zu wollen. Es gibt ältere historische Belege für diesen Begriff. Er geht nicht auf Anna Schnasing zurück.

Weblinks

• Fibonacci-Gesten
• Fingerrechnen bis 100

Literatur

• zu Anna Schnasing: Volker Wieprecht, Robert Skuppin: Berliner populäre Irrtümer
• „Zahlen bitte! Milchmädchenrechnung“, in: NZZ-Folio Nr. 5, Mai 1999

1. ↑ Ifrah, Georges: Universalgeschichte der Zahlen, 2. Auflage von 1991, Sonderausgabe 1998 Parkland Verlag, Köln
2. ↑ Wieprecht V., Skuppin R.: „Berliner populäre Irrtümer: Ein Lexikon“, Berlin, 2005, Seite 143 Google Books
3. ↑ medienwerkstatt-online.de - Bolle: eine Berliner Institution