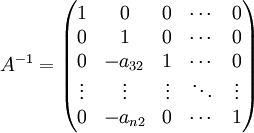Frobenius-Matrix

Eine Frobeniusmatrix ist eine spezielle Matrix aus dem mathematischen Teilgebiet der Numerik. Eine Matrix ist eine Frobeniusmatrix, wenn sie die folgenden drei Eigenschaften aufweist:

• auf der Hauptdiagonale stehen nur Einsen
• in höchstens einer Spalte stehen unter der Hauptdiagonale beliebige Einträge
• alle anderen Einträge sind Null

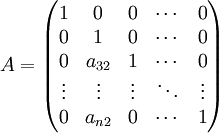
Ein Beispiel stellt die folgende Matrix dar.

$A=\begin{pmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & a_{32} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & a_{n2} & 0 & \cdots & 1 \end{pmatrix}$

Frobeniusmatrizen sind invertierbar. Ihre Inverse wird gebildet indem das Vorzeichen aller Einträge außerhalb der Hauptdiagonale gewechselt wird. Die Inverse des obigen Beispiels berechnet sich so zu:

$A^{-1}=\begin{pmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & -a_{32} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & -a_{n2} & 0 & \cdots & 1 \end{pmatrix}$

Die Frobeniusmatrizen sind nach Ferdinand Georg Frobenius benannt. Sie treten bei der Beschreibung des Gaußschen Eliminationsverfahren als Darstellungsmatrizen der Gauß-Transformationen auf.

Wird eine Matrix von links mit einer Frobeniusmatrix multipliziert, dann wird ein skalares Vielfaches einer bestimmten Zeile zu einer oder mehreren darunter liegenden Zeilen addiert. Die Multiplikation mit der Inversen einer Frobeniusmatrix ergibt die entsprechende Subtraktion von skalaren Vielfachen einer Zeile. Dies entspricht einer der Elementaroperationen des Gaußschen Eliminationsverfahrens (neben der Operation der Vertauschung von Zeilen und Multiplikation einer Zeile mit einem skalaren Vielfachen).

Quellen

• Josef Stoer: Einführung in die Numerische Mathematik 1. 9. Auflage. Springer-Verlag, 2005, ISBN 3-540-21395-3, S. 201