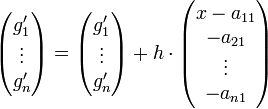- Frobenius-Normalform/Beweis der Isomorphieeigenschaft
-
Im Rahmen der Herleitung der Frobenius-Normalform ist zum Beweis der Isomorphieeigenschaft der Abbildung
zu zeigen,
- dass es sich um einen K[x]-Modul-Homomorphismus handelt, wenn links vom Gleichheitszeichen mit Vektoren statt mit Restklassen gerechnet wird
- dass die Summe rechts vom Gleichheitszeichen unverändert bleibt, wenn zum Vektor links vom Gleichheitszeichen ein Vektor aus M addiert wird (Wohldefiniertheit der Restklassenabbildung)
- dass jeder Vektor als Bild rechts vom Gleichheitszeichen auftauchen kann (Surjektivität)
- dass der Restklassenraum als K-Vektorraum keine größere Dimension als n hat (dann folgt zusammen mit den anderen Eigenschaften auch die Injektivität der Abbildung).
Inhaltsverzeichnis
Homomorphie
Die Homomorphie ergibt sich aus den Distributivgesetzen.
Wohldefiniertheit
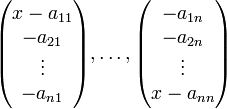
Jeder Vektor aus M ist Linearkombination der Spaltenvektoren
mit Koeffizienten in K[x]. Der j-te dieser Spaltenvektoren wird abgebildet auf
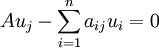 ,
,
also gilt dies wegen der Homomorphie für jeden Vektor aus M.
Surjektivität
Der erste Vektor der Standardbasis wird abgebildet auf
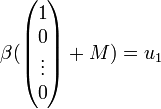 ,
,
analog der zweite Vektor der Standardbasis auf u2 usw., also wird jeder Basisvektor aus
 erreicht und wegen der Homomorphie damit jeder Vektor.
erreicht und wegen der Homomorphie damit jeder Vektor.Dimensionsgleichheit
Nach evtl. Umnummerierung können wir annehmen, dass die Komponenten des Vektors
nach Polynomgraden absteigend geordnet sind. Das Polynom g1 vom höchsten Grad d lässt sich durch Addition eines in M gelegenen K[x]-Vielfachen ersten Spalte von xE − A in den Vektor
mit
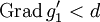 überführen, wobei
überführen, wobei ![h\in K[x]](/pictures/dewiki/49/1e3df9381cfe6bde42cbdf746cb3e286.png) einen Grad < d hat, und also für die übrigen Komponenten entweder
einen Grad < d hat, und also für die übrigen Komponenten entweder 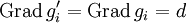 gilt oder
gilt oder 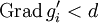 , wenn auch
, wenn auch 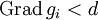 war. Durch wiederholtes Addieren von Vektoren aus M lässt sich also der jeweils höchste Grad reduzieren, bis schließlich alle Komponenten Grad 0 haben. Modulo M bilden daher die n Spalten der Einheitsmatrix E ein K-Erzeugendensystem des Restklassenraumes, der daher als K-Vektorraum höchstens Dimension n haben kann.
war. Durch wiederholtes Addieren von Vektoren aus M lässt sich also der jeweils höchste Grad reduzieren, bis schließlich alle Komponenten Grad 0 haben. Modulo M bilden daher die n Spalten der Einheitsmatrix E ein K-Erzeugendensystem des Restklassenraumes, der daher als K-Vektorraum höchstens Dimension n haben kann.
Wikimedia Foundation.

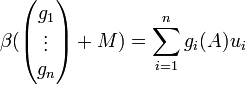
![\begin{pmatrix}g_1\\ \vdots \\g_n\end{pmatrix}\in K[x]^n](/pictures/dewiki/54/6207007152097a1b80c2d2bb2569cae1.png)