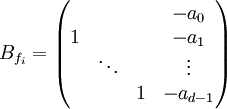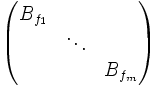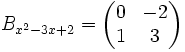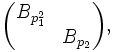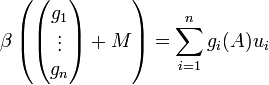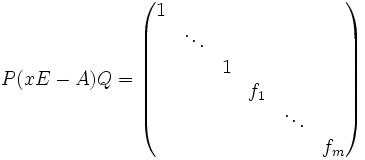- Rationale Normalform
-
Die Frobenius-Normalform (nach Ferdinand Georg Frobenius) einer quadratischen Matrix A mit Einträgen in einem beliebigen Körper K ist eine transformierte Matrix T − 1AT (mit invertierbarer Matrix T), die eine spezielle übersichtliche Form hat. "Übersichtlich" deswegen, weil sich jede Matrix in genau eine Matrix dieser Form transformieren lässt, und sich zwei Matrizen daher genau dann in einander transformieren lassen, wenn sie dieselbe Frobenius-Normalform haben. Wenn das der Fall ist, sagt man auch, die zwei Matrizen seien sich ähnlich, weil sie dieselbe lineare Abbildung bezüglich unterschiedlicher Basen darstellen. Zu jeder linearen Abbildung eines endlich-dimensionalen Vektorraums in sich gibt es daher eine Basis, bezüglich derer sie in Frobenius-Normalform dargestellt wird. Es kann mehrere solche Basen geben, die Transformationsmatrix T ist also nicht eindeutig bestimmt.
Die Frobenius-Normalform lässt sich einerseits als Alternative zur jordanschen Normalform auffassen (die ihrerseits eine Verallgemeinerung der Diagonalform ist), wobei nicht mehr vorausgesetzt werden muss, dass das charakteristische Polynom in Linearfaktoren zerfällt. Andererseits charakterisiert das Lemma von Frobenius zueinander ähnliche Matrizen durch die Elementarteiler ihrer charakteristischen Matrizen und liefert die Frobenius-Normalform als Normalform des Vektorraums unter der Operation eines Polynomrings.
Verallgemeinerung der Diagonalisierung
Wenn eine Matrix
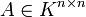 diagonalisierbar ist, zerfällt ihr charakteristisches Polynom f(x) = det(xE − A) in lauter Linearfaktoren
diagonalisierbar ist, zerfällt ihr charakteristisches Polynom f(x) = det(xE − A) in lauter Linearfaktoren  mit Eigenwerten
mit Eigenwerten 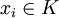 . Die zugehörigen Eigenvektoren vi mit (A − xiE)vi = 0 bilden eine Basis des Vektorraums Kn, in der jeder Basisvektor durch A auf ein Vielfaches von sich abgebildet wird.
. Die zugehörigen Eigenvektoren vi mit (A − xiE)vi = 0 bilden eine Basis des Vektorraums Kn, in der jeder Basisvektor durch A auf ein Vielfaches von sich abgebildet wird.Bei einer nicht diagonalisierbaren Matrix A sind nicht genügend Eigenvektoren für eine Basis vorhanden, oder das charakteristische Polynom
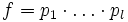 zerfällt in irreduzible Faktoren pi, die nicht alle Grad 1 haben. Zur Ermittlung der Frobenius-Normalform von A wird dann analog zum letzten Absatz eine Basis aus Vektoren gesucht, die von bestimmten Produkten der irreduziblen Faktoren
zerfällt in irreduzible Faktoren pi, die nicht alle Grad 1 haben. Zur Ermittlung der Frobenius-Normalform von A wird dann analog zum letzten Absatz eine Basis aus Vektoren gesucht, die von bestimmten Produkten der irreduziblen Faktoren 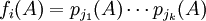 etc. zu null gemacht werden. Es zeigt sich, dass dies möglich ist und man schließlich eine Darstellung
etc. zu null gemacht werden. Es zeigt sich, dass dies möglich ist und man schließlich eine Darstellung  erhält, in der f1 Teiler von f2 ist, f2 Teiler von f3 usw. Zum Faktor
erhält, in der f1 Teiler von f2 ist, f2 Teiler von f3 usw. Zum Faktor 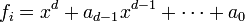 gehören dabei die Basisvektoren
gehören dabei die Basisvektoren  , deren Teilraum wegen
, deren Teilraum wegen 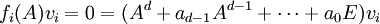 von A in sich abgebildet wird und auf dem A bezüglich dieser Basisvektoren durch die Matrix
von A in sich abgebildet wird und auf dem A bezüglich dieser Basisvektoren durch die Matrixdargestellt wird (die nicht angegebenen Einträge in dieser sog. Begleitmatrix zum Polynom fi sind 0). Der gesamte Vektorraum Kn zerfällt in solche A-invarianten Teilräume, und A lässt sich insgesamt durch die Blockdiagonalmatrix
darstellen. Sie ist die Frobenius-Normalform von A.
Ein Nachteil dabei ist, dass die Frobenius-Normalform einer Diagonalmatrix mit Eigenwerten 1 und 2 nicht Diagonalform hat, sondern
ist. Abhilfe schafft hier die Weierstraß-Normalform, in der die Begleitmatrix
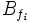 in der Blockdiagonalmatrix ersetzt wird durch die Begleitmatrizen der Potenzen verschiedener irreduzibler Faktoren von fi, also etwa durch
in der Blockdiagonalmatrix ersetzt wird durch die Begleitmatrizen der Potenzen verschiedener irreduzibler Faktoren von fi, also etwa durchfalls
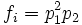 mit
mit 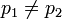 . Eine Matrix ist genau dann diagonalisierbar, wenn alle diese Faktoren linear sind und keiner in zweiter oder höherer Potenz vorkommt; also ist dann auch ihre Weierstraß-Normalform eine Diagonalmatrix.
. Eine Matrix ist genau dann diagonalisierbar, wenn alle diese Faktoren linear sind und keiner in zweiter oder höherer Potenz vorkommt; also ist dann auch ihre Weierstraß-Normalform eine Diagonalmatrix.Lemma von Frobenius
Die Menge aller Polynome, das sind Ausdrücke der Form
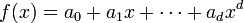 , mit Koeffizienten
, mit Koeffizienten 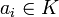 , bildet einen Ring, den sog. Polynomring K[x]. Wenn eine Matrix
, bildet einen Ring, den sog. Polynomring K[x]. Wenn eine Matrix 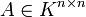 vorgegeben ist, kann man ein Produkt aus Polynom und Vektor
vorgegeben ist, kann man ein Produkt aus Polynom und Vektor 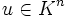 definieren durch
definieren durch 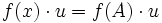 , für das die erwarteten Assoziativ- und Distributivgesetze gelten. Man spricht von einer Operation des Polynomrings auf dem Vektorraum, durch die der Vektorraum Kn zu einem K[x]-Modul wird.
, für das die erwarteten Assoziativ- und Distributivgesetze gelten. Man spricht von einer Operation des Polynomrings auf dem Vektorraum, durch die der Vektorraum Kn zu einem K[x]-Modul wird.Nach Wahl einer Basis
 von Kn kann man einen K[x]-Modul-Isomorphismus β angeben zwischen dem Faktormodul K[x]n modulo dem Erzeugnis M der Spalten der charakteristischen Matrix xE − A einerseits und Kn andererseits. Dieser Isomorphismus überträgt die Operation des Polynomrings (β(hg + M) = hβ(g + M) für
von Kn kann man einen K[x]-Modul-Isomorphismus β angeben zwischen dem Faktormodul K[x]n modulo dem Erzeugnis M der Spalten der charakteristischen Matrix xE − A einerseits und Kn andererseits. Dieser Isomorphismus überträgt die Operation des Polynomrings (β(hg + M) = hβ(g + M) für ![h\in K[x]](/pictures/dewiki/49/1e3df9381cfe6bde42cbdf746cb3e286.png) ,
, ![g\in K[x]^n](/pictures/dewiki/55/79963f215e1f6ae13dfee05fa49fb83d.png) ) und ist definiert durch
) und ist definiert durch(zum Beweis der Isomorphieeigenschaft siehe hier).
Die charakteristische Matrix
![xE-A \in K[x]^{n\times n}](/pictures/dewiki/99/c3a05e7bb978bfc82a2425808d364500.png) mit Einträgen im Polynomring kann durch den Elementarteileralgorithmus in eine Matrix
mit Einträgen im Polynomring kann durch den Elementarteileralgorithmus in eine Matrixmit invertierbaren
![P,Q\in K[x]^{n\times n}](/pictures/dewiki/51/3feaca3d3482dd75cf0362bc0b80c7b8.png) überführt werden, wobei f1 Teiler von f2 ist, f2 Teiler von f3 usw. und
überführt werden, wobei f1 Teiler von f2 ist, f2 Teiler von f3 usw. und  (die Polynome fi heißen die Elementarteiler der Matrix). Wegen der Invertierbarkeit von P und Q ist Kn dann auch isomorph zum Faktormodul K[x]n modulo dem Erzeugnis der Spalten von P(xE − A)Q und dieser Faktormodul zerfällt als direkte Summe
(die Polynome fi heißen die Elementarteiler der Matrix). Wegen der Invertierbarkeit von P und Q ist Kn dann auch isomorph zum Faktormodul K[x]n modulo dem Erzeugnis der Spalten von P(xE − A)Q und dieser Faktormodul zerfällt als direkte Summe ![K[x]/f_1K[x] \oplus \cdots \oplus K[x]/f_mK[x]](/pictures/dewiki/50/21f6652d6cfe1175e409cfc20f56b9da.png) . Die Operation des Polynoms x auf dem direkten Summanden K[x] / fiK[x] wird, wenn eine Basis
. Die Operation des Polynoms x auf dem direkten Summanden K[x] / fiK[x] wird, wenn eine Basis 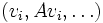 wie im vorigen Abschnitt gewählt wird, durch die Begleitmatrix
wie im vorigen Abschnitt gewählt wird, durch die Begleitmatrix 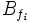 dargestellt, so dass sich für die Operation von x bzw. A auf dem ganzen Vektorraum die Frobenius-Normalform ergibt.
dargestellt, so dass sich für die Operation von x bzw. A auf dem ganzen Vektorraum die Frobenius-Normalform ergibt.Die Aussage, dass zwei Matrizen genau dann einander ähnlich sind, wenn ihre charakteristischen Matrizen dieselben Elementarteiler haben, heißt Lemma von Frobenius.
Als weitere Folgerung aus dem Gezeigten ergibt sich der Satz von Cayley-Hamilton: Die Operation des charakteristischen Polynoms f macht alle direkten Summanden K[x] / fiK[x] zu null, weil alle fi Teiler von f sind. Deswegen ist f(A) = 0, also ergibt eine Matrix, in ihr charakteristisches Polynom eingesetzt, die Nullabbildung.
Weblinks
- Vorlesungsmitschrift, Kapitel 2
Wikimedia Foundation.