Surjektivität

Eine surjektive Funktion; X ist die Definitionsmenge und Y die Zielmenge.

Surjektivität (surjektiv) oder Rechtstotalität (rechtstotal; in der Sprache der Relationen) ist eine Eigenschaft einer mathematischen Funktion. Sie bedeutet, dass jedes Element der Zielmenge mindestens einmal als Funktionswert angenommen wird, also mindestens ein Urbild hat. Eine Funktion ist bezüglich ihrer Bildmenge immer surjektiv. Eine surjektive Funktion wird auch als Surjektion bezeichnet.

Definition

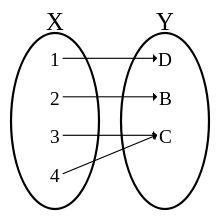
Es seien X und Y Mengen, sowie $f\colon\, X \to Y$ eine Abbildung.

f heißt surjektiv, wenn für alle y aus Y mindestens ein x aus X mit f(x) = y existiert.

Formal: $\forall y \in Y\colon \ \exists x \in X\colon\, f(x)=y$

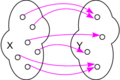
Grafische Veranschaulichungen

• 

  Das Prinzip der Surjektivität: Jeder Punkt in der Zielmenge (Y) wird mindestens einmal getroffen.

• 

  Graphen dreier surjektiver Funktionen zwischen reellen Intervallen.

• 

  Ein Sonderfall der Surjektivität: Die Zielmenge (Y) besteht nur aus einem Element.

Beispiele und Gegenbeispiele

• Die Funktion $f\colon\, \R \to \R$ mit f(x) = 2x + 1 ist surjektiv, denn für jede reelle Zahl y gibt es ein Urbild. Aus der Gleichung y = 2x + 1 erhält man nämlich durch Äquivalenzumformung die Gleichung x = (y − 1) / 2, womit sich für jedes y ein Urbild x berechnen lässt.

• Die Sinus-Funktion $\sin\colon\, \R \to [-1,1]$ ist surjektiv. Jede horizontale Gerade y = c mit $-1 \leq c \leq 1$ hat unendlich viele Schnittpunkte mit dem Graphen der Funktion.

• Die Sinus-Funktion $\sin\colon\, \R \to \R$ ist jedoch nicht surjektiv, da z. B. die Gerade y = 2 keinen Schnittpunkt mit dem Graphen hat, der Wert 2 also nicht als Funktionswert angenommen wird.

• $\C$ bezeichne die Menge der komplexen Zahlen.

$f_1\colon\, \R \rightarrow \R,\, x \mapsto x^2$ ist nicht surjektiv, da z. B. − 1 kein Urbild hat.

$f_2\colon\, \C \rightarrow \C,\, x \mapsto x^2$ ist surjektiv.

Eigenschaften

• Man beachte, dass die Surjektivität einer Funktion $f\colon\, A \to B$ nicht nur vom Funktionsgraphen $\{(x,f(x)) \mid x \in A\},$ sondern auch von der Zielmenge B abhängt (im Gegensatz zur Injektivität, welche man am Funktionsgraphen ablesen kann).

• Sind die Funktionen $f\colon\, A \to B$ und $g\colon\, B \to C$ surjektiv, dann gilt dies auch für die Komposition (Verkettung) $g \circ f\colon\, A \to C.$

• Aus der Surjektivität von $g \circ f$ folgt, dass g surjektiv ist.

• Eine Funktion $f\colon\, A \to B$ ist genau dann surjektiv, wenn f eine rechte Inverse hat, also eine Funktion $g\colon\, B \to A$ mit $f \circ g = \operatorname{id}_B$ (wobei $\operatorname{id}_B$ die identische Abbildung auf B bezeichnet). Diese Aussage ist äquivalent zum Auswahlaxiom der Mengenlehre.

• Eine Funktion $f\colon\, A \to B$ ist genau dann surjektiv, wenn $f\big(f^{-1}(Y) \big)=Y$ für alle $Y \subset B$.

• Eine Funktion $f : A \to B$ ist genau dann surjektiv, wenn f rechts kürzbar ist, also für beliebige Funktionen $g, h : B \to C$ mit $g \circ f = h \circ f$ schon g = h folgt. (Diese Eigenschaft motiviert den in der Kategorientheorie verwendeten Begriff Epimorphismus.)

• Jede beliebige Funktion $f\colon\, A \to B$ ist darstellbar als Verkettung $f = h \circ g$, wobei g surjektiv und h injektiv ist. $g\colon\, A \to \operatorname{im} f$ hat dabei die Bildmenge von f als Zielmenge und stimmt ansonsten mit f überein (hat denselben Funktionsgraphen).

Mächtigkeiten von Mengen

Für eine endliche Menge A ist die Mächtigkeit | A | einfach die Anzahl der Elemente von A. Ist nun $f\colon\, A \to B$ eine surjektive Funktion zwischen endlichen Mengen, dann kann B höchstens so viele Elemente wie A haben, es gilt also $|B| \le |A|.$

Für unendliche Mengen wird der Größenvergleich von Mächtigkeiten zwar mit Hilfe des Begriffs Injektion definiert, aber auch hier gilt: Ist $f\colon\, A \to B$ surjektiv, dann ist die Mächtigkeit von B kleiner oder gleich der Mächtigkeit von A, ebenfalls geschrieben als $|B| \le |A|.$

Siehe auch

• Bijektivität
• Injektivität
• Epimorphismus

Literatur

• O. A. Ivanova: Surjection. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics. Springer-Verlag, Berlin 2002, ISBN 1-4020-0609-8.

Weblinks

•  Wikibooks: Beweisarchiv: Mengenlehre – Lern- und Lehrmaterialien