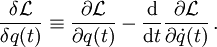- Gateaux-Differential
-
Das Gâteaux-Differential, benannt nach René Gâteaux (1889-1914), stellt eine Verallgemeinerung des gewöhnlichen Differentiationsbegriffes dar. Gewöhnlich hat man für eine Funktion
 offene Menge, die an der Stelle
offene Menge, die an der Stelle 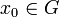 differenzierbar ist, als Definition der (partiellen) Ableitung
differenzierbar ist, als Definition der (partiellen) Ableitung 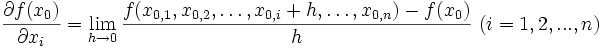 . Insbesondere ergibt sich für n = 1 das bekannte
. Insbesondere ergibt sich für n = 1 das bekannte  .
.Inhaltsverzeichnis
Definitionen
1. Variation; Variationsableitung
Sei nun für das Gâteaux-Differential folgende Situation gegeben: Es sei wie üblich
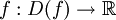 ein in
ein in 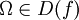 definiertes Funktional; Ω sei ein offener linearer normierter Raum (d. h. ein Vektorraum, versehen mit einer Norm
definiertes Funktional; Ω sei ein offener linearer normierter Raum (d. h. ein Vektorraum, versehen mit einer Norm  ) oder ein allgemeinerer topologischer Vektorraum mit Voraussetzungen, über die man sich im konkreten Anwendungsfall nähere Gedanken machen muss; ferner sei
) oder ein allgemeinerer topologischer Vektorraum mit Voraussetzungen, über die man sich im konkreten Anwendungsfall nähere Gedanken machen muss; ferner sei 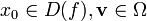 (also ein Vektor).
(also ein Vektor).Dann ist das Gâteaux-Differential an der Stelle x0, falls es dort existiert, definiert durch die folgende Ableitung nach ε:
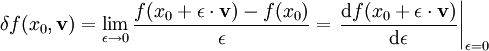
oder auch für
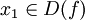 durch
durch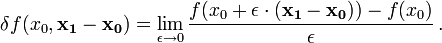
Man beachte dabei
 ,
, 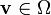 und ebenfalls
und ebenfalls 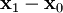 darin, aber
darin, aber 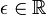 .
.Die Gâteaux-Ableitung nach ε ist bezüglich der Größe
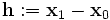 ein Funktional, das auch als 1. Variation von f an der Stelle x0 bezeichnet wird.
ein Funktional, das auch als 1. Variation von f an der Stelle x0 bezeichnet wird.Eine andere Möglichkeit ist, anstelle normierter Vektorräume allgemeinere topologische Vektorräume mit komplizierterem Konvergenzbegriff zu benutzen, z. B. Verallgemeinerte Funktionen (Distributionen) wie die Dirac-Funktion δ(x − a).
Vor allem in Physikbüchern werden Funktionale üblichweise mit dem Buchstaben „I“ bezeichnet, und statt der Größe
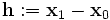 schreibt man meist
schreibt man meist 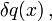 mit distributionswertigen Größen. Statt der Ableitung
mit distributionswertigen Größen. Statt der Ableitung 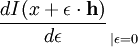 führt man in einem Zusatzschritt die sog. Variationsableitung ein, die eng mit der Gâteaux-Ableitung zusammenhängt.
führt man in einem Zusatzschritt die sog. Variationsableitung ein, die eng mit der Gâteaux-Ableitung zusammenhängt.Beispiel: Für
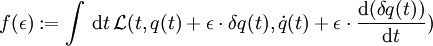 erhält man nach einer partiellen Integration mit verschwindendem ausintegrierten Teil ein Resultat der Form
erhält man nach einer partiellen Integration mit verschwindendem ausintegrierten Teil ein Resultat der Form 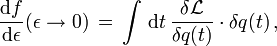 mit der Variationsableitung
mit der Variationsableitung(Die Variationsableitung "an der Stelle q(t)" bei kontinuierlichen Variablen ist also die Verallgemeinerung der partiellen Ableitung
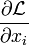 einer Funktion von n Variablen, also z. B. für den fiktiven Fall
einer Funktion von n Variablen, also z. B. für den fiktiven Fall 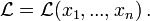 So ähnlich wie im fiktiven Fall das totale Differential einer Funktion von n Variablen, so hat auch hier
So ähnlich wie im fiktiven Fall das totale Differential einer Funktion von n Variablen, so hat auch hier 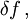 das totale Differential des Funktionals, invariante Bedeutung. Weitere Einzelheiten im Kapitel Lagrange-Formalismus.)
das totale Differential des Funktionals, invariante Bedeutung. Weitere Einzelheiten im Kapitel Lagrange-Formalismus.)In Folgenden wird der Einfachheit halber auf die Kennung der Vektoren durch „fett geschriebene“ Buchstaben verzichtet.
2. Variation
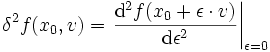
Halbseitiges Differential und Richtungsableitung
Unter denselben Voraussetzungen wie oben ist das einseitige Gâteaux-Differential definiert:
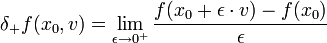 bzw.
bzw.  Das einseitige Gâteaux-Differential wird auch Richtungsdifferential von f an der Stelle x0 genannt. Für die zum Vektor v gehörende Richtung verallgemeinert nämlich bei „kontinuierlichen Variablen“ das einseitige Gâteaux-Differential (genauer: die zugehörige Variationsableitung) gerade die Richtungsableitung von f in Richtung v an der Stelle x0.
Das einseitige Gâteaux-Differential wird auch Richtungsdifferential von f an der Stelle x0 genannt. Für die zum Vektor v gehörende Richtung verallgemeinert nämlich bei „kontinuierlichen Variablen“ das einseitige Gâteaux-Differential (genauer: die zugehörige Variationsableitung) gerade die Richtungsableitung von f in Richtung v an der Stelle x0.Gâteaux-Ableitung
Ist δf(x0,v) ein in v stetiges, lineares Funktional (d. h. die Funktion vermittelt durch
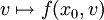 ist homogen, additiv und stetig im Argument v), dann heißt f'(x0) Gâteaux-Ableitung an der Stelle x0. und f Gâteaux-differenzierbar in x0.
ist homogen, additiv und stetig im Argument v), dann heißt f'(x0) Gâteaux-Ableitung an der Stelle x0. und f Gâteaux-differenzierbar in x0.Eigenschaften der 1. Variation
Homogenität
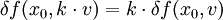 für alle
für alle 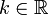
Die Eigenschaft gilt analog für das einseitige Gâteaux-Differential.
Beweis:
 (nun nennen wir
(nun nennen wir 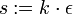 )
)  (und nun wieder ε = s)
(und nun wieder ε = s) 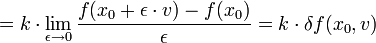
Nichtlinearität
Im allgemeinen Fall gilt
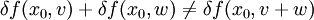 .
.Gegenbeispiel zur Linearität:
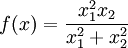 für
für  und f(0) = 0, wobei x = (x1,x2), dann ist
und f(0) = 0, wobei x = (x1,x2), dann ist 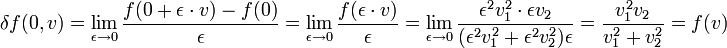 . Die Funktion f ist nicht linear. Es ist zum Beispiel
. Die Funktion f ist nicht linear. Es ist zum Beispiel 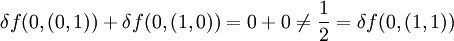 .
.Beispiele
- f(x1,x2) = 1, falls
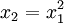 ,
, 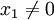 bzw 0 sonst
bzw 0 sonst 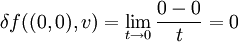 .
. 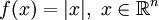
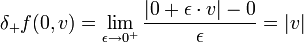
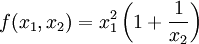 für
für 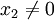 und
und  für x2 = 0,
für x2 = 0, 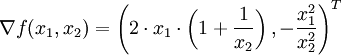
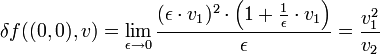 (wobei v = (v1,v2)T)
(wobei v = (v1,v2)T)Anwendungen
Wie die gewöhnliche Ableitung ist das Gâteaux-Differential zum Bestimmen von Extrema und daher in der Optimierung von Nutzen. Sei
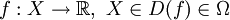 offen, Ω linearer normierter Raum,
offen, Ω linearer normierter Raum, 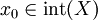 (das Innere der Menge X),
(das Innere der Menge X), 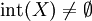 und
und  der offene Ball um x0 mit Radius
der offene Ball um x0 mit Radius  . Notwendige Optimalitätsbedingung: Sei x0 ein lokales Minimum von f auf X, dann ist
. Notwendige Optimalitätsbedingung: Sei x0 ein lokales Minimum von f auf X, dann ist 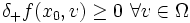 , falls das einseitige Gâteaux-Differential in x0 existiert. Hinreichende Optimalitätsbedingung: f besitze in
, falls das einseitige Gâteaux-Differential in x0 existiert. Hinreichende Optimalitätsbedingung: f besitze in  eine 2. Variation
eine 2. Variation 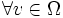 und
und  . Falls gilt
. Falls gilt 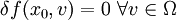 und für ein c > 0
und für ein c > 0 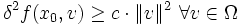 und
und  , dann ist x0 strenge lokale Minimalstelle von f auf
, dann ist x0 strenge lokale Minimalstelle von f auf  .
.Siehe auch
Wikimedia Foundation.