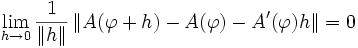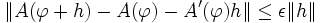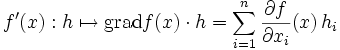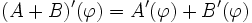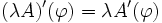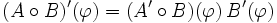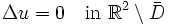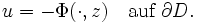- Fréchet-Differential
-
Die Fréchet-Ableitung (nach Maurice René Fréchet) verallgemeinert den Begriff der Ableitung aus der üblichen Differentialrechnung im
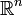 auf normierte Räume.
auf normierte Räume.Inhaltsverzeichnis
Definition
Es seien X und Y normierte Räume und
 eine offene Teilmenge. Ein Operator
eine offene Teilmenge. Ein Operator 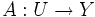 heißt Fréchet-differenzierbar an der Stelle
heißt Fréchet-differenzierbar an der Stelle 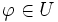 , wenn es einen beschränkten linearen Operator
, wenn es einen beschränkten linearen Operator 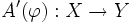 derart gibt, dass
derart gibt, dassgilt. Der Operator
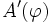 heißt Fréchet-Ableitung von A an der Stelle
heißt Fréchet-Ableitung von A an der Stelle 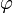 . Existiert die Fréchet-Ableitung für alle
. Existiert die Fréchet-Ableitung für alle 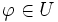 , dann heißt die Abbildung
, dann heißt die Abbildung 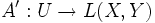 mit
mit 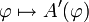 die Fréchet-Ableitung von A auf U.
die Fréchet-Ableitung von A auf U.Mit L(X,Y) bezeichnen wir hier den der Raum der stetigen linearen Abbildungen von X nach Y.
Äquivalente Definition
Eine äquivalente Definition ist:
Zu jedem ε > 0 gibt es ein δ > 0 so, dass
für alle
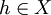 mit
mit 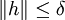 . Dies lässt sich auch kurz mit Hilfe der Landau-Symbole schreiben:
. Dies lässt sich auch kurz mit Hilfe der Landau-Symbole schreiben: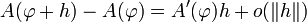 für
für 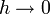 .
.
Beispiele
Lineare Operatoren
Für endlichdimensionale normierte Räume X,Y sind alle linearen Operatoren
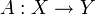 Fréchet-differenzierbar mit konstanter Ableitung. An jedem Punkt ist die Ableitung der lineare Operator selbst: A'(x) = A.
Fréchet-differenzierbar mit konstanter Ableitung. An jedem Punkt ist die Ableitung der lineare Operator selbst: A'(x) = A.Im unendlichdimensionalen Fall sind genau die beschränkten (=stetigen) linearen Operatoren Fréchet-differenzierbar. Unbeschränkte lineare Operatoren sind nicht Fréchet-differenzierbar.
Reellwertige Funktionen
Ist
 eine reellwertige Funktion, die auf einer offenen Menge
eine reellwertige Funktion, die auf einer offenen Menge 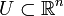 definiert ist und besitzt f stetige partielle Ableitungen, dann ist f auch Fréchet-differenzierbar. Die Ableitung an der Stelle x wird durch den üblichen Gradienten von f gegeben gemäß:
definiert ist und besitzt f stetige partielle Ableitungen, dann ist f auch Fréchet-differenzierbar. Die Ableitung an der Stelle x wird durch den üblichen Gradienten von f gegeben gemäß:Dieses Beispiel zeigt den Zusammenhang zur üblichen Differentialrechnung im
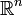 . Die Fréchet-Ableitung ist also tatsächlich eine Verallgemeinerung der Differentialrechnung für normierte Räume.
. Die Fréchet-Ableitung ist also tatsächlich eine Verallgemeinerung der Differentialrechnung für normierte Räume.Rechenregeln
Es lassen sich die üblichen Rechenregeln für die Ableitung im
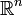 auch für die Fréchet-Ableitung zeigen. Es gilt:
auch für die Fréchet-Ableitung zeigen. Es gilt:Bei der letzten Regel (Kettenregel) müssen die Definitions- und Wertebereiche der Operatoren A und B übereinstimmen. Das Produkt
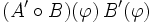 ist hierbei im Sinne der Multiplikation (Hintereinanderausführung) linearer Abbildungen zu verstehen.
ist hierbei im Sinne der Multiplikation (Hintereinanderausführung) linearer Abbildungen zu verstehen.Zusammenhang zwischen Fréchet- und Gâteaux-Ableitung
Sei A an der Stelle
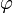 Fréchet-differenzierbar, dann existiert für jede beliebige Richtung
Fréchet-differenzierbar, dann existiert für jede beliebige Richtung 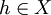 das Gâteaux-Differential
das Gâteaux-Differential 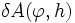 und es gilt:
und es gilt: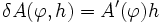 .
.
Die Umkehrung gilt im Allgemeinen nicht.
Außerdem existiert dann die Gâteaux-Ableitung von A an der Stelle
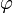 , die im Folgenden mit
, die im Folgenden mit  bezeichnet wird, und es gilt:
bezeichnet wird, und es gilt: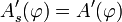 .
.
Auch hier gilt die Umkehrung im Allgemeinen nicht.
Unter folgenden Bedingungen gilt auch die Umkehrung:
Sei
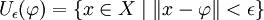 mit
mit  eine offene Kugel um den Punkt
eine offene Kugel um den Punkt 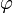 . Wenn
. Wenn 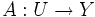 in jedem Punkt
in jedem Punkt 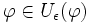 Gâteaux-differenzierbar ist und die Abbildung
Gâteaux-differenzierbar ist und die Abbildung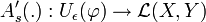 gegeben durch
gegeben durch 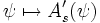
im Punkt
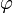 stetig ist, dann ist A im Punkt
stetig ist, dann ist A im Punkt 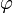 Fréchet-differenzierbar und es gilt:
Fréchet-differenzierbar und es gilt: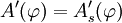 .
.
Anwendungsbeispiel
Die Fréchet-Ableitung kann z. B. zur Lösung sogenannter inverser Randwertprobleme im Rahmen eines Newton-Verfahrens verwendet werden. Als Beispiel für diese Anwendung betrachten wir ein inverses Randwertproblem zur Laplace-Gleichung:
Es sei
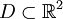 ein unbekanntes Gebiet. Wir betrachten das äußere Dirichlet-Problem, bei dem die Randwerte auf
ein unbekanntes Gebiet. Wir betrachten das äußere Dirichlet-Problem, bei dem die Randwerte auf 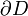 durch eine Quelle im Punkt
durch eine Quelle im Punkt 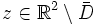 gegeben sind. Dann erfüllt die beschränkte und zweimal stetig differenzierbare Funktion u in
gegeben sind. Dann erfüllt die beschränkte und zweimal stetig differenzierbare Funktion u in 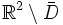 die Laplace-Gleichung:
die Laplace-Gleichung:und die Dirichlet Randbedingung:
Mit Φ bezeichnen wir die Grundlösung zur Laplace-Gleichung, die eine Punktquelle im Punkt z beschreibt.
Beim inversen Randwertproblem gehen wir von einem zweiten (bekannten) Gebiet
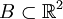 aus, welches D enthält. Auf dem Rand
aus, welches D enthält. Auf dem Rand 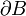 von B messen wir die Werte der Lösung u des direkten Dirichlet-Problems. Wir kennen also die Spur
von B messen wir die Werte der Lösung u des direkten Dirichlet-Problems. Wir kennen also die Spur 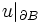 . Unser Ziel ist nun den unbekannten Rand
. Unser Ziel ist nun den unbekannten Rand 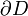 von D aus der Kenntnis dieser Spur zu rekonstruieren.
von D aus der Kenntnis dieser Spur zu rekonstruieren.Dieses Problem lässt sich formal durch einen Operator F beschreiben, der den unbekannten Rand
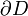 auf die bekannte Spur
auf die bekannte Spur 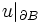 abbildet. Wir müssen also folgende nichtlineare Gleichung lösen:
abbildet. Wir müssen also folgende nichtlineare Gleichung lösen:Diese Gleichung kann z. B. mit Hilfe des Newton-Verfahrens linearisiert werden. Dazu schränken wir uns auf Gebiete D ein, dessen Rand wie folgt dargestellt werden kann:
Wir suchen nun also die unbekannte Radiusfunktion r. Die linearisierte Gleichung (das Newton-Verfahren) sieht dann wie folgt aus:
Hierbei bezeichnet
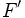 die Fréchet-Ableitung des Operators
die Fréchet-Ableitung des Operators 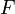 (Die Existenz der Fréchet-Ableitung für
(Die Existenz der Fréchet-Ableitung für 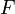 kann gezeigt werden und
kann gezeigt werden und 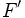 kann über ein direktes Randwertproblem bestimmt werden!). Diese Gleichung wird dann nach q aufgelöst, wobei wir mit r + q eine neue Näherung an den unbekannten gesuchten Rand gefunden haben. Anschließend kann mit dieser Näherung das Verfahren iteriert werden.
kann über ein direktes Randwertproblem bestimmt werden!). Diese Gleichung wird dann nach q aufgelöst, wobei wir mit r + q eine neue Näherung an den unbekannten gesuchten Rand gefunden haben. Anschließend kann mit dieser Näherung das Verfahren iteriert werden.Literatur
- Rainer Kress: Linear Integral Equations. Second Edition. Springer 1998, ISBN 0-387-98700-2
- Harro Heuser: Lehrbuch der Analysis – Teil 2. Teubner, Stuttgart – Leipzig, ISBN 3-519-42232-8
Siehe auch
Wikimedia Foundation.