Imaginäre Einheit — Darstellung einer komplexen Zahl in der Gaußebene In der Mathematik ist eine imaginäre Zahl eine Zahl, deren Quadrat eine negative reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. In seinen Augen konnten solche Zahlen… … Deutsch Wikipedia
Imaginäre Zahlen — Darstellung einer komplexen Zahl in der Gaußebene In der Mathematik ist eine imaginäre Zahl eine Zahl, deren Quadrat eine negative reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. In seinen Augen konnten solche Zahlen… … Deutsch Wikipedia
Gaußsche Zahlenebene — Darstellung einer komplexen Zahl in der Gaußschen Ebene Die gaußsche Zahlenebene (oder kurz Gaußebene) stellt eine geometrische Interpretation der komplexen Zahlen dar, die von Carl Friedrich Gauß um 1811 eingeführt wurde (er erwähnt die… … Deutsch Wikipedia
Imaginäre Zahl — Eine imaginäre Zahl ist eine Zahl, deren Quadrat eine nicht positive reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. Nach seiner Ansicht konnten solche Zahlen nicht existieren, sie konnten also nur imaginär (eingebildet)… … Deutsch Wikipedia
Arganddiagramm — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Gauß'sche Zahlenebene — Darstellung einer komplexen Zahl in der Gaußschen Ebene Als gaußsche Zahlenebene (nach Carl Friedrich Gauß) wird diejenige Menge aller 2 Tupel bezeichnet, welche aus der Zuordnung von imaginären zu reellen Zahlen entsteht. Der Begriff bezieht… … Deutsch Wikipedia
Gauß-Ebene — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Gaußsche Ebene — Darstellung einer komplexen Zahl in der Gaußschen Ebene Als gaußsche Zahlenebene (nach Carl Friedrich Gauß) wird diejenige Menge aller 2 Tupel bezeichnet, welche aus der Zuordnung von imaginären zu reellen Zahlen entsteht. Der Begriff bezieht… … Deutsch Wikipedia
Imaginärteil — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Irreelle Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
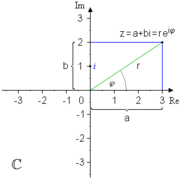Darstellung einer komplexen Zahl in der Gaußschen Ebene
bekannt ist. Topologisch lässt sich diese Menge als zweidimensionaler Vektorraum beschreiben, daher die Bezeichnung als Ebene. Dargestellt wird die Gaußebene als kartesisches Koordinatensystem mit dem reellen Zahlenstrahl als Abszisse und der axis imaginaera als Ordinate.
