gaußsche Zahlenebene — gaußsche Zahlen|ebene, gaußsche Ebene [nach C. F. Gauß], Ebene, in der jeder Punkt mit den kartesischen Koordinaten x, y durch die eindeutige Zuordnung (x, y) ↔ x + i … Universal-Lexikon
Gaußsche Zahlen — als Gitterpunkte in der komplexen Zahlenebene Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe … Deutsch Wikipedia
Gaußsche ganze Zahlen — Gaußsche Zahlen als Gitterpunkte in der komplexen Zahlenebene Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe … Deutsch Wikipedia
Gaußsche Zahl — Gaußsche Zahlen als Gitterpunkte in der komplexen Zahlenebene Die gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe Adju … Deutsch Wikipedia
gaußsche Abbildung — [nach C. F. Gauß], Optik: die ideale, d. h. fehlerfreie optische Abbildung, bei der durch die in Form gebrochener linearer Transformationen der Koordinaten (Kollineationen) gegebenen Abbildungsgleichungen alle Geraden und Ebenen des Ding oder… … Universal-Lexikon
gaußsche Koordinaten — [nach C. F. Gauß], rechtwinklige Koordinaten einer konformen Abbildung des Erdellipsoids in die Ebene, wobei ein Hauptmeridian als im Allgemeinen längentreue Abszissenachse abgebildet wird. Die Abbildung wurde von C. F. Gauß anlässlich der… … Universal-Lexikon
Gaußsche Krümmung — In der Theorie der Flächen im dreidimensionalen euklidischen Raum ( ), einem Gebiet der Differentialgeometrie, ist die gaußsche Krümmung (das gaußsche Krümmungsmaß), benannt nach dem Mathematiker Carl Friedrich Gauß, der wichtigste… … Deutsch Wikipedia
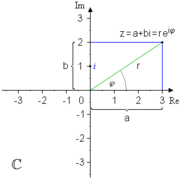
Gaußsche Zahlenebene — Darstellung einer komplexen Zahl in der Gaußschen Ebene Die gaußsche Zahlenebene (oder kurz Gaußebene) stellt eine geometrische Interpretation der komplexen Zahlen dar, die von Carl Friedrich Gauß um 1811 eingeführt wurde (er erwähnt die… … Deutsch Wikipedia
Ebene (Mathematik) — Die 3 Koordinatenebenen Die Ebene ist ein Grundbegriff der Geometrie. Allgemein handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt. Hierbei bedeutet unbegrenzt ausgedehnt und flach, dass zu je zwei Punkten auch eine… … Deutsch Wikipedia
Gaußsche Trapezformel — Mit Hilfe der gaußschen Trapezformel (nach Carl Friedrich Gauß) ist es möglich, die Fläche zwischen mehreren auf eine Messungslinie bezogenen/koordinierten Punkten, also beispielsweise die Fläche eines einfachen Polygons, zu berechnen. Durch die… … Deutsch Wikipedia
Darstellung einer komplexen Zahl in der Gaußschen Ebene
bekannt ist. Topologisch lässt sich diese Menge als zweidimensionaler Vektorraum beschreiben, daher die Bezeichnung als Ebene. Dargestellt wird die Gaußebene als kartesisches Koordinatensystem mit dem reellen Zahlenstrahl als Abszisse und der axis imaginaera als Ordinate.
