Gaußklammer

Die Gaußklammer oder Abrundungsfunktion (auch Ganzzahl-Funktion, Ganzteilfunktion oder Entier-Klammer; engl. floor function) und die Aufrundungsfunktion (engl. ceiling function) sind Funktionen, die einer reellen Zahl die nächstgrößere bzw. nächstkleinere ganze Zahl zuordnen. Die Notation wurde nach Carl Friedrich Gauß benannt, der das Symbol $\left[ x \right]$ für die Abrundungsfunktion 1808 eingeführt hat.^[1] Ende des 20. Jahrhunderts verbreiteten sich auch die von Kenneth E. Iverson eingeführten Bezeichnungen $\operatorname{floor}(x)$ und $\lfloor x \rfloor$ (engl. Fußboden) für die Gaußklammer sowie $\operatorname{ceil}(x)$ und $\lceil x \rceil$ (engl. ceiling: Decke) für die Aufrundungsfunktion.^[2]

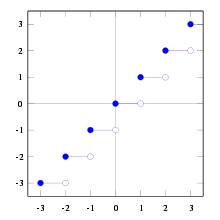
Die Abrundungsfunktion oder Gaußklammer

Gaußklammerfunktion oder Abrundungsfunktion

Definition

Sie ist folgendermaßen definiert:

Für eine reelle Zahl x ist $\lfloor x \rfloor$ die größte ganze Zahl, die kleiner oder gleich x ist:

$\lfloor x \rfloor=\max_{k\in\Z, k\leq x}k$

Beispiele

• $\lfloor 2{,}8 \rfloor = 2$

• $\lfloor -2{,}8 \rfloor = -3$

Man beachte, dass $\lfloor -2{,}8 \rfloor$ nicht etwa gleich − 2 ist. Die Definition verlangt ja $\lfloor x \rfloor \le x$, und es ist − 2 > − 2,8.

• $\lfloor 2 \rfloor = 2$

Eigenschaften

• Es gilt immer $\lfloor x \rfloor \le x < \lfloor x \rfloor+1$. Dabei ist $\lfloor x \rfloor = x$ genau dann, wenn x eine ganze Zahl ist.

• Für jede ganze Zahl k und jede reelle Zahl x gilt

$\lfloor x+k \rfloor = \lfloor x \rfloor + k$.

• Für alle reellen Zahlen x,y gilt

$\lfloor x \rfloor + \lfloor y \rfloor \le \lfloor x+y \rfloor \le \lfloor x \rfloor + \lfloor y \rfloor + 1$.

• Für jede ganze Zahl k und jede natürliche Zahl n gilt

$\left\lfloor \frac{k}{n} \right\rfloor \ge \frac{k-n+1}{n}$.

• Die Abrundungsfunktion ist idempotent: Es gilt

$\bigl\lfloor \lfloor x \rfloor \bigr\rfloor = \lfloor x \rfloor$.

• Sind m und n teilerfremde natürliche Zahlen, dann gilt

$\sum_{j=1}^{n-1} \left \lfloor \frac{jm}{n} \right \rfloor = \frac{(m-1)(n-1)}{2}$.

• Die Abrundungsfunktion ist nicht stetig, aber oberhalbstetig.

• Für nichtganze reelle x konvergiert die Fourierreihe der 1-periodischen Funktion $\lfloor x \rfloor-x$, und es gilt

$\lfloor x \rfloor = x-\frac{1}{2}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{\sin{(2k\pi x)}}{k}$.

Aufrundungsfunktion

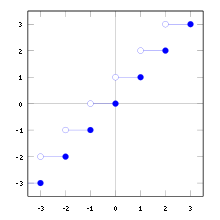
Aufrundungsfunktion

Definition

Sie ist so definiert:

Für eine reelle Zahl x ist $\lceil x \rceil$ die kleinste ganze Zahl, die größer oder gleich x ist.

$\lceil x \rceil:=\min_{k\in\Z, k\ge x}(k)$

Beispiele

• $\lceil 2{,}8 \rceil = 3$

• $\lceil -2{,}8 \rceil = -2$

• $\lceil 2 \rceil = 2$

Eigenschaften

• Es gilt analog

$\lceil \lceil x \rceil \rceil = \lceil x \rceil$

Allgemeine Eigenschaften

Gaußklammer und Dezimalstellen

Es gilt für positive Zahlen:

$x = \operatorname{floor}(x) + \operatorname{frac} (x)$

Die Funktion frac(x) liefert dabei den Nachkommaanteil der Zahl.

Zusammenhänge zwischen Auf- und Abrundungsfunktion

• Es ist stets

$\lceil x \rceil + \lfloor -x \rfloor = 0$

Deshalb erhält man die Aufrundungsfunktion aus der Gaußklammerfunktion per

$\lceil x \rceil = -\lfloor -x \rfloor$

• Für ganze Zahlen k gilt:

$\left\lfloor \frac{k}{2} \right\rfloor + \left\lceil \frac{k}{2} \right\rceil = k$

Kaufmännische Rundung

Die kaufmännische Rundung auf die nächstliegende ganze Zahl kann auch mit diesen Funktionen ausgedrückt werden:

• $\lfloor x + 0{,}5\rfloor \mbox{ für } x \ge 0$

• $\lceil x - 0{,}5\rceil \mbox{ für } x< 0$

Weblinks

• Eric W. Weisstein: Floor Function. In: MathWorld. (englisch)
• Eric W. Weisstein: Ceiling Function. In: MathWorld. (englisch)

Einzelnachweise

1. ↑ Earliest Uses of Function Symbols: Until recently [x] has been the standard symbol for the greatest integer function. According to Grinstein (1970), "The use of the bracket notation, which has led some authors to term this the bracket function, stems back to the work of Gauss (1808) in number theory. The function is also referred to by Legendre who used the now obsolete notation E(x)." The Gauss reference is to Theorematis arithmetici demonstratio nova. Werke Volume: Bd. 2 p. 5. (aufgerufen am 25. Juli 2009)
2. ↑ Earliest Known Uses of Some of the Words of Mathematics (C): The terms CEILING FUNCTION and FLOOR FUNCTION appear in Kenneth E. Iverson's A Programming Language (1962, p. 12): "Two functions are defined: 1. the floor of x (or integral part of x) denoted by $\lfloor x \rfloor$ and defined as the largest integer not exceeding x, 2. the ceiling of x denoted by $\lceil x \rceil$ and defined as the smallest integer not exceeded by x." This was the first appearance of the terms and symbols, according to R. L. Graham, D. E. Knuth & O. Patashnik Concrete Mathematics: A Foundation for Computer Science (1989, p. 67). (aufgerufen am 25. Juli 2009)