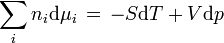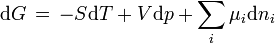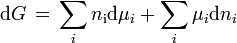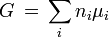Gibbs-Duhem-Beziehung

Die Gibbs-Duhem-Gleichung (nach Josiah Willard Gibbs und Pierre Duhem) beschreibt den Zusammenhang zwischen den Änderungen der chemischen Potentiale der Komponenten i eines thermodynamischen Systems.

Das als Gibbs-Duhem-Gleichung bezeichnete vollständige Differential des chemischen Potentials,

$\sum_i n_i \mathrm d \mu_i \,=\,- S \mathrm dT + V \mathrm dp$

folgt durch Vergleich des vollständigen Differentials des Gibbs-Potentials (freien Enthalpie) G,

$\mathrm dG \,=\, - S \mathrm dT + V \mathrm dp + \sum_i \mu_i \mathrm dn_i$

mit

$\mathrm dG \,=\, \sum_i n_\mathrm i \mathrm d \mu_i + \sum_i \mu_i \mathrm dn_i$

dem vollständigen Differential von

$G \,=\, \sum_i n_i \mu_i$

Die Gibbs-Duhem-Gleichung ist von großem Interesse für die Thermodynamik, da sie aufzeigt, dass in einem thermodynamischen System nicht alle intensiven Variablen (Variablen, die nicht von der Menge einer Substanz abhängen, wie z. B. Temperatur, Druck, Dichte, etc.) unabhängig voneinander veränderlich sind. Nimmt man die Temperatur T und den Druck p als veränderlich an, so können nur noch i − 1 der i Komponenten voneinander unabhängige chemische Potentiale aufweisen. Hieraus folgt die Gibbs'sche Phasenregel, die die Anzahl der möglichen Freiheitsgrade für dieses System angibt.

Oft wird die Gibbs-Duhem-Gleichung bei isothermer, isobarer Prozessführung verwendet. Es folgt dann

∑	nidμi = 0
i

Die Summe der Produkte aus der Veränderung des chemischen Potenzials μ_i und der Stoffmenge n_i der einzelnen Komponenten ist also bei einem solchen Prozess konstant.