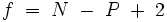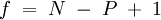Gibbsches Gesetz

Die Gibbssche Phasenregel (nach Josiah Willard Gibbs 1876) beinhaltet die Aussage, dass im thermodynamischen Gleichgewicht nicht beliebig viele Phasen gleichzeitig nebeneinander vorliegen können. Zudem kann man mit ihr die an einem bestimmten Punkt im Phasendiagramm maximal möglichen Freiheitsgrade bestimmen. Für ein physikalisch homogenes thermodynamisches System reichen zwei Zustandsgrößen zur Bestimmung des Gleichgewichtszustands aus.

Für Fluide, also Gase und Flüssigkeiten, lautet sie:

$f\;=\;N\;-\;P\;+\;2$

• N - Anzahl der Komponenten im System (z. B. H₂O, CO₂)
• P - Anzahl der Phasen (verschiedene Aggregatzustände einer oder mehrerer Komponenten oder koexistierende flüssige Phasen (z. B. sind Wasser und Öl nicht mischbar und bilden zwei Phasen))
• f - Anzahl der Freiheitsgrade

Daraus folgt zum Beispiel für ein einkomponentiges System (N = 1), welches in zwei verschiedenen Aggregatzuständen (P = 2) vorliegt, dass es genau einen verbleibenden Freiheitsgrad gibt, das heißt eine Koexistenzlinie im Phasendiagramm. Existieren gleichzeitig drei Phasen (z. B. Wasser flüssig, gasförmig und fest), so verbleibt genau ein Punkt im Phasendiagramm, der Tripelpunkt, da kein Freiheitsgrad verbleibt.

Weiterhin folgt, dass es in einem einkomponentigen System an einer Stelle maximal drei koexistierende Phasen geben kann, da 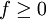$f \geq 0$; in einem zweikomponentigen vier Phasen, usw..

Da bei Feststoffen eine (geringe) Änderung des Druckes keine beziehungsweise nur sehr geringe Auswirkungen hat, lautet die Gibbssche Phasenregel in diesem Fall:

$f\;=\;N\;-\;P\;+\;1$

Diese Vereinfachung gilt jedoch nicht bei höheren Drücken, wie sie beispielsweise bereits in der Erdkruste vorliegen. Für die Druck- und Temperaturermittlung in der Geothermobarometrie ist dies für die korrekte Erfassung der jeweiligen Gleichgewichts-Paragenese von großer Bedeutung.

Die Herleitung der Gibbsschen Phasenregel erfolgt über die Gibbs-Duhem-Gleichung, die zeigt, dass in einem thermodynamischen System nicht alle intensiven Variablen unabhängig voneinander veränderlich sind.

Siehe auch: Kritischer Punkt, Tripelpunkt, Phasengrenzlinie, Eulerscher Polyedersatz