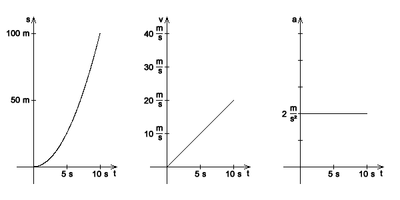
Gleichmäßig beschleunigte Bewegung

Beispiel einer gleichmäßig beschleunigten Bewegung mit Anfangsgeschwindigkeit v₀ = 0 und Anfangsweg s₀ = 0: Aufgetragen sind die Strecke s, Geschwindigkeit v und Beschleunigung a als Funktionen der Zeit t.

Eine gleichmäßig beschleunigte Bewegung ist eine Bewegung, bei der die Beschleunigung bezüglich Stärke und Richtung konstant ist. Die gleichmäßig beschleunigte Bewegung ist eine geradlinige Bewegung, wenn Beschleunigung und Geschwindigkeit kollinear sind. Ist dies nicht der Fall, entsteht eine Parabelbahn als Ortskurve. Wenn die Beschleunigung zu Null wird, erhält man die gleichförmige Bewegung.

Beispiele für eine gleichmäßig beschleunigte Bewegung sind der freie Fall oder der schräge Wurf ohne Berücksichtigung der Luftreibung.

Gesetze

Sofern die gleichmäßig beschleunigte Bewegung geradlinig ist, kann man für Berechnungen Zahlen (Skalare) statt Vektoren verwenden (Skalarform). Es genügt, die Orientierung des Geschwindigkeits- und des Beschleunigungsvektors durch das Vorzeichen auszudrücken. Eine Richtung (meist die Bewegungsrichtung) wird als positiv ausgezeichnet, die Gegenrichtung als negativ.

Verläuft die gleichmäßig beschleunigte Bewegung nicht geradlinig, so ist die allgemeinere Vektorform zu verwenden. Es gelten folgende Gesetze:

Gleichmäßig beschleunigte Bewegung
		Skalarform		Vektorform
notwendige Bedingung		a = const.		$\vec{a} = \text{const.}$
Geschwindigkeits-Zeit-Gesetz		$v(t) = \dot{s}(t) = a t + v_0$		$\vec{v}(t) = \dot{\vec{s}}(t) = \vec{a} t + \vec{v}_0$
Weg-Zeit-Gesetz		$s(t) = \frac{a}{2} t^2 + v_0 t + s_0$		$\vec{s}(t) = \frac{\vec{a}}{2} t^2 + \vec{v}_0 t + \vec{s}_0$
verwendete Formelzeichen
$a, \vec{a}$	Beschleunigung		$\left[ \frac{\text{m}}{\text{s}^2} \right]$	$\begin{align} \vec{a} &= \frac{\mathrm{d} \vec{v}(t)}{\mathrm{d} t} = \dot{\vec{v}}(t) \\ &= \frac{\mathrm{d}^2 \vec{s}(t)}{\mathrm{d} t^2} = \ddot{\vec{s}}(t) \end{align}$
$s(t), \vec{s}(t)$	Position zum Zeitpunkt t		$\left[ \text{m} \right]$	zurückgelegter Weg: $\vec{s}(t)-\vec{s}_0$
$s_0, \vec{s}_0$	Anfangsposition (Anfangsweg) zum Zeitpunkt t = 0		$\left[ \text{m} \right]$	$\vec{s}_0 = \vec{s}(t=0)$
t	Zeit		$\left[ \text{s} \right]$
$v(t), \vec{v}(t)$	Geschwindigkeit zum Zeitpunkt t		$\left[ \frac{\text{m}}{\text{s}} \right]$	$\vec{v}(t) = \frac{\mathrm{d} \vec{s}(t)}{\mathrm{d} t} = \dot{\vec{s}}(t)$
$v_0, \vec{v}_0$	Anfangsgeschwindigkeit zum Zeitpunkt t = 0		$\left[ \frac{\text{m}}{\text{s}} \right]$	$\vec{v}_0 = \vec{v}(t=0)$

Herleitung mit Hilfe der Integral- und Differentialrechnung

Es gilt

$\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} = \vec{a} \Rightarrow \mathrm{d}\vec{v}=\vec{a} \, \mathrm{d}t$

Durch unbestimmte Integration beider Gleichungsseiten über der Zeit erhält man bei konstanter Beschleunigung:

$\int \mathrm{d}\vec{v}=\vec{a} \int \mathrm{d}t$.

Nach der Ausführung der Integration erhält man für die Geschwindigkeit

$\vec{v}=\vec{a} t + \vec{v}_{0}$,

wobei $\vec{v}_{0}$ die Integrationskonstante ist, welche die Anfangsgeschwindigkeit beinhaltet.

Weiterhin ist bekannt, dass die Geschwindigkeit $\vec{v}$ die erste Ableitung der Position $\vec{s}$ nach der Zeit t ist:

$\frac{\mathrm{d}\vec{s}}{\mathrm{d}t}=\vec{v}$;

$\mathrm{d}\vec{s}=(\vec{a} t + \vec{v}_{0})\,{\mathrm{d}t}$;

sie gibt somit die Änderungsgeschwindigkeit der Position an. Durch anschließende unbestimmte Integration erhält man die Position:

$\vec{s}(t) = \frac{\vec{a}}{2} t^2 + \vec{v}_0 t + \vec{s}_0 \text{,}$

wobei $\vec{s}_0$ die Anfangsposition ist.

Durch diese Überlegungen haben wir nun Gleichungen für die Momentangeschwindigkeit $\vec{v}(t)$ zum Zeitpunkt t sowie die Momentanposition $\vec{s}(t)$ zum Zeitpunkt t erhalten:

$\begin{align} &\vec{v}(t) = \vec{a} t + \vec{v}_0 \\ &\vec{s}(t) = \frac{\vec{a}}{2} t^2 + \vec{v}_0 t + \vec{s}_0 \end{align}$

Weblinks

 Wikibooks: Formelsammlung_Physik/_Mechanik – Lern- und Lehrmaterialien