Wurfparabel

Unterschied zwischen einem schiefen Wurf ohne jegliche Reibung (schwarz), mit Stokes-Reibung (blau) sowie mit Newton-Reibung (grün)

Die Wurfparabel ist die Flugbahn, die ein Körper beim schiefen Wurf in einem homogenen Schwerefeld beschreibt, wenn man den Einfluss des Luftwiderstands vernachlässigt. Diese Vernachlässigung ist bei niedrigen Geschwindigkeiten und kompakten Körpern oder im Vakuum möglich. Der Scheitel der Parabel befindet sich dabei am höchsten Punkt der Flugbahn, die Parabel ist nach unten geöffnet.

Die ballistische Kurve ist die von der idealen Wurfparabel abweichende Kurve unter Einfluss des Luftwiderstandes. Die Wurfparabel ist die Idealisierung der ballistischen Flugbahn.

Wurfparabel ohne Luftwiderstand

Grund für die Parabelform ist die Tatsache, dass während des Fluges nur die Schwerkraft auf den Körper einwirkt. Zur Berechnung wird die Anfangsgeschwindigkeit in die zueinander senkrechten Komponenten x und y zerlegt, die unabhängig voneinander behandelt werden können. Die horizontale x-Komponente ist völlig unabhängig von der vertikalen y-Komponente, die nach oben gerichtet sei. Das hat folgende Konsequenzen (Startpunkt sei x = 0, y = 0):

• In horizontaler Richtung fliegt der Körper nach dem ersten Newtonschen Gesetz mit konstanter Geschwindigkeit v_x dahin, da in dieser Richtung keine Kraft auf ihn wirkt; bei konstanter Geschwindigkeit ändert sich die Entfernung linear mit der Zeit. Für diese Entfernung gilt die Formel

$\!\ x = v_\mathrm{x} t$

• In vertikaler Richtung bewirkt die Schwerkraft eine konstante Beschleunigung nach unten, nämlich die Schwerebeschleunigung g = 9,81 m/s². Die Geschwindigkeit v_y ist:

$v_y = v_\mathrm{0y} - g t\, .$

Der Ort y ergibt sich daraus durch Integration über die Zeit zu:

$y = v_\mathrm{0y} t - \frac{g}{2} t^2\, .$

Mathematische Beschreibung

Der Körper wird mit einer Geschwindigkeit v₀ unter dem Winkel β schräg nach oben geworfen. Dann gilt für die Geschwindigkeitskomponenten, aus denen die Abwurfgeschwindigkeit durch lineare Superposition zusammengesetzt ist (unter Vernachlässigung des Luftwiderstands):

• horizontal: horizontale Komponente der Anfangsgeschwindigkeit:

$x(t) = v_{0} t \cos \beta\,$ und

• vertikal: vertikale Komponente der Anfangsgeschwindigkeit plus Geschwindigkeitsänderung durch konstante Beschleunigung:

$y(t) = v_{0} t \sin \beta - \frac{g}{2} t^2\, .$

Die vektorielle Bahngleichung lautet dann:

$\vec{r}(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} v_0 t \cos\beta \\ v_0 t \sin \beta -\frac{g}{2} t^2 \end{pmatrix}$

Die explizite Bahngleichung im Ortsraum (auflösen von x(t) nach t und in y(t) einsetzen) lautet:

$y(x) = \left(\tan \beta \right)x - \frac{g}{2{v_0}^2 \cos^2\beta}x^2$

(Bedeutung der weiteren Variablen: t ist die Zeit, g ist die Schwerebeschleunigung)

Reichweite

Die Reichweite R wird üblicherweise dadurch definiert, dass die Wurfparabel die Ausgangshöhe wieder erreicht, d. h.: $\!\ y(R) = 0$. Damit kann man die Bewegungsgleichung nach R auflösen und erhält:

$R = \frac{{v_0}^2}{g}\sin(2 \beta)$.

Startwinkel für die maximale Reichweite

Da die Sinusfunktion bei $90^\circ$ ihren größten Wert $\sin 90^\circ = 1$ hat, erreicht man bei Anfangshöhe h₀ = 0 die größte Reichweite für $\beta_\mathrm{max} = 45^\circ$.

Reichweite bei von Null verschiedener Anfangshöhe

Für $h_0\ne 0$ und $\beta\ne 0$ gilt die allgemeine Formel der Wurfweite:

$R = \frac{{v_0}^2}{2g} \sin(2 \beta) \left[ 1+ \left( 1 + \frac{2gh_0}{{v_0}^2 \sin^2 \beta} \right) ^{1/2} \right]$

Die maximale Reichweite und der zugehörige Startwinkel kann aus der einhüllenden Wurfparabel auch ohne Verwendung von Ableitungen bestimmt werden. Für h₀ > 0 ist $\beta_\mathrm{max} < 45^\circ$, für h₀ < 0 folgt umgekehrt $\beta_\mathrm{max} > 45^\circ$.

Scheitelpunkt

Der Scheitelpunkt wird erreicht, wenn die vertikale Geschwindigkeitskomponente ihren Nulldurchgang hat, d. h., wenn sich eine zuerst nach oben gerichtete Bewegung in eine nach unten gerichtete Bewegung umkehrt. Wenn der Wurf nach oben gerichtet war, dann ist die Schwerebeschleunigung entgegengesetzt zur vertikalen Bewegungsrichtung des Körpers und wirkt dann nicht beschleunigend, sondern verzögernd, bis sie ihn auf Null abgebremst hat und anschließend nach unten weiter beschleunigt. Im Scheitelpunkt wurde also die gesamte kinetische Energie (in vertikaler Richtung) umgesetzt in potentielle Energie.

Den Scheitelpunkt kann man berechnen, da der Wurf eine Parabelform hat, und der Scheitelpunkt somit zwischen den Nullstellen 0 und R liegt. Der Scheitelpunkt hat also die x-Koordinate $\frac{1}{2} R$. Die y-Koordinate erhält man durch die Bewegungsgleichung.

Aufgelöst, hat der Scheitelpunkt folgende Koordinaten:

$x_\mathrm{S} = \frac{\sin (2\beta)}{2} \frac{v_0^2}{g} = \sin \beta \cos \beta \frac{v_0^2}{g}$

$y_\mathrm{S} = \frac{v_0^2 \sin^2 \beta}{2g}$

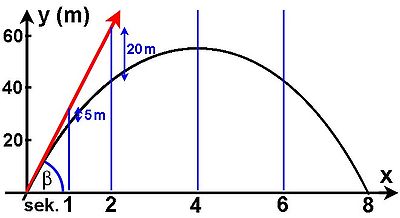
Erläuterung an einem Beispiel

Wurfparabel mit Höhen- und Zeitskala (Wurf mit ≈ 36 m/s unter 63°, Aufprall ohne Atmosphäre nach 8 s)

Wäre weder Gravitation noch Luftwiderstand vorhanden, würde der Körper in der anfänglichen Richtung und Geschwindigkeit (roter Pfeil) weiterfliegen (Trägheitsprinzip).

Das Erdschwerefeld lenkt den Körper jedoch nach unten ab – und zwar mit der Zeit t quadratisch zunehmend:

• Nach 1 s liegt die tatsächliche Flugbahn um knapp 5 m tiefer als die Tangente am Ausgangspunkt (Abwurfpunkt),
• nach 2 s um das 4-Fache (etwa 20 m),
• nach 3 s 45 m sowie
• nach 4 s 80 m und so weiter (Schwerebeschleunigung von 9,81 auf 10 m/s² gerundet).

Senkrechter Wurf

Der senkrechte Wurf ist ein wichtiger Spezialfall der Wurfparabel. Er lässt sich in zwei verschiedene Wurfrichtungen ausführen - nach oben (gegen die Schwerebeschleunigung) und nach unten (mit der Schwerebeschleunigung).

Der senkrechte Wurf nach oben entspricht einer ungestörten Überlagerung von geradlinig, gleichförmiger Bewegung nach oben und dem freien Fall nach unten. Wenn man dies in einer Grafik darstellt, so ergibt sich eine symmetrische Parabel, deren höchster Punkt dem Umkehrpunkt des Körpers entspricht. Dabei ergeben sich folgende Formeln:

$v = v_0 - g t\, ,$

$s = v_0 t - \frac{g}{2} t^2\, .$

• Die maximale Wurfhöhe $h_\mathrm{max}\,$,

wird berechnet, indem man die Geschwindigkeit v = 0 setzt, dann zunächst die

• Steigzeit $t_\mathrm{s} = \frac{v_0}{g}$

berechnet und schließlich mithilfe der unteren Gleichung s = h ermittelt.

Es ergibt sich:

$h_\mathrm{max} = \frac{{v_0}^2}{2\, g}\, .$

• Die Wurfdauer t_w berechnet man, indem man in der unteren Gleichung s = h = 0 setzt und dann die quadratische Gleichung für t löst. Einfacher kann die Wurfdauer, da die Fallzeit $\!\ t_\mathrm{f}$ gleich der Steigzeit $\!\ t_\mathrm{s}$ ist, jedoch durch Verdoppelung von Letzterer ermittelt werden.

Der senkrechte Wurf nach unten entspricht einer Überlagerung von geradliniger Bewegung nach unten und freiem Fall nach unten. Dabei ergeben sich folgende Formeln:

$v = v_0 + g t\, ,$

$h = h_0 - v_0 t - \frac{g}{2} t^2\, .$

Waagerechter Wurf

→ Hauptartikel: Waagerechter Wurf

Einen weiteren Spezialfall für den sich die Gleichungen vereinfachen bildet der waagerechte Wurf.

$\vec{r}(t) = \begin{pmatrix} v_0 t \\ -\frac{g}{2} t^2 \end{pmatrix}$

$\vec{v}(t) = \begin{pmatrix} v_0 \\ -g t \end{pmatrix}$

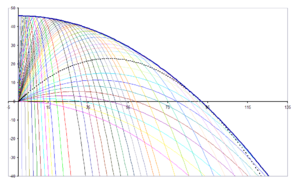
Einhüllende Wurfparabel

Hüllkurve der Wurfparabeln mit gemeinsamer Anfangsgeschwindigkeit – Die Wurfparabel mit 45°-Winkel ist gestrichelt hervorgehoben.

Wird bei gegebener Anfangsgeschwindigkeit v₀ (und Anfangshöhe h₀ = 0) der Startwinkel $\!\ \beta$ verändert, so erreichen die verschiedenen Wurfparabeln unterschiedliche Punkte in der (vertikalen) Wurfebene. Die Reichweite dieser Wurfparabeln wird durch die einhüllende Wurfparabel begrenzt.

Die Gleichung der Hüllkurve der Wurfparabeln $y(x) = x \tan \beta - \frac{g\,x^2}{2\,{v_0}^2 \cos^2\beta} + h_0$ lautet

$y_H (x) = \frac{{v_0}^2}{2\,g} - \frac{g\,x^2}{2\,{v_0}^2} + h_0$,

Sie entspricht demnach einem waagerechten Wurf ($\!\ \beta = 0$) aus der maximal erreichbaren Wurfhöhe des senkrechten Wurfs mit dessen Anfangsgeschwindigkeit v₀ und Anfangshöhe.

Wurfweite bei Würfen am Hang

Auch für Würfe an geneigten Ebenen kann man den Winkel für die maximale Reichweite bestimmen. Details finden sich in der englischsprachigen Wikipedia unter Rifleman’s rule.

Wurfparabel mit Luftwiderstand

Die Luftreibung und ein inhomogenes Schwerefeld nehmen Einfluss auf die Flugbahn. Dieser Einfluss ist Gegenstand der Ballistik.

• Luftwiderstand: Die Atmosphäre wirkt bremsend; je höher die Geschwindigkeit ist, desto stärker ist die Abweichung – denn der Luftwiderstand nimmt mit v² zu, die Bahnkrümmung (d. h.: die horizontale Streckung der Parabel durch höhere horizontale Geschwindigkeit) aber nur mit v ab. Die absteigende Kurve wird deutlicher gekürzt als die aufsteigende und verläuft daher steiler. Die maximale Wurfweite wird nicht mehr bei $\beta = 45^\circ$ erreicht. Außerdem muss beachtet werden, dass die Dichte der Luft in höheren Lagen geringer ist und damit ist auch der Luftwiderstand im Scheitelpunkt kleiner als am Boden.
• Inhomogenität des Schwerefelds
  • Kugelform der Erde: Die Lotlinien sind nicht parallel, sondern laufen im Erdzentrum zusammen. Daher würde auch im Vakuum keine Parabel resultieren, sondern eine Keplerellipse mit dem Brennpunkt im Geozentrum. Der Unterschied zur Parabel ist zwar bei üblichen Anwendungen nur im Millimeter-Bereich, wächst bei Raketen aber auf Kilometer an.
  • Lokale Variationen der Erdschwerebeschleunigung: Für Abweichungen der Schwerebeschleunigung auf der Erdoberfläche vom Schwerefeld einer idealen Kugel sorgen die Zentrifugalkraft der Erdrotation, die Erdabplattung (welche letztendlich eine Folge dieser Zentrifugalkraft ist), das Höhenprofil (Gebirge = große Masse, aber auch größere Entfernung vom Geozentrum) und die Massenverteilung im Untergrund (siehe Gravimetrie). Bspw. beträgt die Schwerebeschleunigung am Äquator $9{,}780\, \tfrac{\mathrm{m}}{\mathrm{s}^2}$, an den Polen jedoch $9{,}832\,\tfrac{\mathrm{m}}{\mathrm{s}^2}$. Findet der Wurf komplett in einem Bereich statt, in dem man die Schwerebeschleunigung als konstant annehmen kann, wird die Parabelform (bzw. Ellipsenform) zwar beibehalten, jedoch wird die Parabel durch eine geringere Schwerebeschleunigung weiter und durch eine höhere Schwerebeschleunigung enger. Ansonsten ergeben sich Abweichungen von der Parabelform.

Siehe auch

• Parabelflug
• Freier Fall
• Trajektorie (Physik)
• Ballistik
• Effektive Reichweite (Waffe)

Weblinks

• Java-Applet zur Veranschaulichung des schiefen Wurfs