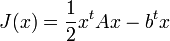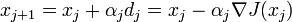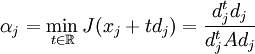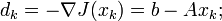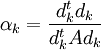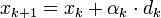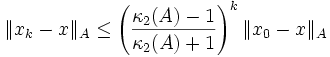Gradientenabstiegsverfahren

Das Verfahren des steilsten Abstiegs, auch Gradientenverfahren genannt, ist ein Verfahren, das in der Numerik eingesetzt wird, um allgemeine Optimierungsprobleme zu lösen. Dabei geht man (am Beispiel eines Minimierungsproblemes) von einem Näherungswert aus. Von diesem schreitet man in Richtung des negativen Gradienten (der die Richtung des steilsten Abstiegs von diesem Näherungswert angibt) fort, bis man keine numerische Verbesserung mehr erzielt.

Das Verfahren konvergiert oftmals sehr langsam, da es sich dem Optimum entweder mit einem starken Zick-Zack-Kurs nähert oder der Betrag des Gradienten in der Nähe des Optimums sehr klein ist, wodurch die Länge der Iterationsschritte dann ebenfalls sehr klein ist. Für die Lösung von symmetrisch positiv definiten linearen Gleichungssystemen bietet das Verfahren der konjugierten Gradienten hier eine immense Verbesserung. Der Gradientenabstieg ist dem Bergsteigeralgorithmus (hill climbing) verwandt.

Beschreibung des Verfahrens

Typischerweise wird ein Energiefunktional der Form

$J(x) = \frac{1}{2} x^tAx - b^tx$

minimiert. Dabei ist A eine symmetrisch positiv definite Matrix. Ausgehend von einem Anfangspunkt x₀ wird die Richtung des steilsten Abstiegs natürlich durch die Ableitung 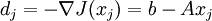$d_j = -\nabla J(x_j) = b - Ax_j$ bestimmt, wobei $\nabla$ den Nabla-Operator bezeichnet. Dann wird wie folgt iteriert

$x_{j+1} = x_j + \alpha_j d_j = x_j - \alpha_j \nabla J(x_j)$

α_j bezeichnet die Schrittweite des Verfahrens und kann durch

$\alpha_j = \min_{t \in \mathbb{R}} J(x_j + t d_j) = \frac{d^t_j d_j}{d^t_j A d_j}$

berechnet werden. Das Verfahren konvergiert dann für einen beliebigen Startwert gegen einen Wert x ^* , so dass J(x ^* ) minimal ist.

Algorithmus in Pseudocode

Eingabe: geeigneter Startvektor $\ x_0$

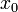
For k = 0 To n

$d_k = -\nabla J(x_k) = b - Ax_k;$

$\alpha_k = \frac{d^t_k d_k}{d_k^t A d_k}$

$x_{k+1} = x_k + \alpha_k \cdot d_k$

end

Ausgabe: Minimum des Energiefunktionals.

Konvergenzgeschwindigkeit

Das Gradientenverfahren liefert eine Folge 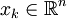$x_k \in \mathbb{R}^n$ mit

$\|x_k - x\|_A \leq \left( \frac{\kappa_2 (A) - 1}{\kappa_2 (A) + 1} \right)^k \|x_0 - x\|_A$

Dabei bezeichnet κ₂ die Kondition der Matrix A. Das Verfahren konvergiert allerdings oftmals sehr langsam, da es sich dem Optimum entweder mit einem starken Zick-Zack-Kurs nähert oder der Betrag des Gradienten in der Nähe des Optimums sehr klein ist, wodurch die Länge der Iterationsschritte dann ebenfalls sehr klein ist. Für die Lösung von linearen Gleichungssystemen bietet das CG-Verfahren hier eine immense Verbesserung.

Literatur

• Andreas Meister: Numerik linearer Gleichungssysteme. 2. Auflage. Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7.