Grashofzahl

Die Grashof Zahl Gr (nach: Franz Grashof 1826-1893) ist eine dimensionslose Kennzahl in der Strömungslehre. Sie gibt das Verhältnis des Auftriebs eines Fluides zur wirkenden Viskositätskraft an.

Sie ist definiert als:

$Gr = \frac{g \cdot \beta \,({T}_s-{T}_{\infty}) \,{L}^3}{\nu^2}$

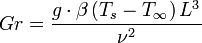
• g Fallbeschleunigung (bspw. in SI-Einheiten: ≈9,81 m/s²)
• β Wärmeausdehnungskoeffizient (bspw. in SI-Einheiten: 1/K)
• T_s Temperatur (bspw. in SI-Einheiten: K)
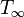• $T_{\infty}$ Ruhe-Temperatur (bspw. in SI-Einheiten: K)
• L Charakteristische Länge (bspw. in SI-Einheiten: m)
• ν kinematische Viskosität (bspw. in SI-Einheiten: m²/s)

Bei der Herleitung beim Dimensionslosmachen den Navier-Stokes-Gleichungen ergibt sich die zu oben äquivalente Form

$Gr = \frac{|\rho-\rho_0|}{\rho_0} \frac{g \cdot L^3}{\nu^2}$

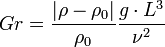
• ρ Dichte (bspw. in SI-Einheiten: kg/m³)
• ρ₀ Dichte im ungestörten Fluid

Man kann die Grashof-Zahl auch in eine äquivalente Reynolds-Zahl umrechnen, um anschließend die Formeln der freien Konvektion auf die erzwungene anwenden zu können. Die Umrechnung erfolgt gemäß:

$Re_{\ddot{a}qu} = \sqrt{0{,}4 \cdot Gr}$

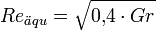
Weblinks

• Weitere Informationen (engl.)