Gruppierter Brierscore

Während ordinale Insolvenzprognosen lediglich eine Reihung von Unternehmen entsprechend den erwarteten Ausfallwahrscheinlichkeiten vornehmen, ordnen kardinale Insolvenzprognosen jedem Unternehmen explizit eine Ausfallwahrscheinlichkeit zu.^[1]

Fundamentale Kriterien für die Bewertung von Insolvenzprognosen

Da sich Ausfallwahrscheinlichkeiten auch als Reihungskriterium interpretieren lassen, können kardinale Insolvenzprognosen hinsichtlich aller Gütekriterien bewertet werden, die auch für ordinale Insolvenzprognosen anwendbar sind: ^[2],^[3]

• Auflösung (resolution) misst, wie stark differenziert die realisierten Ausfallquoten bezogen auf die unterschiedlichen Ratingklassen sind. Minimale Auflösung ist dann gegeben, wenn für alle Ratingklassen die gleichen realisierten Ausfallquoten zu verzeichnen sind. Maximale Auflösung ist dann gegeben, wenn in den einzelnen Ratingklassen 0%- oder 100%-Ausfallquoten auftreten,

• Trennfähigkeit (discrimination) misst, wie stark sich die Prognosen bei tatsächlich ausgefallenen/ tatsächlich nicht ausgefallenen Unternehmen unterscheiden.

Zusätzlich können aber auch Kriterien geprüft werden, bei denen die ex-ante Angabe von Ausfallwahrscheinlichkeiten zwingend erforderlich ist:

• Kalibrierung misst für Gruppen von Prognosen (Ratingklassen), wie gut die prognostizierten Ausfallwahrscheinlichkeiten mit den realisierten Ausfallquoten übereinstimmen,

• systematische Verzerrung (unconditional bias): gibt an, wie stark sich die durchschnittliche prognostizierte Ausfallwahrscheinlichkeit von der tatsächlichen Ausfallquote unterscheidet,

• Feinheit (refinement) misst, wie stark differenziert die Ausfallprognosen sind. Minimale Feinheit ist dann gegeben, wenn stets eine identische Ausfallwahrscheinlichkeit prognostiziert wird; maximale Feinheit ist dann gegeben, wenn nur 0%- oder 100%-Prognosen abgegeben werden.

Kennzahlen die simultan von allen oder einigen dieser Eigenschaften kardinaler Insolvenzprognosen determiniert werden, werden im folgenden als Maße für die Präzision (accuracy) eines Verfahrens bezeichnet. Kennzahlen, welche die Präzision eines Prognoseverfahrens ins Verhältnis zur Präzision eines bestimmten Referenzverfahrens setzen, werden als Maße der Relativen Präzision (auch skill scores oder relative accuracy) bezeichnet.^[4]

Kennzahlen zur Messung der Kalibrierung von Insolvenzprognosen

Kennzahlen die nur einzelne der oben aufgeführten Aspekte kardinaler Insolvenzprognosen messen, insbesondere den Aspekt der Kalibrierung, sind beispielsweise der Gruppierte Brier-Score oder der Rommelfanger-Index.

Gruppierter Brier-Score

Der Gruppierte Brier-Score ist wie folgt definiert^[5]

Formel 1: $\mathrm{Brier}_\mathrm{gruppiert} = \frac{1}{g} \sum_{i=1}^g (PD_{i,\mathrm{prog}} - PD_{i, \mathrm{tat}})^2$

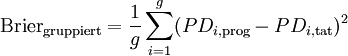
mit PD_{i,prog / tat} für Ratingklasse i prognostizierte / realisierte Ausfallrate,

g: Anzahl der Ratingklassen

Anmerkung: Eine naheliegende Alternative zur Gleichgewichtung der ratingklassenspezifischen quadrierten Differenzen der prognostizierten und realisierten Ausfallquoten bei der Ermittlung des Scores besteht in der Berücksichtigung der relativen Belegungsstärken der einzelnen Ratingklassen:

Formel 1b: $\mathrm{Brier}_\mathrm{gruppiert}' = \sum_{i=1}^g a_i(PD_{i,\mathrm{prog}} - PD_{i,\mathrm{tat}})^2$

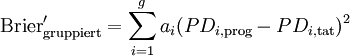
mit a_i: Anteil der Unternehmen in Ratingklasse i an allen Unternehmen

Trotz des ähnlichen Aufbaus unterscheiden sich der gruppierte Brier-Score und der Brier-Score, der im folgenden vorgestellt wird, grundlegend. Im Gegensatz zum Brier-Score (siehe unten) wird der gruppierte Brier-Score nur von der Güte der Kalibrierung eines Ratingverfahrens beeinflusst - nicht jedoch von allen anderen Kriterien kardinaler Schätzgütemaße.

Rommelfanger-Index

Der Rommelfanger-Index ist wie folgt definiert^[6]:

Formel 2: $F= \sum_{i=1}^g \Delta_i \frac{a_i+ \hat{a}_i}{2}f_i$

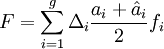
mit Δ_i = max(0;PD_i,tat − PD_i,prog) für i=1 … g-1, bzw. Δ_i = max(0;PD_i,prog − PD_i,tat) für i=g,

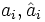$a_i, \hat{a}_i$: relatives Volumen aller Kredite in der Validierungs-/ Lernstichprobe,

f_i: „geeignetes Gewicht“ ^[7]

Anmerkung: Es wird keine Aussage darüber getroffen, wie die „geeigneten Gewichte“ beschaffen sein müssen. Weitere Kritikpunkte an dieser Kenngröße, neben der ausschließlichen Fokussierung auf den Aspekt der Kalibrierung, sind die Abhängigkeit von irrelevanten Größen (Struktur der Lernstichprobe) und die Setzung von Anreizen zu systematischen Fehlprognose: da in den Klassen 1 … g-1 nur zu hohe und in der Klasse g nur zu niedrige Ausfallwahrscheinlichkeiten „bestraft“ werden, besteht ein Anreiz, alle Prognosen systematisch zu hoch (Ratingklasse 1 … g-1) bzw. zu niedrig (Ratingklasse g) anzusetzen.

Weitere Kennzahlen zur Messung der Kalibrierung von Insolvenzprognosen

Weitere Kenngrößen, die ausschließlich die Korrektheit der Kalibrierung einzelner oder aller Ratingklassen überprüfen, sind Teststatistiken des Binomialtests, des χ²-Tests oder des Normalverteilungstests.^[8]

Universelle Schätzgütemaße für kardinale Insolvenzprognosen

Grundlegender Aufbau universeller Schätzgütemaße für kardinale Insolvenzprognosen

Die beiden im folgenden vorgestellten Präzisionsmaße kardinaler Insolvenzprognosen basieren auf einem einheitlichen Grundprinzip: sie vergleichen die individuellen prognostizierten Ausfallwahrscheinlichkeiten PD_i,prog mit den realisierten Ausfallergebnissen Θ_i (mit Θ_i = 1 / Θ_i = 0 falls Schuldner i ausgefallen/ nicht ausgefallen ist) und belegen die dabei auftretenden Differenzen mit unterschiedlichen „Strafen“. Auf diese Weise werden sie von allen der oben aufgeführten fundamentalen Kriterien für die Bewertung von Ausfallprognosen beeinflusst - und nicht nur von einzelnen dieser Maße.

Im Gegensatz zu kategorialen Insolvenzprognosenverfahren, die nur die Extremprognosen „Ausfall“ vs. „Nichtausfall“ erlauben, ist bei stochastischen Ausfallprognosen (kardinalen Ausfallprognosen) zunächst fraglich, warum Abweichungen der individuellen Prognosen (Ausfallwahrscheinlichkeiten) und Ausfallrealisierung als Fehler „bestraft“ werden sollten. Schließlich können die Prognosen beliebige Werte zwischen 0% und 100% annehmen, während die Ausfallrealisierungen nur die Extremenwerte 1 („Ausfall“) oder 0 („Nichtausfall“) annehmen können. Selbst wenn die prognostizierten Ausfallwahrscheinlichkeiten „richtig“ sind, d.h. korrekt kalibriert sind, wenn also beispielsweise 5% aller Unternehmen ausfallen, bei denen das Verfahren eine Ausfallwahrscheinlichkeit von 5% vorhergesagt hat und 10% aller Unternehmen ausfallen, bei denen das Verfahren eine Ausfallwahrscheinlichkeit von 10% vorhergesagt hat, usw., werden die Verfahren „bestraft“, d.h. erhalten nicht die bestmögliche Ausprägung. „Bestraft“ wird in diesen Fällen jedoch die nicht perfekte Trennschärfe der Verfahren: ein Verfahren, das bei allen deutschen Unternehmen im Jahr 2003 eine Insolvenzwahrscheinlichkeit von 1,35% vorausgesagt hätte, wäre zwar perfekt kalibriert gewesen, hätte aber eine hohe „Strafe“ für seine nicht-trennscharfen Prognosen erhalten. Ein Verfahren hingegen, das bei 1,35% dieser Unternehmen eine Insolvenzwahrscheinlichkeit von 100% und bei den restlichen 98,65% eine Ausfallwahrscheinlichkeit von 0% vorhergesagt und mit diesen Prognosen auch immer recht gehabt hätte, hätte die bestmögliche Bewertung erhalten.^[9]

Zwei übliche Präzisionsmaße für die Bewertung kardinaler Insolvenzprognosen, die sich nur hinsichtlich der konkreten Ausprägung ihrer „Straffunktionen“ unterscheiden, sind die bedingte Informationsentropie und der Brier-Score.

Bedingte Informationsentropie

Die bedingte Informationsentropie (CIE, conditional information entropy) basiert auf einer logarithmischen „Straffunktion“. Die Entropie stellt ein aus der Thermodynamik entlehntes Konzept dar, welches das Ausmaß an Unordnung eines Systems messen soll. Im Kontext von Insolvenzprognosen soll die bedingte Informationsentropie das Ausmaß an Unsicherheit quantifizieren, das mit der mit einem Ratingmodell ermittelten Ausfallwahrscheinlichkeitenverteilung eines Portfolios von Unternehmen verbunden ist. ^[10]

Formel 3: 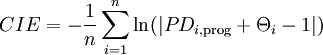$CIE = -\frac{1}{n} \sum_{i=1}^n \ln(|PD_{i,\mathrm{prog}} + \Theta_i-1|)$^[11]

mit n: Anzahl der Schuldner

Anmerkung: nicht definiert ist CIE nur für die Fälle, in denen ein Ausfall eintritt, obwohl er mit Sicherheit ausgeschlossen wurde (Θ_i = 1 und PD_i,prog = 0) oder in denen kein Ausfall eintritt, obwohl er mit Sicherheit prognostiziert wurde (Θ_i = 0 und PD_i,prog = 1).

Formel 4: $E(CIE)=- \frac {1}{n} \sum_{i=1}^n PD_{i,\mathrm{tat}} \cdot \ln PD_{i,\mathrm{prog}} + (1-PD_{i,\mathrm{tat}}) \cdot \ln(1-PD_{i,\mathrm{prog}})$

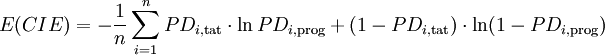
im Fall von g diskreten Ratingklassen ergibt sich:

Formel 4b: $E(CIE)=- \sum_{i=1}^g a_i \cdot \Big( PD_{i,\mathrm{tat}} \cdot \ln PD_{i,\mathrm{prog}} + (1-PD_{i,\mathrm{tat}}) \cdot \ln(1-PD_{i,\mathrm{prog}}) \Big)$

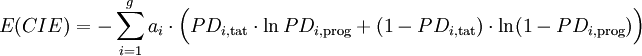
mit a_i Anteil der Unternehmen in Ratingklasse i an allen Unternehmen

Formel 5: $\mathrm{Skill}_{CIE}\equiv CIER = \frac {CIE_{PD}-CIE} {CIE_{PD}}$

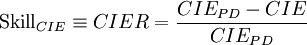
Formel 6: $CIE_{PD}=- \Big( PD \cdot \ln PD + (1-PD) \cdot \ln(1-PD) \Big)$

mit CIER: conditional information ratio^[12]

und CIE_PD: CIE-Wert einer „naiven“ Referenzprognose, die stets die Wahrscheinlichkeit PD prognostiziert ^[13],^[14]

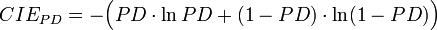
Anmerkung: Der Term CIE_PD − CIE wird auch als Kullback-Leibler-Distanz^[15] oder Wealth-Growth-Rate-Pickup^[16] bezeichnet. Der Term CIER entspricht der für die Messung der Anpassungsgüte von logistischen Regressionsschätzungen üblicherweise verwendeten Kenngröße McFadden’s-r².^[17]

Brier-Score

Im Gegensatz zur bedingten Informationsentropie (CIE) basiert der Brier-Score auf einer quadratischen Funktion, mit der Abweichungen der prognostizierten Ausfallwahrscheinlichkeiten von den Ausfallrealisationen „bestraft“ werden. Er ist wie folgt definiert:

Formel 7: 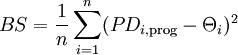$BS = \frac{1}{n} \sum_{i=1}^n (PD_{i,\mathrm{prog}}- \Theta_i)^2$ ^[18]

Formel 8: $E(BS) = \frac{1}{n} \sum_{i=1}^n PD_{i,\mathrm{tat}} \cdot (1-PD_{i,\mathrm{prog}})^2 + (1-PD_{i,\mathrm{tat}}) \cdot PD_{i,\mathrm{prog}}^2$

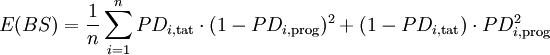
im Fall von g diskreten Ratingklassen entspricht dies:

Formel 8b: $E(BS)= \sum_{i=1}^g a_i \cdot \Big( PD_{i,\mathrm{tat}} \cdot (1-PD_{i,prog})^2 + (1-PD_{i,\mathrm{tat}}) \cdot PD_{i,\mathrm{prog}}^2 \Big)$

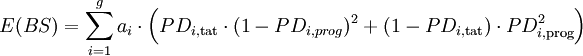
Formel 9: 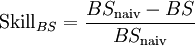$\mathrm{Skill}_{BS}= \frac{BS_\mathrm{naiv}-BS}{BS_\mathrm{naiv}}$ mit

Formel 10: $BS_\mathrm{naiv} = PD \cdot (1-PD)^2 + (1-PD) \cdot PD^2 = PD \cdot (1-PD)$

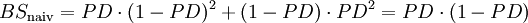
Anmerkung: In der im Kontext von Regressionsanalysen verwendeten Notation entspricht BS_naiv der mit n dividierten Summe der absoluten Variation der zu erklärenden Variable (TSS). Somit gilt Skill_BS = (TSS – RSS)/ TSS (mit RSS: Fehlerquadratsumme). Somit gilt Skill_BS = r², mit r²: Bestimmtheitsmaß ("Regression-r²") und r² = ESS/TSS und ESS=TSS-RSS.^[19]

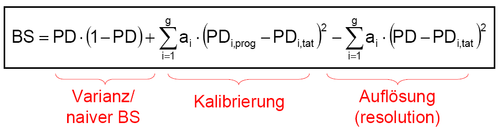
Die „Straffunktionen“ der bedingten Informationsentropie und des Brier-Scores sind als willkürlich in dem Sinne anzusehen, als dass sie nicht Bezug auf die letztendlich interessierenden (und möglicherweise differierenden) Nutzengrößen der Anwender des Prognoseverfahrens nehmen. Die Kenngrößen zeigen jedoch ein „plausibles“ Verhalten, so dass eine Korrelation mit den Nutzengrößen der potentiellen Anwender der Prognosen zumindest vermutet werden kann: Beide Scores „belohnen“ richtig kalibrierte ^[20] und trennfähige ^[21] Prognosen - und durch Umformungen der resultierenden Scorewerte lassen sich auch Bezüge zu den anderen Gütekriterien für kardinale Insolvenzprognosen, wie Auflösung, Feinheit, systematische Verzerrung, herstellen.^[22]

Umweltabhängigkeit kardinaler Schätzgütemaße

Aus der in obiger Abbildung dargestellten Dekomposition des Brier-Scores wird jedoch eine problematische Eigenschaft des Brier-Scores (und anderer kardinaler Gütemaße) ersichtlich: die Abhängigkeit von der durchschnittlichen Ausfallrate der Grundgesamtheit. Je größer die Varianz der Umgebung (PD·(1-PD)) ist, desto größer (=schlechter) ist der Brier-Score, den ein Verfahren in der jeweiligen Umgebung erzielt.^[23]. Um diese unerwünschte Umweltabhängigkeit kardinaler Gütemaße zu vermeiden, wird die Verwendung von Skillmaßen vorgeschlagen, die den ermittelten Gütewert in Relation zur Güte von naiven Prognosen in der gleichen Umgebung betrachten.^[24]

Unerwünscht ist diese Abhängigkeit, weil sie den Performancevergleich unterschiedlicher Verfahren beeinträchtigt, wenn die Leistungsfähigkeit der Verfahren auf Grundgesamtheiten mit unterschiedlichen durchschnittlichen Ausfallhäufigkeiten gemessen werden. Empirisch und (modell-)theoretisch lässt sich jedoch zeigen, daß auch Skill-Scores umweltabhängig sind – während der Brier-Score (für PD_i<50%) mit zunehmenden Ausfallwahrscheinlichkeiten immer „schlechter“ wird, werden die zugehörigen Skillscores aber paradoxerweise immer „besser“. ^[25] Schätzgütemaße für ordinale Insolvenzprognosen weisen diesen Nachteil nicht auf.^[26]

Vereinzelt werden obige Gütemaße auch unter der Fiktion einer richtigen Kalibrierung verwendet, d.h. ex-post wird PD_i,prog = PD_i,tat für alle i gesetzt.^[27] Die Formeln 4b und 8b vereinfachen sich dann zu:

Formel 4c: $CIE_\mathrm{kalibriert}=- \sum_{i=1}^g a_i \cdot \Big( PD_i \cdot \ln PD_i + (1-PD_i) \cdot \ln(1-PD_i) \Big)$

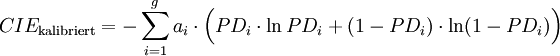
Formel 8c: $BS_\mathrm{kalibriert}= \sum_{i=1}^g a_i \cdot \Big( PD_i \cdot (1-PD_i)^2 + (1-PD_i) \cdot PD^2 \Big)$

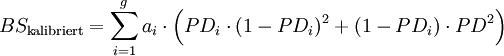
Formel 8d:$BS_\mathrm{kalibriert}= \sum_{i=1}^g a_i \cdot PD_i \cdot (1-PD_i)$

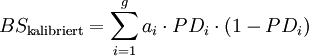
Die so erhaltenen Gütemaße sind dann unempfindlich gegenüber möglichen Fehlkalibrierungen (oder gar fehlenden Kalibrierungen, wie im Fall ordinaler Insolvenzprognosen) - der mittlere Term („Kalibrierung“) in obiger Abbildung entfällt - und sie messen somit lediglich die Varianz der Umwelt und die Auflösung der Prognosen. Für portfolioübergreifende Vergleich sind sie aber aufgrund der Abhängigkeit von der durchschnittlichen Ausfallrate ungeeignet. Beim Vergleich verschiedener Prognoseverfahren auf Basis identischer Portfolien sind sie zwar nicht informativer als die üblichen Schätzgütemaße für ordinale Insolvenzprognosen wie Area under the ROC curve und Accuracy Ratio, sie können aber als zusätzliches Kriterium herangezogen werden, speziell im Fall von einander schneidenden ROC-Kurven. Deuten beim direkten Vergleich zweier Prognoseverfahren alle Indikatoren auf die Überlegenheit des gleichen Verfahrens, so wird der Entscheidungsträger – wenn er sich für dieses Verfahren entscheidet, in seiner Sicherheit bestärkt, das richtige Verfahren gewählt zu haben. Geben die verschiedenen Indikatoren widersprüchliche Signale, ist anzunehmen, dass der Entscheidungsträger zumindest keinen „großen Fehler“ macht, wenn er sich für ein beliebiges der beiden Verfahren entscheidet. Alternativ kann er dann auch sekundäre Entscheidungskriterien heranziehen wie die Kosten der Prognoseerstellung oder die Transparenz und Nachvollziehbarkeit der Prognoseverfahren.

Quellen

1. ↑ Dieser Artikel basiert auf Bemmann (2005).
2. ↑ Siehe Murphy, Winkler (1992, S. 440) für die formalen Definitionen der im folgenden vorgestellten Gütekriterien resolution, discrimination, calibration, refinement, unconditional bias, accuracy und skill.
3. ↑ Auch die unter Schätzgütemaße für ordinale Insolvenzprognosen behandelten Kenngrößen Accuracy Ratio und Area under the ROC curve werden von der Auflösung und Trennfähigkeit der Prognosen beeinflusst.
4. ↑ siehe Murphy, Winkler (1992, S. 440)
5. ↑ Siehe beispielsweise Frerichs, Wahrenburg (2003, S. 16, eigene Notation). In einer Simulationsstudie finden die Autoren, dass der gruppierte Brier-Score nicht als Validierungskenngröße für Ratingsysteme geeignet ist, da er nicht in der Lage ist, „unterlegene“ Ratingsysteme zuverlässig zu identifizieren.
6. ↑ DVFA (2004, S. 600, eigene Notation)
7. ↑ siehe DVFA (2004, S. 599)
8. ↑ siehe Basler Ausschuss (2005a, S. 47ff.)
9. ↑ siehe auch Krämer (2003, S. 396f.)
10. ↑ Siehe Sobehart, Keenan, Stein (2000, S. 14). Siehe Shannon (1948, S. 11f.) für eine axiomatische Rechtfertigung für die Verwendung logarithmischer „Straffunktionen“ – allerdings ist das letzte dieser Axiome im Fall von Unternehmensinsolvenzen mit nur zwei möglichen Ausprägungen „Ausfall“ vs. „Nicht-Ausfall“ nicht sinnvoll anwendbar. Siehe ferner Matheson, Winkler (1976), Keenan, Sobehart (1999, S.9), und BASLER Ausschuss (2005a, S.44) für Formel F 27 (eigene Notation).
11. ↑ siehe Krämer, Güttler (2003, S. 12)
12. ↑ siehe Keenan, Sobehart (1999, S. 10)
13. ↑ Sobehart, Keenan, Stein (2000, S. 14): “The CIER compares the amount of ‘uncertainty’ regarding default in the case where we have no model (a state of more uncertainty about the possible outcomes) to the amount of ‘uncertainty’ left over after we have introduced a model (presumably, a state of less ignorance)",
14. ↑ Angesichts der im Zeitverlauf sehr volatilen Ausfallraten bei Unternehmen, ist die Prognose der künftigen PD keineswegs trivial. Siehe hierzu beispielsweise Keenan (1999) oder S&P (2004b, S.3).
15. ↑ siehe Basler Ausschuss (2005, S. 30)
16. ↑ siehe Cangemi, Servigny, Friedman (2003, S. 40)
17. ↑ siehe Scheule (2003, S. 51)
18. ↑ Für die Definition des Brier-Scores siehe Brier (1950, S. 1), Murphy, Winkler (1992, S. 439, Formel 7), Krämer, Güttler (2003, S. 11), Frerichs, Wahrenburg (2003, S.14), OeNB (2004a, S. 123ff.), Grunert, Norden, Weber (2005, S.517)
19. ↑ siehe Gujarati (1999, S. 170ff.)
20. ↑ Diese Aussage ist nicht trivial. Wird als Straffunktion beispielsweise | PD_i,prog − Θ_i | verwendet, so führt PD_i,prog = 0 für E(PD_i,tat) < 0,5 und PD_i,prog = 1 für E(PD_i,tat) > 0,5 zu geringeren erwarteten Strafen als PD_i,prog = E(PD_i,tat), siehe Bemmann (2005, Anhang II). Siehe ebenda für den Beweis der Anreizkompatibilität des Brier-Scores und der bedingten Informationsentropie. Bereits Brier (1950, S.2) führt die Anreizkompatibilität als einen Vorteil des Brier-Scores an.
21. ↑ Beide Schätzgütemaße erreichen ihre günstigsten Ausprägungen, wenn ein Verfahren stets Ausfallwahrscheinlichkeiten von 0% oder 100% prognostiziert und die Prognosen auch eintreffen.
22. ↑ siehe Murphy, Winkler (1992)
23. ↑ siehe Bemmann (2005, Anhang III)
24. ↑ siehe Krämer (2003, S. 406) oder Winkler (1994, S. 1397): “The development of so called 'skill-scores' has been motivated by the desire to produce average scores that reflect the relative ability of forecaster rather than some combination of the forecaster’s ability to and the situation’s difficulty. These skill scores attempt to neutralize the contribution of the situation by comparing a forecaster’s average score to the average score that an unsophisticated forecasting scheme would have obtained for the same set of forecasting situations.”
25. ↑ siehe Winkler (1994, S. 1401f.) und Bemmann (2005, Anhang III)
26. ↑ siehe Bemmann (2003, Anhang)
27. ↑ siehe Krämer, Güttler (2003, S. 12)

Literatur

• Basler Ausschuss: siehe Basler Ausschuss für Bankenaufsicht

• Basler Ausschuss für Bankenaufsicht (Hrsg.) (2005a): “Studies on the Validation of Internal Rating Systems”, Working Paper No. 14, http://www.bis.org/publ/bcbs_wp14.pdf (24. Oktober 2005), überarbeitete Version, 05/2005

• Bemmann, M. (2005): "Verbesserung der Vergleichbarkeit von Schätzgüteergebnissen von Insolvenzprognosestudien",in Dresden Discussion Paper Series in Economics 08/ 2005, http://ideas.repec.org/p/wpa/wuwpfi/0507007.html (8. November 2006) und http://papers.ssrn.com/sol3/papers.cfm?abstract_id=738648 (27. November 2006), 2005

• Brier, G. W. (1950): “Verification of forecasts expressed in terms of probability”, Monthly Weather Review 78, S. 1 – 3, 1950

• Cangemi, B., Servigny, A. DE, Friedman, C. (2003): “Standard & Poor's Credit Risk Tracker for Private Firms, Technical Document”, S&P Working Paper, http://www.standardandpoors.co.jp/spf/pdf/rev_CRTTechDocument20031126.pdf (6. November 2006), 2003

• Deutsche Vereinigung für Finanzanalyse, Kommission Rating Standards, Arbeitskreis 2 „Validierung“ (DVFA, Hrsg.) (2004): „DVFA – Validierungsstandards“, in Finanz Betrieb, S. 596-601, 09/2004

• DVFA: siehe Deutsche Vereinigung für Finanzanalyse

• Frerichs, H., Wahrenburg, M. (2003): ”Evaluating internal credit rating systems depending on bank size”, Working Paper Series: Finance and Accounting, Johann Wolfgang Goethe-Universität Frankfurt Am Main, No. 115, http://ideas.repec.org/p/fra/franaf/115.html (14. November 2006), 09/2003

• Grunert, J., Norden, L., Weber, M. (2005): “The role of non-financial factors in internal credit ratings”, in Journal of Banking and Finance, Bd. 29, S. 509-531, 2005

• Gujarati, D. (1999): “Essentials of Econometrics”, Irwin/McGraw-Hill, 2. Auflage, 1999

• Keenan, S. C. (1999): “Predicting Default Rates: A Forecasting Model for Moody's Issuer-Based Default Rates”, Moody’s Investors Service, Special Comment, Report # 47729, http://www.moodyskmv.com/research/files/wp/47729.pdf (6. November 2006), 08/1999,

• Keenan, S. C., Sobehart, J.R. (1999): “Performance Measures for Credit Risk Models”, Moody’s Investors Service, Research Report # 1-10-10-99, http://www.riskmania.com/pdsdata/PerformanceMeasuresforCreditRiskModels.pdf (6. November 2006), 1999

• Krämer, W. (2003): „Die Bewertung und der Vergleich von Kreditausfall-Prognosen“, in Kredit und Kapital, Bd. 36 (3), S. 395-410, 2003

• Krämer, W., Güttler, A. (2003): “Comparing the accuracy of default predictions in the rating industry: The case of Moody’s vs. S&P”, Technical Report-Reihe des SFB 475 Nr. 23 (Universität Dortmund), http://www.wiwi.uni-frankfurt.de/schwerpunkte/finance/wp/332.pdf (6. November 2006), 2003

• Matheson, J. E., Winkler, R. L. (1976): „Scoring rules for continuous probability distributions“, in Management Sciences, Bd. 22, No. 10, 1976

• Murphy, A. H., Winkler, R. L. (1992): “Diagnostic verification of probability forecasts”, in International Journal of Forecasting, Bd. 7, S. 435-455, 1992

• OENB: siehe Österreichische Nationalbank

• Österreichische Nationalbank (Hrsg.) (2004a): „Ratingmodelle und -validierung”, Leitfadenreihe zum Kreditrisiko, http://www.nationalbank.at/de/img/leitfadenreihe_ratingmodelle_tcm14-11172.pdf (18. Oktober 2006), Wien, 2004

• Scheule, H. (2003): „Prognose von Kreditausfallrisiken“, zugelassene Dissertation Universität Regensburg, 2003, Uhlenbruch Verlag, Bad Soden/Ts., 2003

• Shannon, C.E. (1948): “A Mathematical Theory of Communication”, in Bell System Technical Journal, Bd. 27, 1948, S. 379–423, 623–656, reprinted in Mobile Computing and Communications Review, Bd. 5 (I), S. 3-55, 2001

• Sobehart, J. R., Keenan, S.C., Stein, R.M. (2000): „Benchmarking Quantitative Default Risk Models: A Validation Methodology”, Moody’s Investors Service, Rating Methodology, Report # 53621, http://www.moodysqra.com/us/research/crm/53621.pdf (6. November 2006), 03/2000

• S&P: siehe Standard and Poor's

• Standard and Poor's (Hrsg.) (2004b): „S&P Quarterly Default Update & Rating Transitions“, The McGraw Hills Companies, 10/2004

• Winkler, R. L. (1994): „Evaluating Probabilities: Asymmetric Scoring Rules“, in Management Science, Bd. 40, No. 11, S. 1395-1405, 1994