Hase-Igel-Algorithmus

Der Hase-Igel-Algorithmus ist ein Verfahren, mit dem in einer einfach verketteten Liste Schleifen mit der Zeitkomplexität O(n) und einer Platzkomplexität von O(1) gefunden werden können. Mathematisch betrachtet dient der Algorithmus zum Auffinden von Zyklen in Folgen. Er ist auch unter dem Namen Floyds Algorithmus zum Auffinden von Schleifen (englisch Floyd's cycle-finding algorithm) bekannt und darf nicht mit Floyds Algorithmus aus der Graphentheorie verwechselt werden.

Bedeutung in der Mathematik

Neben der trivial ersichtlichen Verwendung zum Auffinden von Schleifen in zur Ablage von Daten genutzten Listen ist der Hase-Igel-Algorithmus die Grundlage der Pollard-Rho-Methode zur Bestimmung der Periodenlänge einer Zahlenfolge einschließlich der darauf zurückführbaren Primfaktorzerlegung.

Der Algorithmus wird auch im Themenfeld der pseudozufälligen Folgen eingesetzt.

Prinzip

Der Algorithmus besteht aus dem gleichzeitigen Durchlauf der Liste mit unterschiedlichen Schrittweiten. Dabei werden zwei Zeiger auf Listenelemente benutzt, von denen der eine (Igel) bei jeder Iteration auf das nächste Element verschoben wird, während der andere (Hase) bei derselben Iteration auf das übernächste Element verschoben wird. Wenn die beiden Zeiger sich begegnen, also dasselbe Element referenzieren, hat die Liste eine Schleife. Wenn einer der beiden Zeiger das Ende der Liste erreicht, hat sie keine Schleife.

Begründung

Hase-Igel-Algorithmus

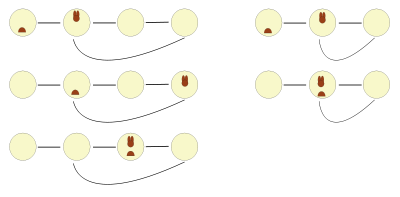
Am besten kann die Vorgehensweise visualisiert werden, indem in einem gezeichneten Diagramm der Weg der beiden Zeiger verfolgt wird. Es ist leicht ersichtlich, dass sowohl bei einer Schleife mit ungerader Anzahl von Elementen als auch bei einer Schleife mit gerader Anzahl der Hase in höchstens einem Durchlauf des Igels auf diesen trifft.

Weil mit jedem Schritt des Igels der Hase einen Schritt näher an den Igel heran kommt, terminiert der Algorithmus in endlicher Zeit.

Performance-Betrachtung

Im besten Fall (best case performance) sind bei einer zyklischen Liste mit m + n Elementen mit n als Länge des Zyklus und m als Anzahl der Elemente vor dem Beginn des Zyklus m Schritte notwendig, da der Igel mindestens den Anfang des Zyklus erreichen muss, bevor der Hase ihn auf einer zweiten Runde einholen kann.

Im schlechtesten Fall (worst case performance) sind m + n Schritte notwendig, das heißt der Hase erreicht den Igel erst auf dem letzten Element der Liste. Zu diesem Zeitpunkt hat der Igel die Schleife genau einmal durchlaufen, der Hase jedoch zweimal.

Implementierungen

C

# include <stdio.h>
# include <stdlib.h>
 
int main() {
        struct liste { struct liste *next; } *root, *el, *hase, *igel;
        int i;
 
        /* Liste erzeugen. */
        root = el = malloc(sizeof(struct liste));
        for(i=0; i<5; ++i) {
                struct liste *eneu = malloc(sizeof(struct liste));
                el->next = eneu;
                el = eneu;
        }
        /* Zyklischen Verweis vom letzten auf das zweite Element anlegen. */
        el->next = root->next;
 
        /* Hase-Igel-Algorithmus. */
        igel = root;
        hase = root->next;
        while(hase && hase != igel) {
                printf("%p %p\n", hase, igel);
                igel = igel->next;
                hase = hase->next;
                if(hase) hase = hase->next;
        }
        if(hase) puts("Zyklus gefunden!");
        else puts("Liste ist nicht zyklisch!");
        return 0;
}

Ada

with Ada.Text_IO; use Ada.Text_IO;
procedure Hase_Igel is
 
   package Int_IO is new Integer_IO(Integer); use Int_IO;
 
   type Liste;
   type Liste_P is access Liste;
   type Liste is record
      Name : Integer;
      Next : Liste_P;
   end record;
 
   Root, Last, Hase, Igel : Liste_P;
 
begin
   -- Liste erzeugen
   Root := new Liste'(Name => 0, Next => null);
   Last := Root;
   for I in 1..12 loop
      Last.Next := new Liste'(Name => I, Next => null);
      Last := Last.Next;
   end loop;
   -- zyklischen Verweis erzeugen
   Last.Next := Root.Next.Next;
 
   -- Hase-Igel-Algorithmus
   Igel := Root;
   Hase := Igel.Next;
   while Hase /= null and Hase /= Igel loop
      Put(Hase.Name, 4); Put(Igel.Name, 4); New_Line;
      Igel := Igel.Next;
      Hase := Hase.Next;
      exit when Hase = null;
      Hase := Hase.Next;
   end loop;
   if Hase = null then
      Put_Line("Liste ist nicht zyklisch");
   else
      Put_Line("Zyklus gefunden");
   end if;
end Hase_Igel;

Vergleich mit anderen Ansätzen zur Schleifenerkennung

Jeden Knoten merken

Ansatz

Jeder durchlaufene Knoten wird in einer geeigneten Struktur gespeichert.

Probleme

• Das Verfahren benötigt sehr viel Speicherplatz und Rechenleistung und ist daher ungeeignet für große Listen.

Doppelte Verkettung nutzen

Ansatz

In einer doppelt verketteten Liste hat jedes Element sowohl einen Zeiger auf das folgende als auch auf das vorhergehende Element. Beim Durchlauf einer solchen Liste muss also jedes Element das vorher besuchte als vorhergehendes Element referenzieren. Wenn das nicht so ist, muss die Liste eine Schleife haben, da – Korrektheit der Verkettung vorausgesetzt – zu diesem besuchten Element zwei Zeiger existieren.

Probleme

• Das Verfahren funktioniert nur, wenn die doppelte Verkettung nicht fehlerhaft ist.
• Eine Schleife über die ganze Liste muss gesondert am Zeiger auf das vorhergehende Element des Startelements geprüft werden.

Jeden Knoten markieren

Ansatz

Die Liste wird durchlaufen; dabei wird jeder Knoten markiert. Wenn ein markierter Knoten getroffen wird, hat die Liste eine Schleife.

Probleme

• Das Verfahren funktioniert nicht, da die Liste im Fall einer Schleife nicht durchlaufen werden kann, um alle Markierungen zu löschen.
• Die Markierung benötigt zusätzlichen Speicherbedarf.

Vergleich mit Startelement

Ansatz

Der Zeiger auf das nächste Element jedes Listenelements wird mit dem Startelement verglichen. Wenn ein Element auf das Startelement zeigt, hat die Liste eine Schleife.

Probleme

• Das Verfahren funktioniert nur bei Listen, die eine einzige Schleife sind. Listen, die an irgendeiner Position nach dem Startelement eine Schleife haben, werden nicht erkannt.

Siehe auch

• Pollard-Rho-Methode
• Primfaktorzerlegung
• Diskreter Logarithmus

Weblinks

• Finding a Loop in a Singly Linked List (englisch)