Primfaktorzerlegung

Die Primfaktorzerlegung ist die Darstellung einer natürlichen Zahl n als Produkt aus Primzahlen, die dann als Primfaktoren von n bezeichnet werden. Diese Darstellung ist (bis auf die Reihenfolge der Faktoren) eindeutig und zählt zu den grundlegenden und klassischen Werkzeugen der Zahlentheorie. Sie ist Gegenstand des Fundamentalsatzes der Arithmetik. Es ist bisher kein effizientes Faktorisierungsverfahren bekannt, um die Primfaktorzerlegung einer beliebigen Zahl zu erhalten.

Definitionen

Sei n eine natürliche Zahl. Eine Zahl p heißt Primfaktor von n,

wenn p ein Teiler von n ist und

p eine Primzahl ist.

Die Primfaktorzerlegung ist die Darstellung der Zahl n als Produkt ihrer Primfaktoren:

$n = p_1 \cdot \ldots \cdot p_N = \prod_{k=1}^{N}p_k$.

Da die Multiplikation kommutativ und assoziativ ist, ist die Reihenfolge der Primfaktoren aus Sicht der Zahlentheorie unwichtig. Da Eins keine Primzahl ist, hat sie auch keinen Primfaktor. Ihre Primfaktorzerlegung kann als leeres Produkt betrachtet werden. Wenn n selbst eine Primzahl ist, so ist es gleichzeitig selbst sein einziger Primfaktor. Gibt es mehr als einen Primfaktor, so wird n zusammengesetzte Zahl genannt. Die Null ist niemals Teil der multiplikativen Gruppe und wird von solchen Betrachtungen ausgeschlossen.

Mehrfach auftretende Primfaktoren können mittels Exponenten-Schreibweise zusammengefasst werden. Sind die Primfaktoren aufsteigend geordnet, spricht man auch von der kanonischen Primfaktorzerlegung:

$n=p_1^{e_1} \cdot \ldots \cdot p_M^{e_M} = \prod_{k=1}^{M} p_k^{e_k}$, wenn unter den N Primfaktoren M verschiedene sind.

Den Exponenten e_k > 0 eines Primfaktors p_k nennt man auch „Vielfachheit von p_k in n“ oder „p_k-Bewertung von n“. Er gibt an, wie oft n durch p_k teilbar ist.

Beispiele für Primfaktorzerlegungen

$30 = 2 \cdot 3 \cdot 5$

$37 = 37 \$ (Primzahl)

$1024 = 2 \cdot \ldots \cdot 2 = 2^{10}$ (Zweierpotenz)

$6936 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 17 \cdot 17$, mit der kanonischen Darstellung $2^3 \cdot 3 \cdot 17^2$

Fundamentalsatz der Arithmetik

Die Aussagen für Existenz der Primfaktorzerlegung für jede natürliche Zahl und deren Eindeutigkeit in der kanonischen Darstellung sind der Fundamentalsatz der Arithmetik. Beide Aussagen werden getrennt formuliert und bewiesen. Die Beweise sind zahlentheoretisch elementar, werden klassisch als Widerspruchsbeweis formuliert und nutzen die Wohlordnung der natürlichen Zahlen. Zum ersten Mal vollständig und korrekt bewiesen findet sich der Fundamentalsatz der Arithmetik in den Disquisitiones Arithmeticae von Carl Friedrich Gauß. Er war aber bereits — wenn auch in leicht abgewandelter Form — Euklid bekannt.

Beweis der Existenz

Der Eins wird das leere Produkt zugeordnet und jede Primzahl stellt selbst ihre Primfaktorzerlegung dar. Damit bleibt zu zeigen, dass alle restlichen natürlichen Zahlen tatsächlich aus Primfaktoren zusammengesetzt sind.

Angenommen, es gibt Zahlen, die sich nicht als Produkt von Primzahlen darstellen lassen, dann gibt es auch eine kleinste solche Zahl (genannt n), aufgrund der Wohlordnung von $\N$. Da n dann weder die Eins noch eine Primzahl ist, besitzt es einen Teiler, damit existieren zwei natürliche Zahlen a,b mit ab = n und beide sind größer als Eins und kleiner als n. Da n die kleinste Zahl ist die kein Produkt von Primfaktoren ist, müssen a und b also Primfaktorzerlegungen haben, etwa a = Πp_i und b = Πq_j. Dann ist aber $\Pi p_i \cdot \Pi q_j$ auch eine Primfaktorzerlegung von n, im Widerspruch zur Annahme.

Beweis der Eindeutigkeit

Angenommen, es gibt natürliche Zahlen mit jeweils mehreren unterschiedlichen Zerlegungen, dann auch wieder eine kleinste, genannt n. Dies kann keine Primzahl sein und zwei Zerlegungen von n können keinen gemeinsamen Primfaktor p enthalten, da dann auch n / p zwei verschiedene Zerlegungen hätte und kleiner als n wäre, im Widerspruch zur Annahme, dass n minimal ist. Es gilt also etwa $n = p \cdot a= q \cdot b$, wobei p und q Primzahlen sind und es gilt $p \neq q, a\neq b$. Das abschließende Argument ist das Lemma von Euklid: Teilt eine Primzahl ein Produkt, so auch einen der Faktoren. Da n durch p teilbar ist, muss einer der Faktoren der anderen Zerlegung durch p teilbar sein und das ist b, denn q ist prim. Also taucht ein beliebiger Primfaktor stets in beiden Zerlegungen auf und damit sind sie identisch.

Eigenschaften

• Bisher lässt die Primfaktorzerlegung von n wenig Rückschluss zu auf die Zerlegung von n + 1, außer dass sie keinen gemeinsamen Teiler haben können. Verwandt mit dieser Frage sind Primzahlzwillinge bzw. Primzahllücken.
• Um die Primfaktorzerlegung einer Zahl zu berechnen, stehen mehrere Faktorisierungsverfahren zur Verfügung, die nichttriviale Teiler ganzer Zahlen berechnen. Diese Aufgabenstellung ist als Faktorisierungsproblem für ganze Zahlen bekannt und kann mit den bisher bekannten Methoden nicht effizient berechnet werden, worauf weltweit Sicherheitskonzepte beruhen, insbesondere in der modernen Kryptographie. Siehe auch Primzahltest.
• Hardy bewies mehrere erstaunliche statistische Erkenntnisse zum Thema, unter anderem, dass die durchschnittliche Anzahl von Primfaktoren für größer werdendes n nur sehr langsam anwächst und zwar wie ln(ln(n)), also der doppelt angewendete natürliche Logarithmus. Der Satz von Erdős-Kac besagt darüber hinaus, dass die Anzahl der Primfaktoren asymptotisch normalverteilt ist mit einem Erwartungswert $\ln \ln n + \mathcal{O}(1)$ und einer Standardabweichung $\mathcal{O}( \sqrt{\ln \ln n})$.^[1] (Zur Notation siehe Landau-Symbole.)
• Der asymptotische arithmetische Mittelwert der maximalen Exponenten der Primfaktorzerlegungen der Zahlen 1, 2, 3, … ist die Niven-Konstante (rund 1,7), der asymptotische arithmetische Mittelwert der minimalen Exponenten ist genau 1.

Verallgemeinerung

Es gibt mehrere Möglichkeiten, Primzahlen zu verallgemeinern. Die bekannteste Anwendung sind die ganzen Zahlen, Primzahlen können dort auch ein negatives Vorzeichen haben. Andererseits ist dies schon ein spezielles Beispiel, da auch dort die Primfaktorzerlegung „bis auf Vorzeichen und Reihenfolge“ eindeutig ist.

Ein allgemeiner Ansatz verlangt mindestens einen Begriff der Teilbarkeit innerhalb der mathematischen Struktur. David Hilbert bewies, dass für die gewünschte Eindeutigkeit eine additive Struktur zwingend notwendig ist. Üblicherweise wird von einem kommutativen Ring mit Eins ausgegangen, dort können Primelemente definiert werden, (für die dann Euklids Lemma gilt), ist der Ring auch noch nullteilerfrei (also ein Integritätsring), kann es zusätzlich irreduzible Elemente geben, die nicht prim genannt werden können. Sie werden anders definiert, sind aber trotzdem unzerlegbar und enthalten die Primelemente als Teilmenge.

Für einen Ring R ist eine Zerlegung in Primelemente einer Zahl $a\in R\setminus\{0\}$ eine Darstellung der Form $a=ep_1^{l_1}p_2^{l_2}\dots p_n^{l_n}$. Dabei ist e eine Einheit, $n\in\mathbb{N}_0, p_i\in R$ paarweise verschiedene Primelemente und $l_i\in \mathbb{N}$ Vielfachheiten. In jedem Ring mit 1 gibt es für jedes von Null verschiedene Element so eine Darstellung. In Hauptidealringen (wie die Polynomringe über Körpern) und euklidischen Ringen (wie $\mathbb{Z}$) kann man zeigen, dass diese Zerlegung bis auf Reihenfolge und Multiplikation mit Einheiten eindeutig ist.

In allgemeinen Integritätsringen ist das nicht immer so. Man muss deren Eindeutigkeit explizit fordern, was zur Definition von faktoriellen Ringen führt. Mit dieser Forderung lässt sich dann aber dort auch schon die Äquivalenz von irreduzibel und prim folgern: Faktorielle Ringe sind ZPE-Ringe. Ein etwas anderer Ansatz wird mit Primidealen verfolgt.

Es gilt dann die Kette von echten Implikationen für Ringe:

$\mbox{Integritätsring}\Leftarrow\mbox{Faktoriell}\Leftarrow \mbox{Hauptideal} \Leftarrow\mbox{Euklidisch}$

Beispiele

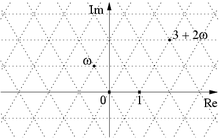Auch auf dem Dreiecksgitter der Eisenstein-Zahlen existiert für jeden Gitterpunkt eine Primfaktorzerlegung

• In dem Integritätsring $\mathbb Z[\sqrt{-5}]$ sind die Elemente $2,3,1+\sqrt{-5}$ irreduzibel und keine zwei sind zueinander assoziiert. Aber es gilt: $6=2\cdot 3=\left(1+\sqrt{-5}\right)\cdot\left(1-\sqrt{-5}\right)$. Man kann also nicht von einer Primfaktorzerlegung sprechen.
• Ein irreduzibles Polynom heißt Primpolynom, wenn der Leitkoeffizient gleich 1 ist. Im Polynomring K[x] über einem Körper K ist jedes nichtkonstante Polynom im Wesentlichen eindeutig als Produkt von Primpolynomen darstellbar.^[2]
• Sowohl in den gaußschen Zahlen als auch den Eisenstein-Zahlen existiert stets eine Primfaktorzerlegung. (außer für die 0)

Praktische Anwendung

Aus der Primfaktorenzerlegung lässt sich erkennen, ob eine Zahl durch eine andere teilbar ist. Das kleinste gemeinsame Vielfache kgV und der größte gemeinsame Teiler ggT können leicht aus der Primfaktorenzerlegung bestimmt werden. In der Bruchrechnung können Brüche durch den ggT von Zähler und Nenner gekürzt werden, und zwei Brüche können auf den kleinsten gemeinsamen Nenner erweitert werden, um leichter addieren oder subtrahieren zu können.

Kryptographie

Eine wichtige Rolle spielen Primzahlen in der Kryptographie. Verschlüsselungssysteme wie RSA basieren darauf, dass kein effizientes Faktorisierungsverfahren bekannt ist. So ist es innerhalb von Sekunden problemlos möglich, zwei 500-stellige Primzahlen zu finden und miteinander zu multiplizieren. Mit den heutigen Methoden würde die Rückgewinnung der beiden Primfaktoren aus diesem 999-stelligen oder 1000-stelligen Produkt dagegen sehr lange Zeit dauern. Primzahlen werden auch bei der Programmierung von Hashtabellen verwendet.

Literatur

• Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. Vieweg, Braunschweig/Wiesbaden 1996, ISBN 3-528-07286-5.

Weblinks

 Wiktionary: Primfaktorzerlegung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Factorization database von Markus Tervooren - schnelle Verarbeitung, bis zu 200.000 Dezimalstellen
• Die Primzahlseite von Arndt Brünner - benötigt JavaScript, enthält u.a. Primfaktorzerlegung
• Prime factorisation by Henry Bottomley (1998) - benötigt JavaScript, verarbeitet Eingaben bis ca. 17 Dezimalstellen
• Factorization using the Elliptic Curve Method - Java-Applet, verarbeitet Eingaben bis 10.000 Dezimalstellen
• WolframAlpha, universeller wissenschaftlich-technischer Taschenrechner

Fußnoten

1. ↑ Thomas Kantke: Billige und teure Zahlen. In: Spektrum der Wissenschaft - SPEZIAL: Omega. Nr. 4/2003, Spektrum der Wissenschaft, Heidelberg 2003, S. 68-74.
2. ↑ Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. Vieweg, Braunschweig/Wiesbaden 1996, ISBN 3-528-07286-5, S. 72, 37.