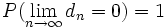Hauptsatz der mathematischen Statistik
Schlagen Sie auch in anderen Wörterbüchern nach:
Theorem der endlos tippenden Affen — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
empirische Verteilung — empirische Verteilung, Stochastik: die der Stichprobe x = (x1, x2,. .., xn) von reellen Beobachtungen zugeordnete diskrete Verteilung h … Universal-Lexikon
Entropie (Thermodynamik) — Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der… … Deutsch Wikipedia
Infinite-Monkey-Theorem — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder einer beliebigen Nationalbibliothek entstehen. Das Infinite Monkey Theorem (engl. infinite „unendlich“, monkey „Affe“ und… … Deutsch Wikipedia
Infinite Monkey Theorem — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
Infinite monkey theorem — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
Information — Das „i“ ist international ein Symbol für Information Information (lat. informare „bilden“, „eine Form, Gestalt, Auskunft geben“) ist eine zeitliche Abfolge von Signalen, deren Sinn und Bedeutung der Empfänger, nach seinen Möglichkeiten und… … Deutsch Wikipedia
Satz vom Affen — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
Unendlich-viele-Affen-Theorem — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
Unendlich-viele-Affen-Theorie — Durch zufälliges Tippen von unendlicher Dauer auf einer Schreibmaschine werden mit Sicherheit alle Texte Shakespeares oder diverser Nationalbibliotheken entstehen. Das Infinite Monkey Theorem (v. engl. infinite „unendlich“; monkey „Affe“; theorem … Deutsch Wikipedia
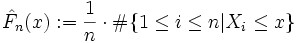die enstsprechende empirische Verteilungsfunktion (hierbei gibt wie üblich das Rautensymbol 
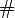die Anzahl der Elemente der darauf folgenden Menge an).
.
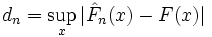