Hidden Markov Model

Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Es ist die einfachste Form eines dynamischen Bayes'schen Netzes.

Der erste Zufallsprozess entspricht dabei einer Markov-Kette, die durch Zustände und Übergangswahrscheinlichkeiten gekennzeichnet ist. Die Zustände der Kette sind von außen jedoch nicht direkt zu beobachten (sie sind hidden, verborgen). Stattdessen erzeugt ein zweiter Zufallsprozess zu jedem Zeitpunkt beobachtbare Ausgangssymbole (oder Beobachtungen) gemäß einer zustandsabhängigen Wahrscheinlichkeitsverteilung. Das Attribut verborgen bezieht sich bei einem Hidden Markov Model auf die Zustände der Markow-Kette während der Ausführung, nicht auf die Parameter des Markow-Modells. Die Aufgabe besteht meist darin, aus der Sequenz der Ausgabesymbole (Beobachtungen) auf die Sequenz der verborgenen Zustände zu schließen.

Wichtige Anwendungsgebiete sind neben der Spracherkennung (und allgemein Computerlinguistik) und der Bioinformatik unter anderem Spamfilter (insbesondere Markow-Filter), Gestenerkennung in der Mensch-Maschine-Kommunikation (Robotik), Schrifterkennung und Psychologie.

Definition

Parameter eines Hidden Markov Modell (Beispiel)
x — (verborgene) Zustände
y — mögliche Beobachtungen (Emissionen)
a — Übergangswahrscheinlichkeiten
b — Emissionswahrscheinlichkeiten

Formal definiert man ein HMM als Quintupel λ = (X,A,Y,B,π) mit

• X = {x₁,...,x_n} – Menge aller Zustände
• A = {a_ij} – Zustandsübergangsmatrix, wobei a_ij die Wahrscheinlichkeit angibt, dass von Zustand x_i in Zustand x_j gewechselt wird.
• Y = {y₁,...,y_m} – Menge der möglichen Beobachtungen (Emissionen)
• B = {b_ij} – Beobachtungsmatrix wobei b_ij die Wahrscheinlichkeit angibt, im Zustand x_i die Beobachtung $y_{j} \in Y$ zu machen
• π – Anfangswahrscheinlichkeitsverteilung mit π(i) Wahrscheinlichkeit, dass x_i der Startzustand ist

Ein HMM ist stationär (o. a. zeitinvariant) wenn sich die Übergangs- und Emissionswahrscheinlichkeiten nicht mit der Zeit ändern. Diese Annahme ist oft sinnvoll, weil auch die modellierten Naturgesetze konstant sind. Im Normalfall sind die unterliegenden Markow-Ketten erster Ordnung (o. a. Horizont), das heißt der aktuelle Zustand hängt nur von genau einem vorherigen Zustand ab.

Veranschaulichung

Zeitliche Entwicklung eines HMM

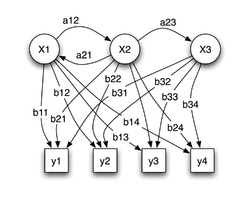
Das Bild zeigt die generelle Architektur eines instantiierten HMMs. Jedes Oval ist die Repräsentation einer zufälligen Variable, welche beliebige Werte aus X bzw. Y annehmen kann. Die Zufallsvariable x(t) ist der versteckte Zustand des HMMs zum Zeitpunkt t. Die Zufallsvariable y(t) ist die Beobachtung zum Zeitpunkt t. Die Pfeile in dem Trellis-Diagramm bedeuten eine bedingte Abhängigkeit.

Im Diagramm sieht man, dass der Zustand der versteckten Variable x(t) zum Zeitpunkt t nur vom Zustand der Variable x(t − 1) abhängt, frühere Werte haben keinen weiteren Einfluss. Deshalb ist das Modell ein Markow-Modell 1. Ordnung. Wenn höhere Ordnungen gebraucht werden, können diese durch das Einfügen neuer versteckter Zustände auf die 1. Ordnung zurückgeführt werden. Der Wert von y(t) hängt von x(t) ab.

Beispiel

Gefangener im Verlies

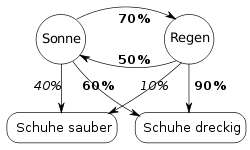
Ein Gefangener im Kerkerverlies möchte das aktuelle Wetter herausfinden. Er weiß, dass auf einen sonnigen Tag zu 70 % ein Regentag folgt und dass auf einen Regentag zu 50 % ein Sonnentag folgt. Weiß er zusätzlich, dass die Schuhe der Wärter bei Regen zu 90 % dreckig, bei sonnigem Wetter aber nur zu 60 % dreckig sind, so kann er durch Beobachtung der Wärterschuhe Rückschlüsse über das Wetter ziehen.

DNA-Sequenz: CpG-Inseln aufspüren

Zur Untersuchung von DNA-Sequenzen mit bioinformatischen Methoden kann das HMM verwendet werden. Beispielsweise lassen sich so CpG-Inseln in einer DNA-Sequenz aufspüren. Dabei stellt die DNA-Sequenz die Beobachtung dar, deren Zeichen {A,C,G,T} bilden das Ausgabealphabet. Im einfachsten Fall besitzt das HMM zwei verborgene Zustände, nämlich CpG-Insel und nicht-CpG-Insel. Diese beiden Zustände unterscheiden sich in ihrer Ausgabeverteilung, so dass zum Zustand CpG-Insel mit größerer Wahrscheinlichkeit Zeichen C und G ausgegeben werden.

Problemstellungen

Im Zusammenhang mit HMMs existieren mehrere grundlegende Problemstellungen^[1][2].

Bestimmen der Modellgröße

Gegeben sind die beobachtbaren Zustände. Es ist zu klären, welche Modelleigenschaften, insbesondere welche orthogonale Dimensionalität den Schluss auf die nicht direkt beobachtbaren Zustände erlauben und gleichzeitig eine sinnvolle Berechenbarkeit zulassen. Insbesondere ist zu entscheiden, welche Laufzeit für die Modellrechnungen erforderlich werden darf, um die Verwendbarkeit der Schätzungen zu erhalten.

Implementierung

Die Berechnung der Schätzwerte der nicht beobachtbaren Zustände aus den beobachtbaren Zustandsvektoren muss die erreichbaren numerischen Genauigkeiten beachten. Weiter müssen Kriterien zur Klassifizierung der statistischen Signifikanz implementiert werden. Bei Verwendung eines HMM für einen bestimmten Merkmalsvektor bestimmt die statistische Signifikanz die Wahrscheinlichkeit einer zutreffenden oder falschen Modellhypothese sowie deren Informationsgehalt (Entropie, Bedingte Entropie) bzw. deren Informationsqualität.

Filtern

Gegeben ist ein HMM λ sowie eine Beobachtungssequenz Y_1:t. Gesucht ist die Wahrscheinlichkeit P(X_t | Y_1:t), d.h. der momentane verborgene Zustand X zum Zeitpunkt t. Ein effizientes Verfahren zur Lösung des Evaluierungsproblems ist der Forward-Algorithmus.

Prädiktion/Vorhersage

Gegeben ist ein HMM λ und die Beobachtungssequenz Y_1:t. Gesucht ist Wahrscheinlichkeit P(X_{t + δ} | Y_1:t), also die Wahrscheinlichkeit, dass sich das HMM zum Zeitpunkt t + δ im Zustand X befindet unter der Bedingung, dass die Ausgabe Y beobachtet wurde. Prädiktion ist quasi wiederholtes Filtern ohne neue Beobachtungen und lässt sich auch einfach mit dem Forward-Algorithmus berechnen (Problem Nr. 1 in der angegebenen Quelle).

Glätten

Gegeben ist ein HMM λ und die Beobachtungssequenz Y_1:t Gesucht ist die Wahrscheinlichkeit P(X_{t − δ} | Y_1:t), also die Wahrscheinlichkeit, dass sich das Modell zu einem früheren Zeitpunkt im Zustand X befand, unter der Bedingung, dass Y beobachtet wurde. Mit Hilfe des Backward-Algorithmus kann diese Wahrscheinlichkeit effizient berechnet werden.

Dekodierungsproblem

Gegeben ist ein HMM λ und die Beobachtungssequenz Y_1:t. Es soll die wahrscheinlichste Sequenz der (versteckten, hidden) Zustände bestimmt werden, die eine vorgegebene Ausgabesequenz erzeugt hat. Lösbar mit Hilfe des Viterbi-Algorithmus (Problem Nr. 2 in der angegebenen Quelle).

Lernproblem

Gegeben ist nur die Ausgabesequenz. Es sollen die Parameter des HMM bestimmt werden, die am wahrscheinlichsten die Ausgabesequenz erzeugen. Lösbar mit Hilfe des Baum-Welch-Algorithmus (Problem Nr. 3 in der angegebenen Quelle).

Interpretationsproblem

Gegeben ist nur der beobachtbare Zustandsvektor. Es sollen die Zustände im Modellsystem und die korrespondierenden Effekte im realen System identifiziert werden, die der Zustandsvektor des Modells beschreibt^[3]. Dazu muss vorweg die Bedeutsamkeit der Elemente der Merkmalsvektoren bestimmt werden.

Anwendungsgebiete

Anwendung finden HMMs häufig in der Mustererkennung bei der Verarbeitung von sequentiellen Daten, beispielsweise bei physikalischen Messreihen, aufgenommenen Sprachsignalen oder biologischen Sequenzen. Dazu werden die Modelle so konstruiert, dass die verborgenen Zustände semantischen Einheiten entsprechen (z. B. Phoneme in der Spracherkennung), die es in den sequentiellen Daten (z. B. Kurzzeit-Spektren des Sprachsignals) zu erkennen gilt. Eine weitere Anwendung besteht darin, für ein gegebenes HMM durch eine Suche in einer Stichprobe von sequentiellen Daten solche Sequenzen zu finden, die sehr wahrscheinlich von diesem HMM erzeugt sein könnten. Beispielsweise kann ein HMM, das mit Vertretern einer Proteinfamilie trainiert wurde, eingesetzt werden, um weitere Vertreter dieser Familie in großen Proteindatenbanken zu finden.

Geschichte

Hidden Markov Modelle wurden erstmals von Leonard E. Baum und anderen Autoren in der zweiten Hälfte der 1960er Jahre publiziert. Eine der ersten Applikationen war ab Mitte der 1970er die Spracherkennung. Seit Mitte der 1980er wurden HMMs für die Analyse von DNA-Sequenzen und Proteinsequenzen eingesetzt und sind seitdem fester Bestandteil der Bioinformatik.

Literatur

1. ↑ Lawrence R. Rabiner: A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE, Band 77, Nr. 2, S. 257–286, 1989; 2,2 MB
2. ↑ Phil Blunsom, Hidden Markov Models
3. ↑ S.P. Chatzis, A Variational Bayesian Methodology for Hidden Markov Models

• Rainer Merkl, Stephan Waack: Bioinformatik interaktiv. Wiley-VCH, 2002, ISBN 3-527-30662-5.
• Gernot A. Fink: Mustererkennung mit Markov-Modellen: Theorie, Praxis, Anwendungsgebiete. Teubner, 2003, ISBN 3-519-00453-4
• Kai-Fu Lee, Hsiao-Wuen Hon: Speeker-Independent Phone Recognition Using Hidden Markov Models. IEEE Transactions on accoustics, speech and signal processing, Nr. 37, IEEE, November 1989, S. 1641-1648 (IEEE Nr. 8930533, 0096-3518/89/1100-1641).

Weblinks

• HMM R-Package zum Modellieren und Analysieren von Hidden Markov Modellen, das unter GPL2 frei verfügbar ist
• http://code.google.com/p/jahmm/ HMM Java-Bibliothek, die unter der neuen BSD-Lizenz verfügbar ist.
• http://www.ghmm.org HMM C-Bibliothek, die unter der LGPL frei verfügbar ist