Zufallsprozess

Zufallsprozess
Die Brownsche Brücke, ein stochastischer Prozess

Ein Stochastischer Prozess ist die mathematische Beschreibung von zeitlich geordneten, zufälligen Vorgängen. Die Theorie der stochastischen Prozesse stellt eine wesentliche Erweiterung der Wahrscheinlichkeitstheorie dar und bildet die Grundlage für die stochastische Analysis. Obwohl einfache stochastische Prozesse schon vor langer Zeit studiert wurden, wurde die heute gültige formale Theorie erst anfang des 20. Jahrhunderts entwickelt, vor allem durch Paul Lévy und Andrei Nikolajewitsch Kolmogorow.

Inhaltsverzeichnis

Definition

Sei 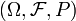(\Omega, \mathcal{F}, P) ein Wahrscheinlichkeitsraum, 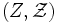(Z, \mathcal{Z}) ein mit einer Sigma-Algebra versehener Raum (zumeist die reellen Zahlen mit der Borelschen Sigma-Algebra) und T eine Indexmenge, zumeist 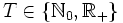T \in \{ \N_0,\R_{+} \} . Ein stochastischer Prozess X ist dann eine Familie von Zufallsvariablen 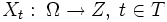X_t:\;\Omega \to Z,\;t\in T, also eine Abbildung

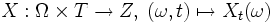X:\Omega \times T \to Z, \; (\omega, t) \mapsto X_t(\omega),

sodass für alle 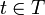t \in T die eingeschränkte Abbildung 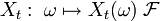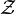X_t:\;\omega \mapsto X_t(\omega)\; \mathcal{F}-\mathcal{Z}-messbar ist. Eine alternative Formulierung sieht vor, dass X eine einzige Zufallsvariable 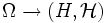\Omega \to (H, \mathcal{H}) ist, wobei 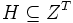H \subseteq Z^T eine (mit einer geeigneten Sigma-Algebra versehene) Menge von Funktionen 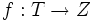f: T \to Z ist. Bei geeigneter Wahl fallen diese beiden Definitionen zusammen.

Einteilung

Die grundlegendste Einteilung stochastischer Prozesse in verschiedene Klassen erfolgt über die Indexmenge T und die Wertemenge Z:

  • Ist T abzählbar (etwa 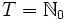T=\N_0), so heißt der Prozess zeitdiskret, ansonsten zeitstetig.
  • Ist Z endlich oder abzählbar, spricht man von wertediskreten Prozessen oder Punktprozessen.

Darüber hinaus werden stochastische Prozesse noch nach stochastischen Eigenschaften in verschiedene Prozessklassen unterteilt. Die wichtigste Klasse ist hierbei die der Markow-Prozesse, die sich durch eine Art „Gedächtnislosigkeit“ auszeichnen. Die meisten untersuchten Prozesse gehören dieser Klasse an. Innerhalb der Markow-Prozesse (im zeitdiskreten Fall spricht man auch von Markow-Ketten) sind wiederum die Lévy-Prozesse von Bedeutung, die ein stochastisches Äquivalent zu den linearen Abbildungen darstellen. Weitere Prozessklassen sind Martingale, Gauß-Prozesse und Ito-Prozesse

Stochastische Prozesse versus Zeitreihen

Neben der Theorie der stochastischen Prozesse gibt es auch die mathematische Disziplin der Zeitreihenanalyse, die weitgehend unabhängig davon operiert. Definitionsgemäß sind stochastische Prozesse und Zeitreihen ein und dasselbe, dennoch weisen die Gebiete Unterschiede auf: Während die Zeitreihenanalyse sich als Teilgebiet der Statistik versteht und versucht, spezielle Modelle (wie etwa ARMA-Modelle) an zeitlich geordnete Daten anzupassen, steht bei den stochastischen Prozessen die Stochastik und die spezielle Struktur der Zufallsfunktionen (etwa Stetigkeit, Differenzierbarkeit, Variation oder Messbarkeit bezüglich gewisser Filtrierungen) im Vordergrund.

Beispiele

Ein Standard-Wiener-Prozess auf den Zeitintervall [0,3], außerdem sind die Varianz und die Standardabweichung eingezeichnet
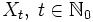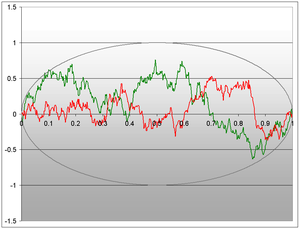
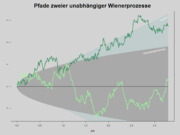
  • Ein einfaches Beispiel für einen zeitdiskreten Punktprozess ist der symmetrische Random Walk, hier veranschaulicht durch ein Glücksspiel: ein Spieler beginnt zum Zeitpunkt t=0 mit einem Startkapital von 10 Euro ein Spiel, bei dem er nacheinander immer wieder eine Münze wirft. Bei „Kopf“ gewinnt er einen Euro, bei „Zahl“ verliert er einen. Der Kontostand X_t,\;t \in \N_0nach t Spielen ist nun ein stochastischer Prozess (mit deterministischer Startverteilung X0 = 10). Genauer betrachtet handelt es sich bei X um einen Lévy-Prozess und um ein Martingal.
  • Der in der Theorie wichtigste stochastische Prozess ist sicherlich der Wiener-Prozess (auch „Brownsche Bewegung“ genannt). Hierbei sind die einzelnen Zustände normalverteilt mit linear anwachsender Varianz. Der Wiener-Prozess findet Anwendung in der stochastischen Integration, der Finanzmathematik und der Physik.

Weblinks


Wikimedia Foundation.

Игры ⚽ Нужен реферат?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • HMM — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden-Markov-Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden Markov Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden Markov model — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Verborgenes Markow-Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Verdecktes Markow-Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Verstecktes Markow-Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden Markov Model — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Es ist die einfachste Form eines dynamischen Bayes schen Netzes. Der erste Zufallsprozess entspricht dabei einer Markov Kette, die …   Deutsch Wikipedia

  • Wiener-Chintschin-Theorem — Das Wiener Chintschin Theorem, auch bekannt als Wiener Chintchin Kriterium oder Chintschin Kolmogorow Theorem, besagt, dass die spektrale Leistungsdichte eines „stationären[1] Zufallsprozesses“ die Fourier Transformation der korrespondierenden… …   Deutsch Wikipedia

  • Anatolij Skorochod — Anatoli Volodymyrowytsch Skorochod (ukrainisch Анатолій Володимирович Скороход, wiss. Transliteration Anatolij Volodymyrovyč Skorochod; * 10. September 1930 in Nikopol) ist ein ukrainischer Mathematiker und seit 1985 Akademiemitglied der… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”