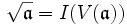Hilberts Nullstellensatz

Der Hilbertsche Nullstellensatz stellt in der Mathematik in der klassischen algebraischen Geometrie die zentrale Verbindung zwischen Idealen und affinen algebraischen Varietäten her. Er wurde von David Hilbert bewiesen. Es gibt verschiedene äquivalente Varianten, den Nullstellensatz zu formulieren:

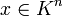• Ist K ein algebraisch abgeschlossener Körper und $\mathfrak a\subsetneq K[X_1,\ldots,X_n]$ ein echtes Ideal, so gibt es ein $x\in K^n$, so dass

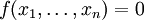$f(x_1,\ldots,x_n)=0$ für alle $f\in\mathfrak a$.

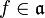x ist also eine gemeinsame Nullstelle aller Elemente von $\mathfrak a$.

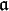• Ist K ein algebraisch abgeschlossener Körper und 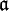$\mathfrak{a}$ ein Ideal in $K[X_1, \dots, X_n]$, dann gilt:

$\sqrt{\mathfrak{a}} = I(V(\mathfrak{a}))$

Hierbei bedeutet

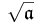• $\sqrt{\mathfrak{a}}$ das Radikal von $\mathfrak{a}$,
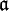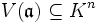• $V(\mathfrak a)\subseteq K^n$ die Menge aller gemeinsamen Nullstellen von 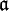$\mathfrak{a}$ (wie oben), und
• I(X) das Ideal aller Polynome, die auf 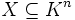$X\subseteq K^n$ verschwinden.

Die Inklusion 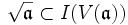$\sqrt{\mathfrak{a}} \subset I(V(\mathfrak{a}))$ ist dabei trivial, denn jede Nullstelle von f(T)^r ist auch Nullstelle von f(T).

Der Hilbertsche Nullstellensatz liefert also eine bijektive Beziehung (Bijektion) zwischen affinen algebraischen Mengen und Radikalidealen. Dass dies nur für Radikalideale gelten kann, ergibt sich aus $V(\sqrt{\mathfrak a})=V(\mathfrak a)$.

• Es sei K ein Körper und 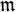$\mathfrak m$ ein maximales Ideal in $A=K[X_1,\ldots,X_n]$. Dann ist der Grad der Körpererweiterung $[A/\mathfrak m:K]$ endlich.

• Es sei K ein Körper und L / K eine Körpererweiterung, die als K-Algebra endlich erzeugt ist. Dann ist [L:K] endlich; insbesondere ist die Erweiterung algebraisch.

Weblinks