Hydrostatisches Paradoxon

Der Flüssigkeitsdruck am Boden (rot; alle gleich groß) ist in allen drei Gefäßen paradoxerweise identisch, obwohl der "normale" Menschenverstand erwartet, dass er im linken Gefäß geringer ist als im rechten.

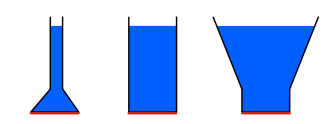
Das Hydrostatische Paradoxon (auch Pascalsches Paradoxon) ist das Paradoxon, dass der Schweredruck, den eine Flüssigkeit in einem Gefäß auf den Boden des Gefäßes bewirkt, zwar abhängig von der Füllhöhe der Flüssigkeit, aber nicht von der Form des Gefäßes und damit der Flüssigkeitsmenge in ihm ist. Die physikalische Grundlage ist der hydrostatische Druck. Er errechnet sich zu:

$p(h) = \rho \, g \, h$

mit:

p(h) – Hydrostatischer Druck in Anhängigkeit von der Höhe des Flüssigkeitsspiegels

g – Erdbeschleunigung (für Deutschland: g ≈ 9,81 m/s²)

ρ – Dichte (für Wasser: ρ ≈ 1000 kg/m³)

h – Höhe des Flüssigkeitsspiegels ^[1]

Erläuterung

In allen Gefäßen mit demselben Füllstand wirkt in derselben Höhe derselbe Flüssigkeitsdruck auf den Gefäßboden, unabhängig von der Grundfläche und der Gefäßgeometrie. Als Konsequenz stellt sich bei Kommunizierenden Röhren derselbe Pegel ein, unabhängig von der Röhrengeometrie.

• 

  In allen Gefäßen herrscht in derselben Höhe derselbe Druck.

• 

  Kommunizierende Röhren: In allen Röhren herrscht derselbe Flüssigkeitsstand, obwohl sich die Flüssigkeitsmengen stark unterscheiden.

Ein normales, intaktes Fass wurde bei diesem historischen Versuch (von Pascal, 1648) durch die Wassersäule (bis zur 2. Etage) in einem langen, dünnen Rohr undicht, was den enormen Wasserdruck demonstrierte.

Für eine ruhende Flüssigkeit in einem homogenen Schwerefeld unter Vernachlässigung des Kapillareffekts ist der hydrostatische Druck nur von der Tiefe unter der Flüssigkeitsoberfläche abhängig. Wäre der Wasserstand in verschiedenen aufsteigenden Ästen der kommunizierenden Röhren verschieden, wäre die Flüssigkeit in ihnen nicht im Gleichgewicht. In diesem Fall fließt die Flüssigkeit in den Querverbindungen, bis (bei Vorhandensein von Reibung) ein Gleichgewicht hergestellt ist. Danach steht die Flüssigkeit in allen Ästen gleich hoch. Der Luftdruck muß keine Berücksichtigung finden, da er in sehr guter Näherung im gesamten Bereich der kommunizierenden Röhren gleich hoch ist.

In einem Gefäß mit Flüssigkeit heben sich die durch die Flüssigkeit verursachten Kräfte und die Gegenkräfte der Gefäßwand auf. Dieses Kräftegleichgewicht kann verwendet werden, um zu veranschaulichen, wie die verschiedenen Kräfte wirken, obwohl in derselben Tiefe überall derselbe hydrostatische Druck herrscht. An einer Grenzfläche zwischen der Flüssigkeit und dem Gefäß steht die Flüssigkeit an jedem Punkt, genauso wie im Inneren der Flüssigkeit, unter einem bestimmten hydrostatischen Druck p(h) abhängig von der Tiefe h unter dem Flüssigkeitsspiegel. Das verursacht eine Kraft auf jedes Flächenstück, die senkrecht auf das Flächenstück und nach außen wirkt. Solange die Gefäßwand intakt ist, bewirkt sie einen Gegendruck, der die Kraftwirkung des hydrostatischen Drucks aufhebt. Bricht an einer Stelle, an der im Gefäß ein hydrostatischer Druck über null herrscht, eine Öffnung auf, tritt an dieser Stelle Flüssigkeit aus und wird durch die Kräfte aufgrund der Druckdifferenz beschleunigt. Infolgedessen spritzt die Flüssigkeit von der Öffnung weg, je nach Lage der Öffnung auch nach oben. Nach dem Austritt aus der Öffnung wirkt kein kydrostatischer Druck mehr auf die Flüssigkeit, und infolgedessen auch keinerlei Kraft aufgrund des hydrostatischen Drucks.

Erklärung des Effektes in Kommunizierenden Röhren

Kräfte in den Kommunizierenden Röhren:
 grün: Kraft durch den Luftdruck;
 blau: Schwerekraft des Wassers;
 braun: Gegenkraft des Wassers in der Querröhre;
 magenta: Kraft, mit der die Gefäßhülle der Belastung entgegenwirken muss.

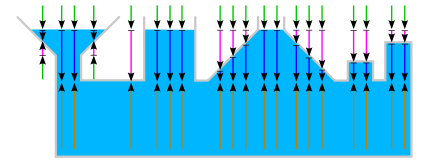
Der Trichter und Zylinder entfalten an ihren Bodenflächen jeweils die Gegenkraft aus der Gewichtskraft des darüber liegenden Wassers (blau) plus die Kraft durch den Luftdruck (grün).

Die Gegenkraft des Wassers der Querröhre (braun) ist bei allen Bodenflächen der nun zusammengesetzten Röhren gleich. Dies ist gleichbedeutend mit der Aussage, dass der Wasserdruck auf gleicher Höhe den gleichen Betrag aufweist.

Die Kräfte am Randbereich des Trichters wirken auf die Gefäßhülle und diese trotzt der Belastung mit einer ebenso großen Gegenkraft (magenta), da sonst die Hülle brechen würde. Genauso muss die Hülle des Kegels den Kräften entgegenwirken, die auf Grund der geringeren Wassermenge und der daraus resultierenden geringeren Gewichtskraft nur abgeschwächt und nicht aufgehoben werden.

An den rechten zwei verschlossenen Röhren sieht man deutlich, dass die Kraft auf die Hülle und die gleiche Gegenkraft der Hülle abhängig von der Höhe sind. Verschließt man den Trichter in der Höhe des Wasserstandes mit einem hauchdünnen Deckel, kann dieser nicht brechen. Setzt man diesen Deckel jedoch etwas tiefer an und entfernt das über ihm liegende Wasser, so bricht dieser, da er die notwendige Gegenkraft nicht aufbauen kann.

Anwendung

• Ein Wasserturm ist ein Reservoir, das höher platziert ist als die Wasserverbraucher. Der Höhenunterschied bewirkt den Wasserdruck bei den Abnahmestellen.
• Die Schlauchwaage ist ein ideales Instrument zum Abmessen von Höhenunterschieden an weit entfernten Orten. Das Funktionsprinzip beruht auf den Kommunizierenden Röhren: Der Wasserstand ist in beiden senkrecht aufgestellten Enden eines Schlauches gleich hoch.
• Beim Artesischen Brunnen tritt an einem Brunnenloch das Wasser von selbst nach oben.
• alle hydraulischen Geräte

Einzelnachweise

1. ↑ L. D. Landau, E. M. Lifschitz: Statistische Physik Teil I, Akademie Verlag Berlin 1979/1987, ISBN 3-05-500069-2, S. 70

Literatur

• Wolfgang Demtröder: Experimentalphysik 1 - Mechanik und Wärme. 2. Auflage. Springer-Verlag, Berlin, Heidelberg, New York 2001, ISBN 3-540-64292-7
• Willi Bohl, Wolfgang Elmendorf: Technische Strömungslehre. 13. Auflage. Vogel-Buchverlag, Würzburg, ISBN 3-8343-3029-9

Weblinks

 Commons: Hydrostatisches Paradoxon – Sammlung von Bildern, Videos und Audiodateien

• Video von Kommunizierenden Röhren