Alternierende Multilinearform
- Alternierende Multilinearform
-
Eine p-Multilinearform ω ist in der Mathematik eine Funktion, die p Argumenten  aus K-Vektorräumen
aus K-Vektorräumen  einen Wert
einen Wert  zuordnet und in jeder Komponente linear ist.
zuordnet und in jeder Komponente linear ist.
Multilinearformen
Eine Abbildung
 ,
,
welche für alle  ,
, 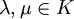 und
und  für festes, beliebiges
für festes, beliebiges 

erfüllt, heißt multilineare Abbildung. Die Menge aller multilinearen Abbildungen  bildet einen K-Vektorraum. Im Fall
bildet einen K-Vektorraum. Im Fall  schreibt man
schreibt man  .
.
Alternierende Multilinearformen
Eine Multilinearform  heißt alternierende Multilinearform, falls sie bei Vertauschung von je zwei Argumenten ihr Vorzeichen wechselt, d.h.
heißt alternierende Multilinearform, falls sie bei Vertauschung von je zwei Argumenten ihr Vorzeichen wechselt, d.h.

für alle  und
und  .
.
Die Menge aller alternierenden Multilinearformen Ωp(V) ist ein Unterraum von  .
.
Wichtig ist der Spezialfall  . Dann ist
. Dann ist  ein 1-dimensionaler Unterraum von
ein 1-dimensionaler Unterraum von  , und seine Elemente heißen Determinantenfunktionen.
, und seine Elemente heißen Determinantenfunktionen.
Beispiele
- 1. Linearformen (Skalarprodukt mit vorgegebenem Vektor) sind genau die 1-Multilinearformen.
- 2. Bilinearformen sind genau die 2-Multilinearformen. Antisymmetrische Bilinearformen sind alternierende Multilinearformen.
- 3. Bildet man aus n Vektoren durch Zusammenfassen eine quadratische Matrix, so ist die Determinante dieser Matrix eine alternierende, normierte Multilinearform. Im dreidimensionalen Fall ist also ω definiert durch

- eine alternierende 3-Multilinearform. Dabei sind die Vektoren v1,v2,v3 folgendermaßen in Koordinaten dargestellt:
 .
.
- 4. Kovariante Tensoren sind Multilinearformen: In dem Fall, dass alle Vektorräume Vi identisch sind (also Vi = V), ist die p-Multilinearform auch ein kovarianter Tensor p-ter Stufe. Im selben Fall sind die alternierenden p-Multilinearformen auch total antisymmetrische Tensoren p-ter Stufe.
Verallgemeinerung
Es seien Moduln 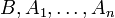 über einem kommutativen Ring R gegeben. Eine Abbildung
über einem kommutativen Ring R gegeben. Eine Abbildung  heißt multilineare Abbildung, wenn sie in jeder Komponenten linear ist, d.h., für alle
heißt multilineare Abbildung, wenn sie in jeder Komponenten linear ist, d.h., für alle  und alle
und alle  ist
ist

ein R-Modulhomomorphismus.
Multilinearformen sind spezielle multilineare Abbildungen, für die nämlich R ein Körper und B = R ist.
Multilineare Abbildungen werden benötigt, um das Tensorprodukt mittels der folgenden universellen Eigenschaft zu definieren, und sie werden damit zugleich klassifiziert: Für jede multilineare Abbildung  gibt es genau einen Homomorphismus
gibt es genau einen Homomorphismus  , so dass das folgende Diagramm kommutiert:
, so dass das folgende Diagramm kommutiert:

Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Multilinearform — Eine p Multilinearform ω ist in der Mathematik eine Funktion, die p Argumenten aus K Vektorräumen einen Wert zuordnet und in jeder Komponente linear ist. Im allgemeineren Fall, dass der Bildraum selbst ein Vektorraum ist, oder Bild und Zielräume… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Integrabel — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kollinear — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kopunktal — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Mathematisches Attribut — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Multivariat — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Primitives Element — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
 aus K-Vektorräumen
aus K-Vektorräumen  einen Wert
einen Wert  zuordnet und in jeder Komponente linear ist.
zuordnet und in jeder Komponente linear ist. ,
, ,
, 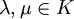 und
und  für festes, beliebiges
für festes, beliebiges 
 bildet einen K-Vektorraum. Im Fall
bildet einen K-Vektorraum. Im Fall  schreibt man
schreibt man  .
. heißt alternierende Multilinearform, falls sie bei Vertauschung von je zwei Argumenten ihr Vorzeichen wechselt, d.h.
heißt alternierende Multilinearform, falls sie bei Vertauschung von je zwei Argumenten ihr Vorzeichen wechselt, d.h. und
und  .
. .
. . Dann ist
. Dann ist  ein 1-dimensionaler Unterraum von
ein 1-dimensionaler Unterraum von  , und seine Elemente heißen Determinantenfunktionen.
, und seine Elemente heißen Determinantenfunktionen. .
.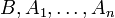 über einem kommutativen Ring R gegeben. Eine Abbildung
über einem kommutativen Ring R gegeben. Eine Abbildung  heißt multilineare Abbildung, wenn sie in jeder Komponenten linear ist, d.h., für alle
heißt multilineare Abbildung, wenn sie in jeder Komponenten linear ist, d.h., für alle  und alle
und alle  ist
ist gibt es genau einen Homomorphismus
gibt es genau einen Homomorphismus  , so dass das folgende Diagramm kommutiert:
, so dass das folgende Diagramm kommutiert:




