Tensorprodukt

Das Tensorprodukt ist ein sehr vielseitiger Begriff der Mathematik: in der linearen Algebra und der Differentialgeometrie dient es der Beschreibung von multilinearen Abbildungen, in der kommutativen Algebra und algebraischen Geometrie entspricht es einerseits der Einschränkung geometrischer Strukturen auf Teilmengen, andererseits dem kartesischen Produkt geometrischer Objekte.

Dieser Artikel beschreibt die mathematischen und koordinatenfreien Aspekte des Tensorproduktes. Für einzelne Tensoren und Koordinatendarstellungen siehe Tensor.

Tensorprodukt von Vektorräumen

Sind V und W zwei Vektorräume über einem gemeinsamen Skalarkörper K, so ist das Tensorprodukt

$V\otimes W$

ein Vektorraum, der wie folgt konstruiert werden kann: Ist $E=\{e_i\mid i\in I\}$ eine Basis von V und $F=\{f_j\mid j\in J\}$ eine Basis von W, dann ist $V\otimes W$ ein Vektorraum, in dem es eine Basis gibt, die auf eindeutige Weise mit den geordneten Paaren des kartesischen Produkts

$E\times F=\{(e_i,f_j)\mid i\in I, j\in J\}$

der Basen der Ausgangsräume identifiziert werden kann. Die Dimension von $V\otimes W$ ist demzufolge gleich dem Produkt der Dimensionen von V und W.

Das Element dieser Basis, das dem geordneten Paar (e_i,f_j) entspricht, wird als $e_i\otimes f_j$ notiert. Das Symbol $\otimes$ hat dabei bis hier keine tiefere Bedeutung. Man kann nun mit Hilfe dieser Basis ein Produkt von Vektoren aus V und W definieren, welches mit demselben Verknüpfungssymbol notiert wird. Natürlicherweise ist das Produkt zweier Basisvektoren $e_i\in E\subset V$ und $f_j\in F\subset W$ gerade der Basisvektor, der mit $e_i\otimes f_j\in V\otimes W$ bezeichnet wurde. Das Produkt beliebiger Vektoren kann nun durch bilineare Fortsetzung erhalten werden,

$v=\sum_{i\in I_0}a_ie_i\in V$ und $w=\sum_{j\in J_0}b_jf_j\in W$ – mit $I_0\subset I,\;J_0\subset J$ endlich –

wird das Produkt

$v\otimes w=\sum_{(i,j)\in I_0\times J_0} a_ib_j\;(e_i\otimes f_j)$

zugeordnet.

Für endlichdimensionale Vektorräume V und W kann das Tensorprodukt direkt als Raum von Matrizen konstruiert werden. Die Zeilen werden mit dem Basisindex $I=\{1,\dots,m\}$ von V nummeriert, die Spalten mit dem Basisindex $J=\{1,\dots,n\}$ von W. Das Produkt zweier Vektoren $v\in V,\;w\in W$ ist diejenige Matrix, deren Eintrag an der Stelle (i,j) die i-te Koordinate von v mal der j-ten Koordinate von w ist. Die Spalten sind Vielfache von v, die Zeilen sind Vielfache von w. (In der Sprache der Matrizen nennt sich diese Konstruktion auch dyadisches Produkt.)

Für das Symbol $v\otimes w$ gelten folgende Rechenregeln:

• $(v'+v'')\otimes w = v'\otimes w + v''\otimes w$
• $v\otimes(w' + w'') = v\otimes w' + v\otimes w''$
• $(\lambda v)\otimes w = \lambda\cdot(v\otimes w) = v\otimes(\lambda w)$    (λ ein Element des Grundkörpers K)

Diese Regeln sehen aus wie Distributivgesetze bzw. Assoziativgesetze; auch daher der Name Tensorprodukt.

Ein Kommutativgesetz gilt im Allgemeinen nicht, denn für $v \in V, w \in W$ gehören die Vektoren

$v\otimes w \in V\otimes W$ und $w\otimes v \in W\otimes V$

nur dann demselben Vektorraum an, wenn die Räume V und W identisch sind; und selbst dann muss keine Gleichheit gelten.

Universaldefinition

Bisher wurde die Frage umgangen, welcher Natur denn der mit $V\otimes W$ bezeichnete Vektorraum im allgemeinen Falle ist. Die bisher angegebenen Forderungen an diesen Vektorraum können kondensiert und in mathematischer Sicht unzweideutig in Form einer Universaldefinition angegeben werden.

Als Tensorprodukt der Vektorräume V und W, d.h. als Vektorraum, in welchem die Tensorprodukte von Vektoren aus V und W „leben“, wird jeder Vektorraum X (über dem gemeinsamen Skalarenkörper von V und W) bezeichnet, zu dem es eine bilineare Abbildung $\phi:V\times W\to X$ gibt, die die folgende universelle Eigenschaft erfüllt:

Jede weitere bilineare Abbildung $B:V\times W\to Y$ kann auf eindeutige Weise zu einer linearen Abbildung auf X erweitert werden. Dies heißt exakter, dass es eine eindeutig bestimmte lineare Abbildung $\tilde B:X\to Y$ gibt, so dass für beliebige Paare von Vektoren gilt

$B(v,w)=\tilde B(\phi(v,w))$.

Gibt es einen solchen Vektorraum, so ist er (bis auf Isomorphie) eindeutig. Es wird $X=V \otimes W$ und $\phi(v,w)=v \otimes w$ notiert. Die universelle Eigenschaft kann also als $B(v,w)= \tilde B(v \otimes w)$ geschrieben werden, oft verzichtet man auf die Vergabe unterschiedlicher Bezeichnungen, da der Definitionsbereich aus dem Argument ablesbar ist.

Um nun tatsächlich Vektorräume anzugeben, die diese Definition erfüllen, gibt es zwei übliche Wege. Einmal im endlichdimensionalen Fall über den Raum der Bilinearformen auf den Dualräumen, wie im folgenden angegeben, und zum anderen durch die Konstruktion eines einfach anzugebenden, aber zu großen Raumes, von dem ein Quotientenraum nach einem geeigneten Unterraum die Eigenschaften des Tensorproduktes erhält. Die letztgenannte Konstruktion wird weiter unten im Kontext von Moduln über Ringen ausgeführt.

Tensorprodukt und Bilinearformen

Bilinearformen $V\times W\to K$ entsprechen linearen Abbildungen $V\otimes W\to K$.

Es sei $B: V \times W \to K$ eine Bilinearform. Dann kann man zeigen, dass

$V\otimes W\to K,\qquad v\otimes w\mapsto B(v,w)$

eine wohldefinierte lineare Abbildung ist.

Ist umgekehrt

$\lambda\colon V\otimes W\to K$

eine lineare Abbildung, so ist die Abbildung

$V\times W\to K,\qquad (v,w)\mapsto \lambda(v\otimes w)$

bilinear.

Im Fall endlichdimensionaler Vektorräume kann man das Tensorprodukt von V und W also auch als den Dualraum des Vektorraums aller bilinearen Abbildungen $V\times W\to K$ definieren.

Ein Grund, weshalb man nicht statt des Tensorproduktes mit dem Raum der Bilinearformen arbeitet, ist der folgende: Multilinearformen, also beispielsweise Abbildungen

$U\times V\times W\to K$

für drei K-Vektorräume U, V, W, die linear in jeder Komponente sind, entsprechen linearen Abbildungen

$U\otimes V\otimes W\to K,$

aber es gibt keine ähnlich einfache Möglichkeit, Räume von Multilinearformen durch Räume von Bilinearformen auszudrücken; dabei bezeichnet

$U\otimes V\otimes W$

die Räume

$U\otimes(V\otimes W)$ bzw. $(U\otimes V)\otimes W,$

die mithilfe von

$u\otimes(v\otimes w)=(u\otimes v)\otimes w$

kanonisch identifiziert werden können. Diese Identifizierung entspricht dem Umstand, dass man aus einer Multilinearform

$U \times V\times W\to K$

einerseits durch Festhalten des Argumentes aus U eine Bilinearform

$V\times W\to K,$

andererseits durch Festhalten des Argumentes aus W eine Bilinearform

$U\times V\to K$

erhalten kann.

Erweiterung der Skalare

Ist V ein Vektorraum über K und L ein Erweiterungskörper von K, so kann man das Tensorprodukt

$V_L:=V\otimes_KL$

bilden, indem man auch L als K-Vektorraum auffasst; dies wird durch $\otimes_K$ symbolisiert. V_L wird zu einem Vektorraum über L, wenn man

$\lambda\cdot(v\otimes\mu):=v\otimes(\lambda\mu)\qquad\mathrm{f\ddot ur}\ v\in V,\lambda,\mu\in L$

setzt. Die Dimension von V_L als L-Vektorraum ist gleich der Dimension von V als K-Vektorraum: ist {e_i} eine K-Basis von V, so bildet die Menge

$\{e_i\otimes 1\}$

eine L-Basis von V_L.

Tensorprodukt über einem Ring

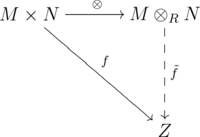
Sei R ein Ring (mit 1, aber nicht notwendigerweise kommutativ). Sei M ein R-Rechtsmodul und N ein R-Linksmodul. Das Tensorprodukt $(M \otimes_R N, \otimes_R)$ über R ist definiert durch eine abelsche Gruppe

$M \otimes_R N$

zusammen mit einer bilinearen Abbildung

$\begin{matrix} \otimes_{R} : & M \times N & \to & M \otimes_{R} N\\ & (x,y) & \mapsto & x \otimes_{R} y, \end{matrix}$

die folgende universelle Eigenschaft erfüllt:

Dass für alle abelschen Gruppen Z und jede bilineare Abbildung

$f: M \times N \to Z\,$

mit

$f(mr,n) = f(m,rn) \qquad (m \in M, r \in R, n \in N)$

ein eindeutig bestimmter Gruppen-Homomorphismus

$\tilde{f}: M \otimes_R N \to Z$

existiert, so dass gilt:

$\tilde{f} \circ \otimes = f.$

Mithilfe der universellen Eigenschaft wird ein bis auf Isomorphie eindeutig bestimmtes Tensorprodukt definiert.

Die Grundkonstruktion

Allerdings ist damit noch nicht die Existenz bewiesen. Diese beweist man, in dem man die abelsche Gruppe $M\otimes_RN$ wie folgt konstruiert:

Man betrachtet den von allen Paaren $(x,y)\in M\times N$ erzeugten freien $\mathbb Z$-Modul $\mathbb{Z}^{(M\times N)}$ und den dazugehörigen Untermodul Q, der durch alle Elemente

• $(m_1 + m_2, n) - (m_1, n) - (m_2, n) \qquad (m_1,m_2\in M; n\in N)$
• $(m,n_1+n_2) - (m, n_1) - (m, n_2) \qquad (m\in M; n_1,n_2\in N)$
• $(mr, n) - (m, rn) \qquad(m\in M; n\in N; r\in R)$

erzeugt wird.

$M\otimes_RN$ ist dann definiert durch den Quotienten von $\mathbb Z^{(M\times N)}$ nach Q, in Zeichen:

$M\otimes_RN:= \mathbb Z^{(M\times N)} / Q$

Spezialfälle

• Ist M ein S-R-Bimodul mit einem weiteren Ring S, so ist

$M\otimes_RN$

ein S-Linksmodul.

• Ist R kommutativ, so ist

$M\otimes_RN$

ein R-Modul; die Moduloperation ist gegeben durch

$r(m\otimes n)=(rm)\otimes n=m\otimes(rn).$

Die Moduln

$M\otimes_RN$ und $N\otimes_RM$

sind kanonisch isomorph.

• Ist A eine R-Algebra, so ist

$A\otimes_RN$

ein A-Linksmodul; die Moduloperation ist gegeben durch

$b(a\otimes n)=(ba)\otimes n$ für a, b in A.

• Ist R ein kommutativer Ring, und sind A und B assoziative R-Algebren, so ist

$A\otimes_RB$

wieder eine assoziative R-Algebra; die Multiplikation ist gegeben durch

$(a_1\otimes b_1)(a_2\otimes b_2) = (a_1a_2) \otimes (b_1b_2).$

Kategorielle Eigenschaften

Verschiedene Varianten des Tensorproduktes besitzen rechtsadjungierte Funktoren:

• Ist R ein Ring, M ein R-Rechtsmodul, N ein R-Linksmodul und P eine abelsche Gruppe, so gilt:

$\mathrm{Hom}_{\mathbf Z}(M\otimes_RN,P)=\mathrm{Hom}_R(M,\mathrm{Hom}_{\mathbf Z}(N,P));$

dabei ist Hom_Z(N,P) ein R-Rechtsmodul via

$(f\cdot r)(n)=f(rn)\quad\mathrm{f\ddot ur}\ f\in\mathrm{Hom}_{\mathbf Z}(N,P), r\in R, n\in N.$

• Ist R ein Ring, S eine R-Algebra, M ein R-Linksmodul und N ein S-Linksmodul, so gilt:

$\mathrm{Hom}_S(S\otimes_RM,N)=\mathrm{Hom}_R(M,N)$.

• Ist R ein kommutativer Ring mit Einselement und M, N, P drei R-Moduln, so gilt:

$\mathrm{Hom}_R(M\otimes_R N,P)=\mathrm{Hom}_R(M,\mathrm{Hom}_R(N,P))$.

Insbesondere ist das Tensorprodukt ein rechtsexakter Funktor.

Das Tensorprodukt ist der Pushout in der Kategorie der kommutativen Ringe mit Einselement; insbesondere ist für einen kommutativen Ring R mit Eins das Tensorprodukt über R das Koprodukt (für endlich viele Objekte) in der Kategorie der R-Algebren.

Beispiele

• Ist R ein Ring, I ein zweiseitiges Ideal und M ein R-Linksmodul, so ist

$M/IM = M\otimes_R R/I.$

• $\mathbb{Z}/n\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/m\mathbb{Z}=\mathbb{Z}/\mathrm{ggT}(m,n)\mathbb{Z}$
• $\mathbb{Q} \otimes_\mathbb{Z} \mathbb{Z}/n\mathbb Z=0$
• Ist R ein kommutativer Ring mit Einselement, so ist

$R[X]\otimes_RR[Y]=R[X,Y].$

• Lokalisierungen von Moduln sind Tensorprodukte mit den lokalisierten Ringen, also ist beispielsweise

$\mathbb{Q}\otimes_{\mathbb{Z}}\mathbb{Q}=\mathbb{Q}.$

Weiterführende Begriffe

In der Differentialgeometrie:

• Tensorfeld
• Differentialform
• Vektorbündel

In der Algebra:

• Flachheit
• Brauergruppe

Literatur

• Siegfried Bosch: Algebra, 7. Auflage 2009, Springer-Verlag, ISBN 3-540-40388-4, doi:10.1007/978-3-540-92812-6, („Tensorprodukt von Vektorräumen“: Abschnitt 4.11 S.230 und „Tensorprodukt über Ringen“: Abschnitt 7.2 S.299)