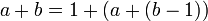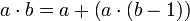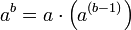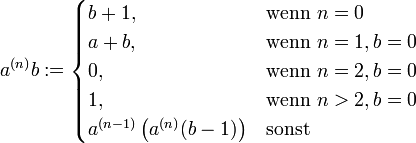- Hyperoperator
-
Der Hyper-Operator ist eine Fortsetzung der herkömmlichen mathematischen Operatoren der Addition, Multiplikation und Potenzierung. Er dient zur kurzen Darstellung großer Zahlen wie Potenztürmen.
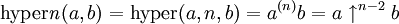
Inhaltsverzeichnis
Herleitung der Notation
Ausgehend von den Beobachtungen
definiert man rekursiv einen dreistelligen Operator (mit
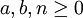 )
)und führt folgende Bezeichnungen ein:
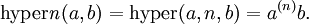 .
.
Somit ist hyper1 die Addition, hyper2 die Multiplikation und hyper3 die Potenzierung. hyper4 wird auch bezeichnet als Tetration oder Superpotenz und kann folgendermaßen notiert werden:
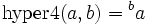 .
.
Allgemeinverständlicher könnte man auch sagen: Schreibe die Zahl a b-mal hintereinander und füge jeweils dazwischen den Operator eine Stufe tiefer ein.
Die Familie wurde für n > 3 nicht für reelle Zahlen erweitert, weil es mehrere „offensichtliche“ Wege dazu gibt, die jedoch nicht assoziativ sind.
Knuths Pfeilnotation
Siehe Hauptartikel: Pfeilschreibweise
Eine andere Schreibweise für den Hyperoperator wurde von Donald Knuth entwickelt, welche als Pfeilnotation bekannt ist. Die Definition ist
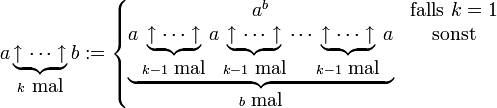
Eine andere Notation verwendet statt des Pfeils
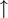 das Zeichen
das Zeichen  . Mit der Definition gilt gerade
. Mit der Definition gilt gerade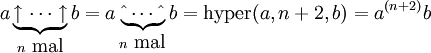 .
.
Diese Notation wird für die Darstellung von sehr großen Zahlen wie etwa Grahams Zahl benutzt.
Eine andere Erweiterung
Es gibt eine andere Möglichkeit, aus den Vorgaben eine allgemeinere Definition der Verknüpfung zu erhalten, denn es gilt auch
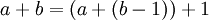
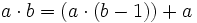
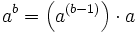 ,
,
weil die Verknüpfungen + und
 kommutativ sind.
kommutativ sind.Daraus ergibt sich die Definition
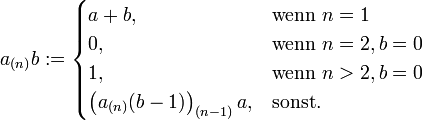
Diese Notation „kollabiert“ jedoch für n = 4; sie ergibt im Gegensatz zu hyper4 keinen Potenz-Turm mehr:
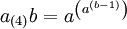
Wie können sich a(n)b and a(n)b plötzlich für n > 3 unterscheiden? Das liegt an der Assoziativität, einer Eigenschaft, die die Operatoren + und
 besitzen (siehe auch Körper), die aber dem Potenz-Operator fehlt. (Im Allgemeinen ist
besitzen (siehe auch Körper), die aber dem Potenz-Operator fehlt. (Im Allgemeinen ist 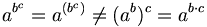 .)
.)Die anderen Ebenen kollabieren nicht auf diese Weise, weshalb auch diese Operatorenfamilie, genannt "niedere hyper-Operatoren" von Interesse ist.
Beispiele
Addition
3(1)3 = 3 + 3 = 6.
Multiplikation
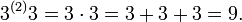
Potenz
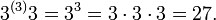
Tetration
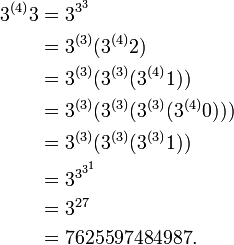
Zu beachten ist hier, dass
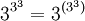 gilt, siehe hierzu auch bei Potenzturm.
gilt, siehe hierzu auch bei Potenzturm.Siehe auch
Weblinks (englisch)
- What Lies Beyond Exponentiation?
- On extending hyper4 to nonintegers
- The Dictionary of Large Numbers (Dictionary's author Robert Munafo claims the (n) notation as his own—it's alright to use it, but it's not a standard.)
- Lynz and the Clarkkkkson
- The Tetration Forum
Wikimedia Foundation.