Kristallklasse — Eine Punktgruppe ist ein spezieller Typus einer Symmetriegruppe der euklidischen Geometrie, der die Symmetrie einer Punktmenge (beispielsweise eines Körpers) beschreibt. Die Punktgruppe einer Symmetriegruppe enthält die so genannten Ableitungen… … Deutsch Wikipedia
LinA — Die Lineare Algebra (auch Vektoralgebra) ist ein Teilgebiet der Mathematik, das sich mit Vektorräumen und linearen Abbildungen zwischen diesen beschäftigt. Dies schließt insbesondere auch die Betrachtung von linearen Gleichungssystemen und… … Deutsch Wikipedia
Lineare Algebra — Die Lineare Algebra (auch Vektoralgebra) ist ein Teilgebiet der Mathematik, das sich mit Vektorräumen und linearen Abbildungen zwischen diesen beschäftigt. Dies schließt insbesondere auch die Betrachtung von linearen Gleichungssystemen und… … Deutsch Wikipedia
Punktgruppen — Eine Punktgruppe ist ein spezieller Typus einer Symmetriegruppe der euklidischen Geometrie, der die Symmetrie einer Punktmenge (beispielsweise eines Körpers) beschreibt. Die Punktgruppe einer Symmetriegruppe enthält die so genannten Ableitungen… … Deutsch Wikipedia
Symmetriepunktgruppe — Eine Punktgruppe ist ein spezieller Typus einer Symmetriegruppe der euklidischen Geometrie, der die Symmetrie einer Punktmenge (beispielsweise eines Körpers) beschreibt. Die Punktgruppe einer Symmetriegruppe enthält die so genannten Ableitungen… … Deutsch Wikipedia
Vektoralgebra — Die Lineare Algebra (auch Vektoralgebra) ist ein Teilgebiet der Mathematik, das sich mit Vektorräumen und linearen Abbildungen zwischen diesen beschäftigt. Dies schließt insbesondere auch die Betrachtung von linearen Gleichungssystemen und… … Deutsch Wikipedia
Adhärenzpunkt — Dies ist ein Glossar einiger Begriffe, die in dem Bereich der Mathematik vorkommen, der als Topologie bekannt ist. Dieses Glossar besteht aus zwei Teilen. Der erste Teil beschäftigt sich mit allgemeinen Konzepten und der zweite Teil erklärt Typen … Deutsch Wikipedia
Basis-Transformation — Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums. Dadurch ändern sich… … Deutsch Wikipedia
Basistransformation — Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums. Dadurch ändern sich… … Deutsch Wikipedia
Basiswechsel (Vektorraum) — Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums über einem Körper K.… … Deutsch Wikipedia
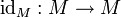 mit
mit 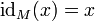 für alle
für alle 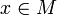 .
.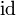 geschrieben. Statt der Notation
geschrieben. Statt der Notation 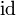 wird manchmal die Schreibweise
wird manchmal die Schreibweise 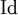 benutzt.
benutzt.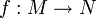 eine beliebige Funktion, dann gilt für die Komposition (Hintereinanderausführung) mit der Identität:
eine beliebige Funktion, dann gilt für die Komposition (Hintereinanderausführung) mit der Identität: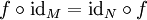 .
.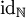 auf der Menge der natürlichen Zahlen ist eine multiplikative Funktion, die in der Zahlentheorie betrachtet wird.
auf der Menge der natürlichen Zahlen ist eine multiplikative Funktion, die in der Zahlentheorie betrachtet wird.