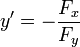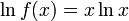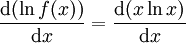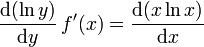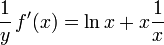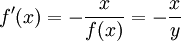- Implizite Ableitung
-
Die Implizite Differentiation (auch implizite Ableitung) ist eine Möglichkeit, eine Funktion, die nicht explizit durch einen Term, sondern nur implizit durch eine Gleichung gegeben ist, mit Hilfe der mehrdimensionalen Differentialrechnung abzuleiten. Sie kann oft auch benutzt werden um die Ableitung von Funktionen, die zwar explizit gegeben sind, in dieser Form aber schwierig abzuleiten sind, zu bestimmen.
Regel
Erfüllt die differenzierbare Funktion
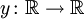 die Gleichung
die Gleichung-
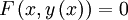 ,
,
wobei auch
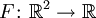 eine differenzierbare Funktion ist, so bedeutet das, dass die Funktion
eine differenzierbare Funktion ist, so bedeutet das, dass die Funktion 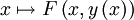 konstant ist. Durch Ableiten mithilfe der Kettenregel erhält man dann
konstant ist. Durch Ableiten mithilfe der Kettenregel erhält man dann-
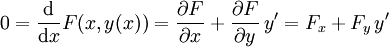 .
.
Hierbei ist
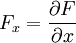 und
und 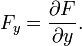
Gilt
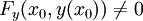 an einer Stelle x0, so gilt dies auch für alle x in einer Umgebung von x0 und man kann die Gleichung nach y' auflösen:
an einer Stelle x0, so gilt dies auch für alle x in einer Umgebung von x0 und man kann die Gleichung nach y' auflösen:Beispiele
1. Die Funktion
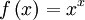 kann mit den herkömmlichen Ableitungsregeln nicht abgeleitet werden, da sowohl Exponent als auch Basis variabel sind. Zunächst kann man durch Logarithmieren den Exponenten eliminieren:
kann mit den herkömmlichen Ableitungsregeln nicht abgeleitet werden, da sowohl Exponent als auch Basis variabel sind. Zunächst kann man durch Logarithmieren den Exponenten eliminieren:Nun leitet man implizit ab, indem man beide Seiten herkömmlich nach x ableitet:
Diese Gleichung kann mit der Kettenregel abgeleitet werden:
Hierbei ist y = f(x). Mit der Regel für die Ableitung des Logarithmus und der Produktregel erhält man:
Löst man nach f'(x) auf und setzt für y wieder f(x) = xx ein , so erhält als Lösung:
-
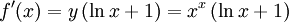 .
.
2. Der Kreis mit Radius r ist gegeben durch die Gleichung x2 + y2 = r2. Teile davon kann man schreiben als Graph einer Funktion y = f(x). Deren Ableitung lässt sich mit Hilfe der impliziten Differentiation wie folgt berechnen:
In die definierende Gleichung setzt man y = f(x) ein:
-
- x2 + f(x)2 = r2
Durch Ableiten dieser Gleichung erhält man
-
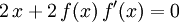 .
.
Auflösen nach f'(x) ergibt:
Daraus folgt zum Beispiel, dass die Tangente an den Kreis im Punkt (x,y) die Steigung
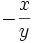 hat.
hat. -
Wikimedia Foundation.