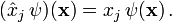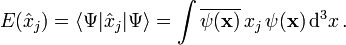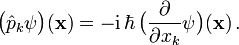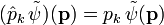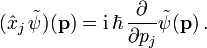- Impulsdarstellung
-
Der Ortsoperator gehört in der Quantenmechanik zur Ortsmessung von Teilchen.
Der physikalische Zustand
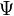 eines Teilchens ist in der Quantenmechanik mathematisch durch einen zugehörigen Vektor eines Hilbertraumes H gegeben. Dieser Zustand wird folglich in der Bra-Ket-Notation durch den Vektor
eines Teilchens ist in der Quantenmechanik mathematisch durch einen zugehörigen Vektor eines Hilbertraumes H gegeben. Dieser Zustand wird folglich in der Bra-Ket-Notation durch den Vektor 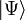 beschrieben. Die Observablen werden durch selbstadjungierte Operatoren auf H dargestellt. Speziell ist der Ortsoperator die Zusammenfassung der drei Observablen
beschrieben. Die Observablen werden durch selbstadjungierte Operatoren auf H dargestellt. Speziell ist der Ortsoperator die Zusammenfassung der drei Observablen 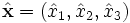 , so dass
, so dassder Mittelwert (Erwartungswert) der Meßergebnisse der j-ten Ortskoordinate des Teilchens im Zustand
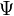 ist.
ist.Definition und Eigenschaften
- Die drei Ortsoperatoren sind selbstadjungierte Operatoren
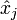 , die mit den ebenfalls selbstadjungierten Impulsoperatoren
, die mit den ebenfalls selbstadjungierten Impulsoperatoren 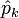 die folgenden, kanonischen Vertauschungsrelationen erfüllen,
die folgenden, kanonischen Vertauschungsrelationen erfüllen,
- Daraus folgt, dass die drei Ortskoordinaten gemeinsam messbar sind und dass ihr Spektrum (Bereich der möglichen Messwerte) aus dem gesamten Raum
 besteht. Die möglichen Orte sind also nicht quantisiert, sondern kontinuierlich.
besteht. Die möglichen Orte sind also nicht quantisiert, sondern kontinuierlich. - Die Ortsdarstellung ist durch die Spektraldarstellung des Ortsoperators definiert. Der Hilbertraum H ist der Raum der quadratintegrierbaren, komplexen Funktionen des Ortsraums
 , jeder Zustand Ψ ist durch eine Ortswellenfunktion
, jeder Zustand Ψ ist durch eine Ortswellenfunktion 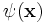 gegeben. Die Ortsoperatoren
gegeben. Die Ortsoperatoren 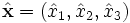 sind die Multiplikationsoperatoren mit den Koordinatenfunktionen, das heißt, der Ortsoperator
sind die Multiplikationsoperatoren mit den Koordinatenfunktionen, das heißt, der Ortsoperator 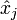 wirkt auf Ortswellenfunktionen ψ(x) durch die Multiplikation der Wellenfunktion mit der Koordinatenfunktion xj
wirkt auf Ortswellenfunktionen ψ(x) durch die Multiplikation der Wellenfunktion mit der Koordinatenfunktion xj
Der Erwartungswert ist
Der Impulsoperator wirkt auf Ortswellenfunktionen (bei geeigneter Wahl der Phasen) als Differentialoperator
- In der Impulsdarstellung wirkt der Impulsoperator multiplikativ auf Impulswellenfunktionen
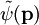
und der Ortsoperator wirkt als Differentialoperator
Wikimedia Foundation.

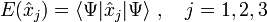
![[\hat{x}_j,\hat{p}_k]=\mathrm i\,\hbar\,\delta_{jk}\ ,\quad
[\hat{x}_j,\hat{x}_k]= 0 = [\hat{p}_j,\hat{p}_k]\ ,\quad j,k\in \{1,2,3\}\,.](/pictures/dewiki/52/43c573379a48f3d056a2a3ee968b8ad8.png)