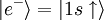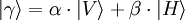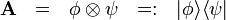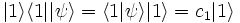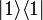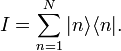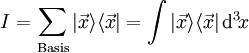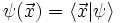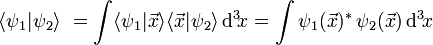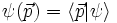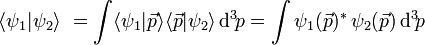Dirac-Schreibweise

Die Kunstwörter Bra und Ket bezeichnen eine spezielle Tensornotation, die insbesondere zur Bezeichnung von Zustandsvektoren in der Quantenmechanik verwendet wird. Der Vorteil dieser Notation besteht darin, dass sie koordinatenfrei ist. Die Gleichungen lassen sich ganz allgemein aufschreiben und man kann später die Koordinaten wählen, die für die Lösung des Problems am besten geeignet sind.

Paul Dirac selbst erfand sowohl die Schreibweise als auch die Benennung, die auf die spitze Klammer (bracket) anspielt, mit der man oft das Skalarprodukt 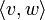$\lang v,w \rang$ zweier Vektoren bezeichnet.

In der Bra-Ket-Notation schreibt man die Vektoren eines Vektorraums V auch außerhalb eines Skalarprodukts mit einer spitzen Klammer als Ket 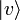$| v \rang$. Jedem Ket 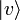$| v \rang$ entspricht ein Bra 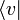$\lang v |$, das dem Dualraum V ^* angehört, also eine lineare Abbildung von V in den zu Grunde liegenden Körper K repräsentiert, und umgekehrt. 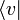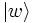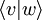Das Ergebnis der Operation eines Bras $\lang v |$ auf einen Ket $| w \rang$ wird $\lang v | w \rang$ geschrieben, womit der Zusammenhang mit der konventionellen Notation des Skalarprodukts hergestellt ist.

Die mathematische Rechtfertigung für die Bra-Ket-Notation ergibt sich aus einem Satz, den F. Riesz und M. Fréchet 1907 unabhängig voneinander bewiesen. Er besagt unter anderem, dass ein Hilbertraum und sein topologischer Dualraum isometrisch isomorph zueinander sind.

Beispiele

Durch die Notation

$|e^{-}\rangle = |1s\uparrow \rangle$

kann ein Elektron im Zustand 1s mit Spin up des Wasserstoffatoms bezeichnet werden.

Der Polarisationszustand eines Photons kann als Überlagerung zweier Basiszustände, z. B. 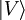$|V\rangle$ (vertikal polarisiert) und 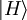$|H\rangle$ (horizontal polarisiert) interpretiert werden:

$|\gamma\rangle = \alpha \cdot |V\rangle + \beta \cdot |H\rangle$

Skalarprodukt

Das Skalarprodukt eines Bra 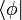$\langle\phi|$ mit einem Ket 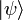$|\psi\rangle$ wird in Bra-Ket Notation geschrieben als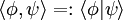

$\langle\phi, \psi\rangle =: \langle\phi| \psi\rangle$

Für beliebige komplexe Zahlen c₁ und c₂ gilt:

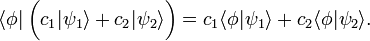$\langle\phi| \; \bigg( c_1|\psi_1\rangle + c_2|\psi_2\rangle \bigg) = c_1\langle\phi|\psi_1\rangle + c_2\langle\phi|\psi_2\rangle.$ (Linearität)

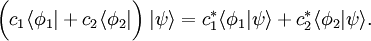$\bigg(c_1 \langle\phi_1| + c_2 \langle\phi_2|\bigg) \; |\psi\rangle = c_1^*\langle\phi_1|\psi\rangle + c_2^*\langle\phi_2|\psi\rangle.$ (Antilinearität)

Aufgrund der Dualitätsbeziehung gilt weiterhin

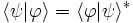$\langle\psi|\varphi\rangle = \langle\varphi|\psi\rangle^*$ (komplexe Konjugation)

Tensorprodukt

Das Tensorprodukt eines Ket 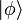$|\phi\rangle$ mit einem Bra 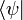$\langle\psi|$ wird geschrieben als

$\bold{A}\ \ = \ \ \phi \otimes \psi \ \ =: \ \ |\phi\rangle\langle\psi|$

Im Fall gewöhnlicher Vektoren entspricht das Tensorprodukt einer Matrix.

Für eine vollständige Orthonormalbasis 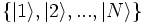$\{|1\rangle,|2\rangle,...,|N\rangle \}$ führt die Operation

$|1\rangle \langle1| |\psi\rangle = \langle1|\psi \rangle |1\rangle = c_1 |1\rangle$

eine Projektion auf den Basiszustand 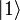$|1 \rangle$ aus. Dies definiert den Projektionsoperator auf den Unterraum des Zustands $|1 \rangle$:

$|1\rangle \langle1|$

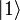Eine besonders wichtige Anwendung der Multiplikation von Ket mit Bra ist der Einheitsoperator I, der sich als Summe über die Projektionsoperatoren ergibt als

$I=\sum_{n=1}^N |n\rangle \langle n|.$

Für eine kontinuierliche Basis ist statt der Summe ein Integral zu bilden. So erhält man beispielsweise für den Ortsraum die Summe über die ganze orthogonale Basis und damit den Einheitsoperator als Integral über den ganzen $\mathbb{R}^3$:

$I= \sum_{\text{Basis}} |\vec{x}\rangle \langle \vec{x}| = \int |\vec{x}\rangle \langle \vec{x}| \, \mathrm{d}^3\! x$

Darstellungen in der Quantenmechanik

In der Quantenmechanik arbeitet man häufig mit Projektionen von Zustandsvektoren auf eine bestimmte Basis anstatt mit den Zustandsvektoren selbst.

Die Projektion auf eine bestimmte Basis wird Darstellung genannt. Ein Vorteil davon ist, dass die so erhaltenen Wellenfunktionen komplexe Zahlen sind, für die der Formalismus der Quantenmechanik als partielle Differentialgleichung geschrieben werden kann.

• Darstellung im Ortsraum (Ortsdarstellung):

Sei 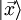$| \vec x \rangle$ ein Eigenzustand des Ortsoperators 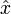$\hat{x}$ mit der Eigenschaft $\hat{x} | \vec x \rangle = \vec x | \vec x \rangle$.

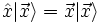Die Wellenfunktion 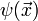$\psi(\vec x)$ ergibt sich durch Projektion als

$\psi(\vec x)=\langle \vec{x}|\psi\rangle$

Das Skalarprodukt im Ortsraum ist

$\langle\psi_1|\psi_2\rangle\ = \int \langle \psi_1 |\vec{x}\rangle\langle \vec{x}|\psi_2\rangle\, \mathrm{d}^3 \! x = \int \psi_1(\vec x)^*\,\psi_2(\vec x)\, \mathrm{d}^3 \! x$

• Darstellung im Impulsraum (Impulsdarstellung):

Sei 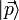$| \vec p \rangle$ ein Eigenzustand des Impulsoperators 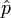$\hat{p}$ mit der Eigenschaft $\hat{p} | \vec p \rangle = \vec p | \vec p \rangle$.

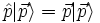Die Wellenfunktion 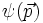$\psi(\vec p)$ ergibt sich durch Projektion als

$\psi(\vec p)=\langle \vec{p}|\psi\rangle$

Das Skalarprodukt im Impulsraum ist

$\langle\psi_1|\psi_2\rangle\ = \int \langle \psi_1 |\vec{p}\rangle\langle \vec{p}|\psi_2\rangle\, \mathrm{d}^3 \! p = \int \psi_1(\vec p)^*\,\psi_2(\vec p)\, \mathrm{d}^3 \! p$

• Erwartungswert des Operators 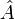$\hat A$ im Ortsraum:

$\langle\psi_1|\hat A|\psi_2\rangle\ = \int \!\!\! \int \langle \psi_1 |\vec{x}\rangle\langle\vec{x}|\hat A|\vec{x}'\rangle\ \langle \vec{x}'|\psi_2\rangle\, \mathrm{d}^3 \! x \, \mathrm{d}^3 \! x' = \int \!\!\! \int \psi_1(\vec x)^* \hat{A}(\vec{x}, \, \vec{x}')\psi_2(\vec{x}')\, \mathrm{d}^3 \! x \, \mathrm{d}^3 \! x'$

Siehe auch

• Quantenzustand
• Erwartungswert
• Quantenchemie
• Liste der Kurzschreibweisen (Physik)