- Intransitive Würfel
-
Intransitive Würfel (die einander gegenüberliegenden Seiten jedes Würfels sind mit der gleichen Zahl beschriftet)Intransitive Würfel nennt man einen Satz spezieller Spielwürfel, in dem es zu jedem der Würfel einen anderen Würfel gibt, gegen den er auf Dauer verliert, das heißt, verglichen mit dem er häufiger eine kleinere als eine größere Zahl zeigt. Ein Beispiel sind die rechts abgebildeten drei intransitiven Würfel A, B und C: Jeweils mit Wahrscheinlichkeit 5/9 gewinnt A gegen B, B gegen C und C gegen A. Das Beispiel der intransitiven Würfel zeigt, dass die Relation „ist mit größerer Wahrscheinlichkeit größer“ für Zufallsvariablen nicht transitiv sein muss. Ein ähnliches Beispiel für eine nichttransitive Relation ist das Spiel Schere, Stein, Papier, in dem jedes Symbol gegen eines gewinnt und gegen ein anderes verliert.
Das Ergebnis des Spiels widerspricht der Intuition, dass ein Vorteil transitiv sein müsse. Diese Vorstellung wäre zutreffend, wenn das Ergebnis die Summe der in einer großen Zahl von Spielrunden gewürfelten Zahlen und nicht die Anzahl der gewonnenen Runden wäre. Einen ähnlichen Irrtum zeigt das Condorcet-Paradoxon.
Inhaltsverzeichnis
Efrons Würfel
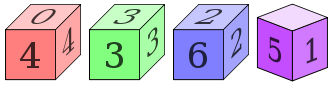
Efrons Würfel sind vier intransitive Würfel, die von dem amerikanischen Statistiker Bradley Efron erfunden wurden.
Die vier Würfel A, B, C und D haben folgende Augenzahlen auf ihren jeweils sechs Seiten:[1]
- A: 4, 4, 4, 4, 0, 0
- B: 3, 3, 3, 3, 3, 3
- C: 6, 6, 2, 2, 2, 2
- D: 5, 5, 5, 1, 1, 1
Für jeden der Würfel gibt es einen anderen, der ihn mit der Wahrscheinlichkeit 2/3 besiegt:
- P(A>B) = P(B>C) = P(C>D) = P(D>A) = 2/3.
Die Wahrscheinlichkeiten für den Vergleich von A mit C und B mit D sind
- P(A>C) = 4/9 und P(B>D) = 1/2.
Miwin’sche Würfel
Miwin'sche Würfel
Die Miwin’schen Würfel wurden 1975 von dem österreichischen Physiker Michael Winkelmann erfunden. Sie sind wie folgt beschriftet:
Satz 1
- III: 1, 2, 5, 6, 7, 9
- IV: 1, 3, 4, 5, 8, 9
- V: 2, 3, 4, 6, 7, 8
Satz 2
- IX: 1, 3, 5, 6, 7, 8
- X: 1, 2, 4, 6, 8, 9
- XI: 2, 3, 4, 5, 7, 9
Gegen jeden der Würfel hat einer der beiden anderen folgende Chancen: Gewinn 17/36, Verlust 16/36 und Unentschieden 3/36.[2]
Literatur
- Hugo Steinhaus, Stanislaw Trybula: On a paradox in applied probabilities, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 7, 1959, S. 67–69 (englisch)
- Martin Gardner: Nontransitive dice and other probability paradoxes, Scientific American 223, Dezember 1970, S. 110–114 (englisch)
- Richard P. Savage: The paradox of nontransitive dice, American Mathematical Monthly 101, No. 5, 1994, S. 429–436 (englisch)
Weblinks
- Ivars Peterson: Tricky Dice Revisited, Science News 161, 15, 13. April 2002 (englisch)
- Jim Loy: Non-Transitive Dice, www.jimloy.com, 2003 (englisch)
- Wolfgang Urban: Nicht-transitive Würfel (PDF-Datei; 129 kB), www.hib-wien.at, September 2009
Einzelnachweise
- ↑ Diese und weitere Möglichkeiten siehe Eric W. Weisstein: Efron’s Dice. In: MathWorld. (englisch)
- ↑ http://unknowns.de/wiki/index.php?title=Miwin'sche_Würfel
Wikimedia Foundation.
