Spielwürfel

Zwei klassische 6-Seiten-Spielwürfel

Verschiedene Spielwürfel mit unterschiedlicher Flächenanzahl

Ein Spielwürfel (meist einfach Würfel genannt) ist ein Gegenstand, der nach einem Wurf auf einer waagerechten Ebene eine von mehreren unterscheidbaren stabilen Ruhelagen einnimmt und in vielen Spielen als Zufallsgenerator dient. Dazu trägt ein Würfel Symbole, von denen eines nach dem Wurf eine ausgezeichnete Lage einnimmt. Dieses Symbol zeigt dann das Ergebnis des Wurfes an.

Der mit Abstand meistverbreitete Spielwürfel ist der mit den Ziffern 1 bis 6 oder entsprechend vielen Punkten, den Augen, beschriftete Kubus oder Hexaeder. Im Alltag ist mit dem Begriff Würfel meist nur dieser Sechsseiter gemeint und so wurde der Name auch für den geometrischen Körper übernommen. Jedoch existieren auch viele andere, im Folgenden ebenfalls beschriebene Würfel. Regelmäßige Benutzer unterschiedlicher Würfeltypen bezeichnen diese häufig mit der Abkürzung W, oder auch d für englisch dice, gefolgt von der Angabe der Seitenanzahl, also beispielsweise W6 oder D6 für einen sechsseitigen, W10, W20, W30 für zehn-, zwanzig- und dreißigseitige Spielwürfel.

Verwendung

Pokerwürfel mit Würfelbecher

Backgammon-Dopplerwürfel

In Würfelspielen sind Würfel das zentrale Spielelement, es zählen nur der Vergleich der Würfelergebnisse selbst oder direkt mit ihnen zusammenhängendes Taktieren. Hier kommen üblicherweise der klassische Sechserwürfel oder speziell bemalte, jedoch immer noch sechsseitige Würfel zum Einsatz. Viele Glücksspiele fallen in diese Kategorie. Bekannte Beispiele im Freizeitbereich sind etwa Kniffel oder Zehntausend, bei denen jeweils bestimmten Augenkombinationen unterschiedlich viele Punkte zugeordnet sind. In Kasinos verbreitet sind unter anderem Craps und Sic Bo, bei denen auf die Ergebnisse einzelner Würfe gewettet wird.

Darüber hinaus sind Würfel in einer Vielzahl von Brettspielen bedeutend, um etwa die Bewegungsgeschwindigkeit von Spielfiguren oder den Ausgang von Zufallsereignissen zu bestimmen. Auch hier kommen in erster Linie Sechsseiter zum Einsatz. Verwendung finden Würfel auch in Rollenspielen, bei denen sich in den letzten Jahrzehnten die Verwendung einer Vielzahl weiterer Würfel mit anderen Seitenzahlen durchgesetzt hat, um die Zufallsentscheidungen flexibler und vielfältiger zu gestalten. Ein eher seltenes, komplett auf Würfel als Spielmaterial setzendes Spielprinzip ist das der Sammelwürfelspiele, bei denen man analog zu Sammelkartenspielen eine Vielzahl von Würfeln käuflich erwerben und taktisch einsetzen muss. Der bekannteste Vertreter ist Dragon Dice.

In allen diesen Bereichen gibt es neben dem einfachen Wurf eines Würfels auch Gelegenheiten, bei denen mehrere Würfel gleichzeitig zu werfen sind. Dabei können die Ergebnisse addiert werden (eine Waffe in einem Rollenspiel richtet soviel Schaden an, wie zwei Würfel zusammen anzeigen) oder als Ensemble betrachtet werden (bei vielen Brettspielen folgen besondere Aktionen, wenn mehrere Würfel die gleiche Zahl zeigen, bei einem sogenannten Pasch). Um das Werfen mehrerer Würfel zu vereinfachen, Schummeln durch Trickwürfe zu vermeiden oder das Ergebnis vor anderen Spielern zu verbergen, kommen Würfelbecher (auch Knobelbecher genannt) zum Einsatz. Hochwertige Exemplare besitzen innen sogenannte Lippen, damit die Würfel beim Herausrollen in jedem Fall springen. Dies soll das Wurfergebnis unabhängig von der ursprünglichen Lage der Würfel machen. Dem gleichen Zweck dient der Würfelturm. Um laute Aufprallgeräusche und ein Wegrollen der Würfel zu vermeiden, wird manchmal auch ein gepolstertes und berandetes Brett (Würfelbrett oder Würfelteller genannt) eingesetzt.

Statt mit ihnen zu würfeln, also Zufallsergebnisse zu erzeugen, können Würfel auch gezielt auf bestimmte Werte gedreht und so zu deren Anzeige genutzt werden. Bekanntestes Beispiel sind die Dopplerwürfel, mit denen im Backgammon die Wertung einer Partie dargestellt wird. Würfel werden auch beim Geschicklichkeitsspiel Dice Stacking verwendet.

Allgemeine Eigenschaften

Standardwürfel in Unicode

Codepoint	Zeichen (200%)	Bezeichnung
U+2680	⚀	DIE FACE-1
U+2681	⚁	DIE FACE-2
U+2682	⚂	DIE FACE-3
U+2683	⚃	DIE FACE-4
U+2684	⚄	DIE FACE-5
U+2685	⚅	DIE FACE-6

Siebenseitiger Würfel: Beispiel für verschiedene Seitentypen und nur annähernde Idealität

Transparente Präzisionswürfel

Als Zufallsgenerator eingesetzt, wird von einem Würfel üblicherweise eine Gleichverteilung der möglichen Ergebnisse erwartet. Diese sollen also auf lange Sicht gleich häufig eintreten, falls die Würfe nicht bewusst beeinflusst werden. Dann nennt man den Würfel einen fairen, idealen oder echten Würfel oder – nach Pierre-Simon Laplace, der an der Gleichverteilung forschte – einen Laplace-Würfel. Bei der Fertigung des Würfels treten immer Abweichungen auf (siehe Herstellung), durch die der Würfel nicht ganz ideal ist. Für hochwertige Würfel kann man diese aber sehr gering halten.

Wenn man von diesen Abweichungen absieht, dann ist Idealität eine Eigenschaft des Bauplans des Würfels, also unter anderem seiner geometrischen Form. Der Bauplan ist genau dann ideal, wenn die Ruhepositionen des Würfels aufgrund seiner Symmetrie erst durch eine Beschriftung unterscheidbar werden. Ein Würfel wird meistens nach einem konvexen Polyeder gestaltet. Ein solches ist genau dann ideal, wenn seine Flächen alle die gleiche Form und Größe haben, und wenn man zwei Flächen nicht anhand ihrer relativen Position zu den anderen Flächen unterscheiden kann. Diese Bedingung erfüllen nur die fünf platonischen Körper, die catalanischen Körper, und gewisse Verzerrte dieser beiden Klassen, sowie Spindeln und Walzen. Nebenbei werden diese Formen wegen ihrer Symmetrie auch als besonders ästhetisch empfunden.

Andere Polyeder haben verschiedene Typen möglicher Landeflächen, wodurch sich deren Landewahrscheinlichkeiten unterscheiden können. Bei einigen Formen kann man versuchen, dies durch die richtige Wahl der Größenverhältnisse auszugleichen, etwa durch Streckung der Seitenflächen beim nebenstehenden Prisma als siebenseitiger Würfel. Allerdings können die Landewahrscheinlichkeiten neben der Geometrie noch von anderen Bedingungen abhängen, zum Beispiel von der Reibung zwischen Würfel und Unterlage oder – auch unbeabsichtigt – von der Wurftechnik. Wenn man diese Bedingungen nicht vorab kennt oder wenn sie wechseln, dann ist ein genauer Ausgleich von vornherein unmöglich. Würfel, die auf solchen Körpern beruhen, können deshalb nie wirklich ideal sein.

Weitere Anforderungen sind, dass der Würfel gut - aber nicht zu lange - rollt, und dass die Ruhelagen eine gewisse Stabilität aufweisen. Hierdurch wird die Formgebung weiter eingeschränkt; so sind etwa Würfel mit einer hohen Zahl von Ruhelagen schwerer zu konstruieren. Oft werden auch die Ecken und Kanten abgerundet, um Rollverhalten und Handhabung zu verbessern. Beim Casinospiel Craps sowie von einigen Rollenspielern ist dies jedoch verpönt, da ungleichmäßige Abrundungen bestimmte Landeflächen bevorzugen könnten.

Gelegentlich wird die Wahrscheinlichkeitsverteilung auch bewusst zugunsten bestimmter Ergebnisse manipuliert, möglichst ohne den Würfel optisch zu verändern, um sich im Spiel einen Vorteil zu verschaffen. In diesem Fall nennt man den Würfel gezinkt. Die Möglichkeiten beinhalten das Verändern der Gewichtsverteilung, unterschiedlich stark abgerundete Kanten oder Ecken sowie verzogene Flächen. Zu stark gezinkte Würfel verraten sich durch eine torkelnde Rollbewegung, was beim Einsatz eines Würfelbechers aber nicht auffällt. Eine weitere Möglichkeit ist es, im Inneren des Würfels einen Dauermagneten zu platzieren, um den Würfelwurf bei Bedarf durch einen zweiten Magneten, den man z. B. unter die Tischplatte hält, zu beeinflussen. Um das Zinken zu erschweren, werden in Kasinos oft transparente Würfel eingesetzt.

Geschichte

Altertum

Steinerner Astragal

Würfel aus mittelprotoattischer Zeit (um 680 v. Chr.) des Malers der Widder-Kanne, Archäologisches Nationalmuseum Athen

Asiatische historische Spielwürfel

Die ältesten bekannten Würfel gehören zu einem altiranischen Brettspiel, das auf 3000 v. Chr. datiert wird und einen möglichen Vorläufer des Backgammon-Spiels darstellt ^[1]. Weitere frühe Funde stammen aus Tepe Gawra (nördlicher Irak), frühes 3. Jahrtausend v. Chr., und Mohenjo-Daro (Pakistan), spätes 3. Jahrtausend v. Chr ^[2]. Diese Funde haben bereits die Form eines Kubus und sind mit Augen gekennzeichnet. Auch aus der weiteren Frühgeschichte und Antike des Orients sind zahlreiche sechsseitige Würfel erhalten.

Daneben stammt aus der sumerischen Stadt Ur ein auf ca. 2600 v. Chr. datiertes Spiel. Darin wurden Würfel für die Bestimmung der Bewegungsweite eingesetzt. Eine Partei verwendete vierseitige Stäbe, die andere Tetraeder, die an zwei Ecken markiert waren. Dies sind die ältesten bekannten Würfel in Form eines anderen regulären Polyeders als des Kubus. ^[3]

Im ägyptischen Spiel Senet wurden mehrere halbrunde Holzstäbchen verwendet, die auf einer Seite markiert waren und so durch ihre Lage nach dem Werfen abgelesen werden konnten. Der erste sichere Fund zu Senet ist ein Grabgemälde, das auf 2686 v. Chr. datiert wird. Es gibt aber auch Spielbrettfunde, die bis 3500 v. Chr. zurückgehen und vermutlich ebenfalls zu Senet gehören. Somit ist auch dieses Spiel ein Kandidat für den ersten Einsatz würfelartiger Gegenstände.^[4] Außerdem wurden in Ägypten auch Sprunggelenkknöchelchen von Paarhufern wie Schafen oder Ziegen als Würfel verwendet.

In der griechischen und römischen Kultur dienten diese Knöchelchen, Astragali genannt, unter anderem zu Orakelzwecken. Durch ihre kantige Form haben sie vier verschiedene mögliche Ruhepositionen, die Wahrscheinlichkeit für die Ergebnisse ist unterschiedlich hoch. Daneben wurden auch Würfel moderner Form verwendet. Schon antike Autoren hatten Theorien zu ihrer Erfindung, unter anderem schrieb Plinius der Ältere sie Palamedes während des Trojanischen Krieges zu und Herodot dem Volk der Lyder ^[5]. Es ist jedoch davon auszugehen, dass sie aus dem Orient übernommen wurden. Dabei waren neben sechsseitigen auch bereits Würfel mit höheren Seitenzahlen bekannt, unter anderem gibt es Funde von 12-, 18-, 20- und 24-seitigen Würfeln ^[6]. An Materialien ist ein weites Spektrum überliefert, unter anderem Ton, Metall, Elfenbein, Kristall, Knochen und Glas. Auch gab es bereits Würfel mit Buchstaben und Wörtern statt Zahlen oder Augen, die für die Wahrsagerei oder komplexe Würfelspiele benutzt wurden.

Sowohl Würfel als auch Astragali wurden neben der Wahrsagerei auch für Würfelspiele verwendet. Dabei existierten Spiele für Kinder und Frauen, die teils eher Geschicklichkeits-Wurfspiele, teils Würfelspiele im modernen Sinn waren. Das bekannteste Beispiel ist Astragaloi. Würfel und Astragali darüber hinaus für Glücksspiele um Geld zu verwenden, war im Römischen Reich außerhalb der Saturnalien verboten und galt als schweres Laster, war jedoch dennoch weit verbreitet ^[7].

Eine weitere unabhängige Entstehung von Spielwürfeln gab es in Indien. Hier existierten seit der Vedischen Zeit rituelle und Gesellschaftsspiele, bei denen die Nüsse des Vibhidaka-Baumes (Terminalia bellerica) als fünfseitiger Würfel verwendet wurden. Später (im Spiel Jataka) entwickelten sich vierseitige Prismenwürfel (s. u.). ^[8] Des Weiteren ist davon auszugehen, dass die dem Würfeln verwandte Zufallsentscheidung des Münzwurfes wohl seit der Erfindung der Münze an sich betrieben wird. Münzen lassen sich als zweiseitige Würfel auffassen (s. u.), was somit ebenfalls eine Form mit langer Geschichte ist.

Mittelalter und frühe Neuzeit

Backgammon-Würfel vom 1628 gesunkenen Kriegsschiff Vasa

Durch römische Legionäre und Kolonisten wurden Würfel und Würfelspiele ins restliche Europa gebracht. Im Mittelalter waren die Knöchel noch unter dem Namen Buckelhörner bekannt, allmählich setzten sich aber ausschließlich die modernen, regelmäßig geformten Würfel durch. Wie in der Antike war der sechsseitige Würfel eindeutig dominierend, aber weiterhin tauchten auch vereinzelt andere Seitenzahlen auf: 965 entwarf der französische Kleriker Wibold ein Spiel, das einen vierseitigen Prismenwürfel verwendete, und auch ein mittelalterliches achtseitiges Prisma ist bekannt ^[9].

Die Würfel der Wikinger waren aus Fischbein, Geweih, Knochen oder Pechkohle. Oft waren sie rechteckig, die 1 und 2 an den Enden und die 3, 4, 5, 6 auf den vier langen Seiten. Die Summe der beiden gegenüberliegenden Seiten betrug meistens nicht 7. Ein skurriler Würfel stammt aus Dublin. Er hat die Form der heutigen Würfel, war jedoch nur mit den Zahlen 3, 4, 4, 5, 5, 6. versehen.

Würfelspiele verschiedenster Ausprägungen waren in allen Ländern Europas und bei allen Schichten beliebt, sie werden in zahlreichen zeitgenössischen Werken erwähnt. Schon früh gab es auch professionelle Glücksspieler ^[10], 1254 werden in einer Verordnung Ludwigs IX. erstmals spezielle Spielhäuser erwähnt ^[11]. Auch über gezinkte Würfel gibt es vielfältige Berichte ^[12].Trotz der großen gesellschaftlichen Verbreitung galten Glücksspiele mit Würfeln weiterhin als Laster und es wurde mit weltlichen wie kirchlichen Verboten gegen sie vorgegangen. In der französischen Literatur wurde der Würfel teils als Erfindung des Teufels gebrandmarkt ^[13].

Moderne

Waren Würfel in der Vergangenheit hauptsächlich für reine Würfelspiele und nur selten wie beim Backgammon als Teile anderer Spielarten verwendet worden, kamen sie im Verlauf des 20. Jahrhunderts in einer wachsenden Zahl von Gesellschaftsspielen zum Einsatz. Auf dem Massenmarkt beschränkte sich dies fast immer auf sechsseitige Würfel. Andere Formen tauchten erstmals mit dem Aufschwung der Tabletop-Spiele in den 1960er Jahren im größeren Stil auf. Das erste erfolgreiche Pen-and-Paper-Rollenspiel Dungeons & Dragons etablierte dann ab 1974 die fünf platonischen Körper plus den zehnseitigen Würfel als weitverbreitete Modelle. Durch die wachsende Vielzahl der Rollenspielsysteme und beginnendes Sammlertum entstand in den folgenden Jahrzehnten ein Bedarf an immer exotischeren Würfeln und Firmen, die diesen decken, wurden gegründet.

Herstellung

Produktionsspur an einem Gamescience-Würfel

Craps-Präzisionswürfel, matt und mit scharfen Kanten (razor edge)

Die meisten Würfel bestehen heute aus Kunststoff (ABS), recht verbreitet ist auch noch Holz, gelegentlich werden auch weitere Materialien wie Kork, Horn, Stein, Metall oder Karton verwendet. Der Standardwürfel hat einen Durchmesser von etwa eineinhalb Zentimetern, aber der Markt deckt ein breites Größenspektrum ab. Plastikwürfel werden üblicherweise gegossen, wobei ein Einfüllpropfen übrigbleibt, der zusammen mit anderen Unebenheiten durch maschinelles Abrollen geglättet wird. Die Beschriftungen sind meist Vertiefungen, in die dann Farbe eingefüllt wird, seltener aufgedruckt. Genaugenommen stellen diese verschiedenen Bearbeitungen der Seiten ein leichtes Zinken dar, der Effekt ist aber minimal und in der Praxis vernachlässigbar.

Für den Würfel- und Brettspielmassenmarkt gibt es eine Vielzahl an Produzenten, für die exotischeren Rollenspielwürfel existiert jedoch weltweit nur eine kleine Anzahl renommierter Hersteller. Viele der im Folgenden genannten Würfelsorten werden auch ausschließlich von einer dieser Firmen hergestellt, da manche Konstruktionen wie das Zocchihedron sogar patentiert sind. Unter diesen Firmen beherrschen vor allem Koplow und Chessex Games den Massenmarkt, GameScience und Crystal Caste haben sich auf exklusivere Modelle spezialisiert und setzen sich auch teils in den Herstellungsverfahren ab; so lehnt etwa GameScience das Abrollen der Produktionsspuren ab, da dies der Idealität des Würfels stärker schaden soll als die Spuren selbst ^[14].

Besonders aufwendig ist auch die Herstellung von Kasino-Würfeln, auch Präzisionswürfel genannt. Für das professionelle Glücksspiel werden höchste Anforderungen an die Idealität der verwendeten Würfel gestellt. Dazu wird statt der üblichen Kunststoffe Celluloseacetat verwendet, das sich komplett blasenfrei herstellen und somit besonders exakt verarbeiten lässt. Die Würfel werden nicht gegossen, sondern früher mit Diamanten, heute mit Lasern aus größeren Blöcken geschnitten. Seit den 1960ern ersetzt Celluloseacetat das leicht brenn- und lösbare Cellulosenitrat. Aber auch das modernere Material hat eine Schwäche: es ist temperatur-, feuchtigkeits- und lichtempfindlich und beginnt nach einiger Zeit zu kristallisieren und spröde zu werden  ^[15]. Neben den höheren Kosten ist dies ein Grund, weshalb derartige Würfel nur in Kasinos zum Einsatz kommen, wo sie häufig ausgetauscht werden, und nicht im Privateinsatz, bei dem die Nutzungsdauer meist wesentlich länger ist. Die Toleranzen für die Form von Kasinowürfeln liegen im Bereich von 0,0005 ^[16] oder 0,0002 ^[17] Zoll (0,0127 bzw. 0,00508 mm).

Um die Ausgeglichenheit der Würfelergebnisse nicht zu gefährden, wird bei Kasinowürfeln außerdem zur Füllung der Augen nur Farbe mit der Dichte des Würfelmaterials verwendet. Je nach Spiel und Kasino sind die Kanten und Ecken scharf (razor edge) oder abgerundet (ball cornered) und die Oberfläche matt (sanded) oder poliert (polished). Bei letzterer Behandlung sind die Würfel durchsichtig, wodurch einige Zinkmethoden (s. o.) erkennbar würden. Zu den verwendeten Sicherheitsmerkmalen gehören außerdem Seriennummern, im Inneren sichtbare Zeichen oder auf UV-Licht reagierende Beschichtungen ^[18].

Formen

Das wichtigste Unterscheidungskriterium von Würfeln ist die Anzahl ihrer Seiten und damit der Zahlenbereich, aus dem sie Zahlen generieren können. Gemäß der bei Rollenspielern üblichen Terminologie werden im Folgenden die Würfel entsprechend der Anzahl n ihrer Seiten als Wn bezeichnet, der normale sechsseitige Würfel also als W6. Verbreitet ist auch die Bezeichnung dn von englisch dice. Die Spalte Ideal gibt an, ob bei einem perfekt gefertigten Vertreter einer Form alle Ergebnisse mit der gleichen Wahrscheinlichkeit einträten (siehe oben).

Die Standard-Würfel

Die folgenden sechs Würfel haben sich unter dem Einfluss von Dungeons & Dragons als Standard-Sortiment unter Rollenspielern herausgebildet und sind dadurch die mit Abstand meistverbreiteten Würfeltypen. Es sind die fünf platonischen Körper und ein Trapezoeder. Alle sechs sind aufgrund ihrer symmetrischen Form ideal.

Typ			Form	Ideal	Weitere Informationen
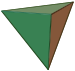
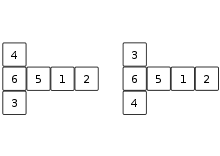
W4			Tetraeder	Ja	Platonischer Körper aus vier gleichseitigen Dreiecken. Beim W4 bleibt stets eine Spitze oben liegen, so dass das normale Ableseverfahren nicht umsetzbar ist. Es existieren zwei Varianten des W4: Bei beiden stehen auf jeder Fläche drei Zahlen, die so angeordnet sind, dass der Würfel aus jedem Blickwinkel das gleiche Ergebnis zeigt. Diese befinden sich entweder an den Kanten oder den Ecken. Bei der Kantenvariante zählt als Würfelergebnis die an den Kanten mit Bodenkontakt angezeigte Zahl, bei der Eckenvariante die Zahl an der obenliegenden Ecke. Da der W4 sehr schlecht rollt, wird er gewöhnlich hochgeworfen wie bei einem Münzwurf.
W6			Hexaeder	Ja	Platonischer Körper aus sechs Quadraten. Der W6 ist der in nahezu allen Alltagsspielen vorkommende Würfeltyp und wird somit oft als der Spielwürfel betrachtet. Die Summe der gegenüberliegenden Seiten ist in Standardbeschriftung stets 7.
W8			Oktaeder	Ja	Platonischer Körper aus acht gleichseitigen Dreiecken. In Standardbeschriftung ist die Summe der gegenüberliegenden Seiten 9.
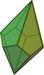
W10			pentagonales Trapezoeder	Ja	Körper aus zehn Drachenvierecken (als einziger der gängigen Würfel kein platonischer Körper). Üblicherweise wird er mit den Zahlen 0–9 beschriftet, wobei die 0 dann oft als 10 gewertet wird. Ohne diese Umwertung ist die Summe gegenüberliegender Seiten 9. Es gibt selten Versionen mit den Zahlen 1-10, in dem Fall ergeben die gegenüberliegenden Seiten die Summe 11. Mit anderer Beschriftung wird dieser Würfel auch als Zehnerstellenwürfel beim W100 genutzt (s. u.).
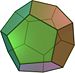
W12			Dodekaeder	Ja	Platonischer Körper aus zwölf regelmäßigen Fünfecken. In Standardbeschriftung ist die Summe der gegenüberliegenden Seiten 13.
W20			Ikosaeder	Ja	Platonischer Körper aus 20 gleichseitigen Dreiecken. In Standardbeschriftung ist die Summe der gegenüberliegenden Seiten 21. Durch die doppelte Vergabe der Zahlen 0-9 entsteht ein „platonischer W10“.

Sonstige Polyeder

Diese Würfel haben die Form eines stark symmetrischen, aber nicht platonischen Polyeders. Catalanische oder archimedische Körper eignen sich hierfür besonders gut, wobei die Catalanischen Körper aufgrund ihrer identischen Flächen als ideal gelten, was auf die Archimedischen Körper nicht zutrifft.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W12	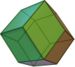		Rhombendodekaeder	Ja		Catalanischer Körper aus 12 identischen Rhomben (Rauten).
W14			Kuboktaeder	Nein		Archimedischer Körper aus 6 Vier- und 8 Dreiecken.
W24			Tetrakishexaeder	Ja	Chessex, GameScience, Koplow	Catalanischer Körper aus 24 gleichschenkligen Dreiecken. Man kann sich das Gebilde als Kubus mit auf allen Seiten aufgepfropften vierseitigen Pyramiden vorstellen. In Standardbeschriftung ist die Summe der gegenüberliegenden Seiten 25.
W24			Deltoidalikositetraeder	Ja		Catalanischer Körper aus 24 identischen Deltoiden.
W26			Kleines Rhombenkuboktaeder	Nein		Archimedischer Körper aus 8 Dreiecken und 18 Quadraten.
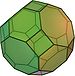
W26			Großes Rhombenkuboktaeder	Nein		Archimedischer Körper aus 12 Quadraten, 8 Sechsecken und 6 Achtecken.
W30			Rhombentriakontaeder	Ja	GameScience, Koplow	Catalanischer Körper aus 30 identischen Rhomben. In Standardbeschriftung ist die Summe der gegenüberliegenden Seiten 31.
W32			Ikosidodekaeder	Nein		Archimedischer Körper aus 12 Fünfecken und 20 gleichseitigen Dreiecken.
W32			Ikosaederstumpf	Nein		Archimedischer Körper aus 12 Fünfecken und 20 gleichseitigen Sechsecken.
W48			Hexakisoktaeder	Ja		Catalanischer Körper aus 48 identischen Dreiecken.

Prismen

Prismen- oder Säulenwürfel bestehen aus zwei Grundflächen und einer beliebigen, meist relativ kleinen ungeraden Anzahl von Seitenflächen. Fällt ein Prismawürfel ungerader Flächenanzahl auf eine seiner Seitenflächen, so weist eine Kante nach oben. Deshalb werden hier die Werte mit über die Seitenkanten verlaufenden, farbig abgegrenzten Punkten angezeigt. Alternativ erfolgt die Beschriftung wie bei einem herkömmlichen W4, da in den möglichen Ruhepositionen keine der Seitenflächen oben liegt.

Prismawürfel mit mehr als zwei Flächen sind nur schwer als ideale Würfel herstellbar, da die korrekten Verhältnisse von Seiten- und Grundflächen für eine ausgeglichene Wahrscheinlichkeitsverteilung schwer zu berechnen sind. GameScience sind aber zumindest angeblich ideale W5 und W7 gelungen – gemeinhin werden derartige Formen aber als nicht ideal angesehen.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W2			Zylinder (Scheibe)	Ja		Ein W2 ist meist kein eigentlicher Würfel, sondern eine simple Münze, die gemäß dem üblichen Benennungsschema scherzhaft so genannt wird. Neben Alltagssituationen sind 50-50-Zufallsentscheidungen auch in vielen Spielen erforderlich, sodass manche Würfelhersteller zur Vervollständigung ihres Sortimentes auch speziell beschriftete Scheiben produzieren. Der Rand des W2 stellt die einzige Seitenfläche dar und wird aufgrund seiner äußerst geringen Trefferwahrscheinlichkeit im Normalfall vernachlässigt.
W3			Dreiecksprisma	(Ja)	Diverse (für spezielle Brettspiele)	Diese Form eines W3 verfügt über zwei unbeschriftete Deckflächen mit einer nicht verschwindenden Landewahrscheinlichkeit. Wird bei einem solchen Ergebnis der Wurf wiederholt, ist der Würfel hinsichtlich der Endergebnisse noch ideal. Eine Walzenform (s. u.) umgeht diese Schwäche.
W5			Dreiecksprisma	Nein	GameScience	Ein W5 ist eine Dreieckssäule, deren Deckflächen mit 1 und 5 beschriftet sind. Die Werte 2–4 sind auf die Seitenflächen verteilt und an den schmalen Kanten markiert. Der bekannte W5 von GameScience ist genaugenommen kein echter Prismenwürfel, der Übergang von Seiten- zu Deckflächen wurde für besseres Verhalten abgeschrägt.
W7			Fünfecksprisma	Nein	GameScience	Der W7 ist eine Fünfeckssäule, deren Deckflächen mit 1 und 7 beschriftet sind. Die Werte 2–6 sind auf die Seitenflächen verteilt und an den Kanten markiert.
W9			Siebenecksprisma	Nein	GameScience	Der W9 ist eine Siebeneckssäule, deren Deckflächen mit 1 und 9 beschriftet sind. Die Werte 2–8 sind auf die Seitenflächen verteilt und an den Kanten markiert. Da derartige Würfel selten sind, wird als Abhilfe üblicherweise ein W10 verwendet; bei einem 0-Wurf wird erneut geworfen.

Walzen

Für Walzenwürfel gibt es zwei verschiedene, aber ähnliche Konstruktionsweisen: Zum einen können n-seitige Prismen verwendet werden, denen an den Deckflächen entsprechend n-seitige Pyramiden aufgesetzt werden. Die andere Möglichkeit sind Antiprismen (also wechselseitig versetzte Dreiecke als Seitenflächen) mit $\frac{n}{2}$-seitigen Pyramiden auf den Deckflächen. In beiden Fällen sorgen die Pyramiden dafür, dass weder die Deckflächen noch die Pyramidenflächen als Ergebnis auftreten können, die Werte verteilen sich also ausschließlich über die Seitenflächen. Das Prisma-Prinzip ermöglicht jede Seitenanzahl $\ge 3$, wird aber eher selten verwendet. Bei ungerader Zahl der Seitenflächen tritt das Problem auf, dass es nach einem Wurf keine obenliegende Seite gibt, dies kann durch Kantenbeschriftung wie bei Prismen gelöst werden. Bei der Antiprisma-Variante sind ausschließlich gerade Seitenanzahlen $\ge 4$ möglich, sie ist die stärker verbreitete Form der Walzenwürfel, meist als Alternative zu den Standardwürfeln. Mit vier Seiten ergibt sich ein Tetraeder, und die Deckflächen degenerieren zu Linien, so dass die aufgesetzten Pyramiden entfallen.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W3			Dreiecksprisma mit aufgesetzten Pyramiden	Ja		In dieser Form gut möglich, aber kaum anzutreffen.
W4			Quadratprisma mit aufgesetzten Pyramiden	Ja	Diverse
W4			Verzerrtes Tetraeder	Ja		Dieser W4 stellt eine entartete Sonderform der Antiprisma-Walzen-Konstruktion dar: er besteht zwar aus Dreiecken, die um jeweils 180° versetzt angeordnet sind, besitzt aber statt der aufgesetzten Pyramiden lediglich zwei Kanten.
W6			Dreiecksantiprisma mit aufgesetzten Pyramiden	Ja	Diverse
W7			Abgerundetes Siebenecksprisma	Ja		In der abgebildeten Form Abrundungen statt Pyramiden, dies ist allgemein eine Alternative.
W8			Quadratantiprisma mit aufgesetzten Pyramiden	Ja	Diverse
W10			Fünfecksantiprisma mit aufgesetzten Pyramiden	Ja	Diverse	Die Anordnung der Flächen entspricht dem Ikosaeder (W20), allerdings ist der Mittelteil gestreckt.
W12			Sechsecksantiprisma mit aufgesetzten Pyramiden	Ja	Diverse
W12			Zwölfecksprisma mit aufgesetzter Pyramide	Ja		Diesem Modell ist nur an einer Seite eine Pyramide aufgesetzt, sodass es eher gekreiselt als gewürfelt werden muss.
W20			Zehnecksantiprisma mit aufgesetzten Pyramiden	Ja	Diverse

Spindeln

Es gibt zwei Klassen von geometrischen Körpern, die optisch Spindeln oder Kreiseln ähneln. Dies sind zum einen die Bipyramiden, die aus zwei mit der Grundfläche zusammengeklebten Pyramiden bestehen, sodass am „Äquator“ jeweils zwei Flächen aufeinandertreffen. Soll die Beschriftung auf den Flächen erfolgen, muss jede der beiden Pyramiden eine gerade Seitenzahl haben, damit eine Fläche oben liegen kann. Damit sind nur Würfel mit 4n Seiten möglich, anders ausgedrückt: jeder Halbkörper muss eine geradzahlige Flächenzahl haben, da sonst eine Kante oben liegen würde. Die andere Sorte sind Trapezoeder, die aus Drachenvierecken bestehen. Diese sind so angeordnet, dass am „Äquator“ jeweils Fläche und Kante aufeinanderstoßen, dieser erhält dadurch einen Zickzack-Verlauf. Für Flächenbeschriftung sind hier - aus demselben Grund wie oben - nur Seitenzahlen 4n+2 möglich.

Durch Kantenbeschriftung sind auch die jeweils anderen Seitenzahlen möglich, also Bipyramiden mit 2n Seiten, n ungerade, und Trapezoeder mit 2n Seiten, n gerade. In der Praxis werden jedoch nur die Flächenbeschriftungen verwendet. Die Hälften beider Formen wirken bei hohen Seitenzahlen wie angeschnittene Kegel. Neben den unten aufgeführten exotischeren Würfeln gehören auch zwei der Standardwürfel zu dieser Klasse: der W8 ist eine Bipyramide, der W10 ein Trapezoeder. Auch der W6 kann als Trapezoeder aufgefasst werden.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W14			14-seitiges Trapezoeder	Ja	Chessex, GameScience	In dieser Version zusätzlich zweimal mit den Wochentagen beschriftet.
W16			16-seitige Bipyramide	Ja	Chessex, GameScience
W34			34-seitiges Trapezoeder	Ja	Chessex	Der W34 wird als Danish Lottery Die vermarktet und soll tatsächlich in der dänischen Lotterie als Zufallsgenerator verwendet worden sein.
W48			48-seitige Bipyramide	Ja
W50			50-seitiges Trapezoeder	Ja	GameScience

Kugeln

Kugelwürfel sind eine sehr ungewöhnliche Konstruktionsweise. Auch gerade deshalb gilt einer von ihnen, der Zocchihedron-W100, als eine Art Krönung der Rollenspiel- oder allgemein exotischen Würfel.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W6			Kugel	Ja	Diverse	Im Inneren befindet sich ein Hohlraum mit Hexaeder-förmigen Skelett und einer Kugel, die in einer der sechs Mulden zum Liegen kommt. Die Kugel hat damit sechs stabile Zustände. Dieser W6 ist ebenso ideal wie ein normaler Kubus. Je nach Produktionsqualität kann es bei dieser Form zu sehr langen Rolldauern kommen.
W32			Kugel	Nein		Eine Kugel mit 32 Vertiefungen.
W50			Kugel	Nein		Eine Kugel mit 50 Vertiefungen.
W100			Kugel	Nein	GameScience	Wird nach ihrem Erfinder Lou Zocchi auch Zocchihedron genannt. Es handelt sich um eine Doppelkugel: die äußere hat 100 Vertiefungen für unterscheidbare Ruhelagen, auf der inneren sind die Werte aufgedruckt und sie enthält Kunststoffschrot für kürzere Rollzeiten. Die Verteilung der Werte ist sehr gleichmäßig, wird aber nicht als wirklich ideal anerkannt.

Sonstige

Neben diesen Familien gibt es einige noch exotischere Modelle, dazu gehören polyederförmige, aber weniger reguläre Körper sowie völlig vereinzelte Konstruktionsprinzipien.

Typ			Form	Ideal	Hersteller	Weitere Informationen
W3			Ellipsoid mit drei eingewölbten Flächen	Ja	GameScience	Neben den Zahlen 1–3 mit RPS für Schere, Stein, Papier beschriftet.
W5			unregelmäßig geformter Körper mit Auflageflächen	nein		Totenkopfform mit 1 - 5 Löchern
W6			Rhomboeder (Parallelepiped)	Ja		Wegen des seltsamen Rollverhaltens als Witz-Würfel verkauft.
W6			In Kubusform eingepasster Mensch	Nein		Beispiel für eine Vielzahl von Varianten, bei der eine Figur näherungsweise in W6-Form eingepasst wurde.
W10			Irreguläres Polyeder	Nein		Körper aus 2 Quadraten und 8 Trapezen, entspricht einem an 2 Ecken abgeschnittenen Oktaeder.
W14			Irreguläres Polyeder	Nein		Körper aus 2 regelmäßigen Sechsecken und 12 unregelmäßigen Fünfecken.
W18			Irreguläres Polyeder	Nein	GameScience	Körper aus 6 Vier- und 12 Sechsecken.
W20			Irreguläres Polyeder	Nein	GameScience	Körper aus 12 Fünfecken, 6 Rhomben und 2 Sechsecken.
W26			Irreguläres Polyeder	Nein	GameScience	Körper aus 2 regelmäßigen Achtecken, 8 Rechtecken und 16 Trapezen.
W?			Schwein	Nein	MB-Spiele	Ein Gummischwein, das im Spiel Schweinerei als Würfel benutzt wird. Durch mehrere mögliche Schräglagen ein hochgradig nichtidealer, aber durchaus den hier verwendeten Definitionen genügender Würfel.

Beschriftung

Zahlen und Augen

Netze der beiden Standard-W6-Beschriftungen. Die Anordnungen der Ziffern im Würfel ist spiegelbildlich zueinander.

Japanischer W6

Üblicherweise werden Spielwürfel mit Zahlen beschriftet, da diese das meistens gewollte Zufallsergebnis sind und bei Verwendung mehrerer Würfel Addition und andere Weiterverarbeitung ermöglichen. Statt arabischer Ziffern werden teils, besonders beim W6, auch runde Markierungen, die Augen, verwendet, die völlig äquivalent zu den Ziffern betrachtet werden können.

Bei den meisten Würfeln, deren Konstruktionsprinzip eindeutige gegenüberliegende Seiten beinhaltet, ist es üblich, die Zahlen so anzuordnen, dass sich je zwei entgegengesetzte Seiten eines n-seitigen Würfels zu n + 1 addieren. Jedoch gibt es Ausnahmen von dieser Regel. Und auch, wenn sie eingehalten wird, ist dadurch die genaue Anordnung der Zahlen noch nicht eindeutig festgelegt, da es meist mehrere Beschriftungen gibt, die diese Regel erfüllen. Für den W6 sind zum Beispiel zwei Orientierungen möglich, die auch beide schon seit der Antike verwendet werden ^[19]. Diese beiden Orientierungen der Ziffern im Würfel sind spiegelbildlich, vgl. Chiralität in der Chemie. Die Ziffern 6 und 9 sind bis auf Drehung identisch. Bei Würfeln, deren Zahlenbereich beide Ziffern verwendet, wird zur einfacheren Unterscheidung meist ein Merkmal hinzugefügt. Üblich sind ein Punkt an der Seite, die als unten zu lesen ist, oder ein Unterstreichen dieser.

In China und teils auch in Japan werden die Standard-Augen-W6 etwas anders bemalt als in Europa. Typisch sind ein besonders großes, rotes Auge für die Eins, eine rote Vier und Anordnung der zwei Augen der Zwei nebeneinander statt diagonal ^[20].

Andere Aufdrucke

Mathematikwürfel

Würfel mit Symbolen

Ein vielfältiges Feld sind auch Würfel mit alternativen Beschriftungen. Halbierte Würfel werden verwendet, um unübliche Seitenzahlen mit verbreiteteren Formen zu simulieren, beispielsweise ein W2, der dadurch erzeugt wird, dass ein W4 mit zwei Einsen und zwei Zweien beschriftet ist. Zehnerstellenwürfel sind Varianten des W10, die statt mit 0–9 mit 00–90, 000–900 oder 0000–9000 oder auch Nachkommastellen (gemäß englischer Notation mit Punkt statt Komma) wie .0–.9, .00–.09 und .000–.009 beschriftet sind. Diese werden in Kombination gewürfelt und die Ergebnisse addiert, sodass man Wurfergebnisse mit mehreren Zehnerstellen erhält. Verbreitet ist vor allem die Verwendung eines W10 mit 00–90 und eines mit 0–9 als simulierter W100 (auch W% genannt) oder eines W10 mit 00-90 und eines mit 1-10, bei dem beide Zahlen addiert werden. Dies kann auch durch zwei verschiedenfarbige W10 mit 0–9, bei denen beispielsweise der rote die Zehnerstelle darstellt, erreicht werden. Zusammengefasste Würfel sind Oktaeder, die die Summe mehrerer Münzwürfe (normalerweise mit 0 und 1) zusammenfassen: Der „W2“ ist je viermal mit der 0 und der 1 beschriftet. Der „2W2“ trägt entsprechend der Wahrscheinlichkeit je zweimal die 0 und 2 und viermal die 1. Der „3W2“ hat je einmal die 0 und 3 und je dreimal die 1 und 2. Theoretisch wären größere Würfel (1x0, 4x1, 6x2, 4x3, 1x4 etc.), doch die Zahl der notwendigen Flächen wäre 2ⁿ und würde schnell sehr groß werden.

Für manche Spiele werden Würfel mit Symbolen, die nicht für Zahlen stehen, verwendet. In der überwiegenden Anzahl der Fälle sind dies W6. Beispiele sind Würfel für Würfel-Poker, Chuck-a-Luck-Varianten oder diverse moderne Brettspiele. Bei Rollenspielen sind Würfel mit Trefferzonen verbreitet. Statt Symbolen werden teils auch einfach Farben verwendet. Auch Kombinationen von Zahlen- und Symbolwürfel existieren, bei denen etwa nur eine Zahl für Werbezwecke durch ein Firmenlogo oder in einem Spiel durch ein Symbol eines besonders wichtigen Ereignisses ersetzt ist.

Da es in der menschlichen Kultur viele genau abgezählte Kategorien gibt, bietet es sich auch an, diese mit passenden Würfeln abzudecken. So existieren W4 mit den vier Grundrechenarten, W8 mit den acht Himmelsrichtungen, W12 mit den Kalendermonaten und ähnliche Produkte.

Wahrscheinlichkeitsrechnung

Wahrscheinlichkeitsverteilung beim Wurf von 1 bis 5 W6

Als Alltagsgegenstände und leicht zu überblickende Systeme sind Würfel beliebte Beispiele in der Wahrscheinlichkeitsrechnung. Umgekehrt liefert die Wahrscheinlichkeitstheorie wichtige Erkenntnisse für den Einsatz von Würfeln in Spielen.

Der Wurf eines einzelnen idealen Würfels, gleich welcher Seitenzahl n, ist das klassische Beispiel für eine Gleichverteilung: jedes der möglichen Ergebnisse hat exakt die gleiche Wahrscheinlichkeit, bei langen Spielen ist also gemäß dem Gesetz der großen Zahlen zu erwarten, dass die Häufigkeiten der Zahlen ähnlich werden. Der Erwartungswert eines solchen Wurfes liegt stets bei $\frac{n+1}{2}$ .

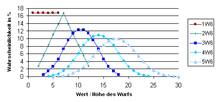
Beim in vielen Spielen verwendeten gleichzeitigen Wurf zweier gleicher Würfel mit Addieren des Ergebnisses nimmt das Wahrscheinlichkeitsdiagramm dagegen die Form eines Dreiecks an, ein Ergebnis ist umso häufiger, je näher es am Mittelwert des Ergebnisbereiches liegt. Nimmt man weitere Würfel hinzu, rundet sich die Kurve ab, die Verteilung nähert sich immer mehr einer Normalverteilung an.

Darüber hinaus verwenden viele Spiele kompliziertere Würfelsysteme, zu denen sich ebenfalls Wahrscheinlichkeitsrechnungen anstellen lassen. Häufige Probleme sind die Wahrscheinlichkeiten für bestimmte Ergebnisklassen (etwa einen Pasch, also zwei gleiche Ergebnisse, beim Monopoly), das Über- oder Unterschreiten einer bestimmten Schranke durch das Gesamtergebnis (in vielen Rollenspielsystemen, genannt „Überwürfeln“ und „Unterwürfeln“) oder die Risikoabwägung zwischen verschiedenen Verteilungen (wenn man etwa in einem Rollenspiel die Wahl zwischen einer Waffe mit Schadenswurf gemäß 2W10 oder einer mit 1W20 hat).

Statistisch interessant sind auch intransitive Würfel. Für jeden dieser unterschiedlich beschrifteten Würfel gibt es einen anderen, der langfristig gegen ihn gewinnt.

Andere Zufallsgeneratoren

Ein sechsseitiger spinner

Ein Dreidel

Würfeln ist nicht das einzige Verfahren, das in Spielen zum Erzeugen von Zufallsergebnissen genutzt wird. Eng mit Würfeln verwandt sind die als spinner oder gambling tops bezeichneten Objekte. Sie bestehen aus einem würfelartigen Körper und einer zentralen Achse, an der sie angedreht werden können und sich dann wie ein Kreisel verhalten, bis sie zur Ruhe kommen und analog wie ein Würfel ein Ergebnis anzeigen; Beispiel hierzu sind der Dreidel und der Nimmgib.

Ein weiterer mechanischer Zufallsgenerator ist das Glücksrad, bei dem sich ein Rad mit Ergebnisbeschriftungen unter einem Zeiger dreht. Auch ist es möglich, die Zufallsentscheidung direkt von Menschen durchführen zu lassen, etwa durch das blinde Ziehen von Losen oder Spielkarten und das Spielen von Schere, Stein, Papier. Heutzutage können auch elektronische Zufallsgeneratoren verwendet werden.

Zitate

• Der Alte würfelt nicht. – Albert Einstein
• Gott würfelt nicht nur mit dem Universum, sondern wirft die Würfel manchmal so, dass wir sie nicht sehen können. – Stephen Hawking
• Alea iacta est. (Der Würfel ist geworfen.) – Julius Caesar

Siehe auch

• Zauberwürfel (Rubik's Cube)

Literatur

• Robert Ineichen: Würfel und Wahrscheinlichkeit – Stochastisches Denken in der Antike. Spektrum Akademischer Verlag, Heidelberg/Berlin/Oxford 1996. ISBN 3-8274-0071-6
• Franz Semrau: Würfel und Würfelspiel im alten Frankreich. Max Niemeyer, Halle a.S. 1910.

Weblinks

 Commons: Spielwürfel – Album mit Bildern und/oder Videos und Audiodateien

• Mathematische Basteleien: Spielwürfel – Deutsche Seite u. a. mit Informationen zu W6-Netzen
• Kevin Cook’s Dice Collection – Weltgrößte private Würfelsammlung, mit Bildern und diversen Informationen (englisch)
• Arjan Verweij Dice – Große Würfelsammlung mit Bildern und einigen historischen Informationen (englisch)

Einzelnachweise

1. ↑ Cultural Heritage News Agency (CHN), 4. Dez. 2004: Iran’s Burnt City Throws up World’s Oldest Backgammon, abrufbar im Persian Journal
2. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 41
3. ↑ British Museum London, Exponate ANE 120839-40, 1935-1-13, 847; ANE 1930-12-13, 534; 1935-1-13, 848; 1929-10-17,438
4. ↑ Peter A. Piccione: In Search of the Meaning of Senet, Archaeology, July/August 1980, Pages 55–58. Wiedergegeben in der Internetpräsenz des Elliot Avedon Museum & Archive of Games.
5. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 43
6. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 66, 53 f., 65
7. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 49
8. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 16 f.
9. ↑ Franz Semrau: Würfel und Würfelspiel im alten Frankreich, S. 25
10. ↑ Franz Semrau: Würfel und Würfelspiel im alten Frankreich, S. 7
11. ↑ Franz Semrau: Würfel und Würfelspiel im alten Frankreich, S. 11
12. ↑ Franz Semrau: Würfel und Würfelspiel im alten Frankreich, S. 30
13. ↑ Franz Semrau: Würfel und Würfelspiel im alten Frankreich, S. 24
14. ↑ AdvancingHordes.com: About GameScience - What does ‘Precision Edged™’ mean? und How fair are Gamescience Dice?
15. ↑ Bob Vollenweider: Casino Dice School – Material, Diceman.ch
16. ↑ dice-play: Casino Dice
17. ↑ Bob Vollenweider: Casino Dice School – Size, Diceman.ch
18. ↑ Bob Vollenweider: Casino Dice School – Security Features, Diceman.ch
19. ↑ Robert Ineichen: Würfel und Wahrscheinlichkeit, S. 42
20. ↑ Arjan Verweij: Dice from China

Dieser Artikel wurde am 20. Januar 2007 in dieser Version in die Liste der exzellenten Artikel aufgenommen.