Iwaniec

Henryk Iwaniec (* 9. Oktober 1947 in Elbląg in Polen) ist ein polnisch-US-amerikanischer Mathematiker, der sich mit analytischer Zahlentheorie beschäftigt.

Leben

Iwaniec studierte an der Universität Warschau, wo er zweimal Ende der 1960er Jahre den Marcinkiewicz-Preis gewann. 1971 schloss er sein Studium ab und wurde im Jahr darauf bei Andrzej Schinzel promoviert. Danach war er am Institut für Mathematik der polnischen Akademie der Wissenschaften. 1976 habilitierte er sich. 1976/77 war er an der Scuola Normale Superiore in Pisa mit einem Stipendium der Accademia dei Lincei und 1979/80 an der Universität Bordeaux. 1983 wurde er Professor und korrespondierendes Mitglied der polnischen Akademie der Wissenschaften. 1983/84 bis 1986 war er am Institute for Advanced Study (IAS) in Princeton und 1984 an der University of Michigan in Ann Arbor sowie Gastprofessor in Boulder. Seit 1987 ist er Professor an der Rutgers University. 1999/2000 war er Gastprofessor am IAS.

Iwaniec sind wesentliche Fortschritte in der analytischen Zahlentheorie zu verdanken. Er bewies 1997 mit John Friedlander durch Anwendung des von ihnen verfeinerten asymptotischen Siebes von Enrico Bombieri^[1], dass es unendlich viele Primzahlen der Form a² + b⁴ gibt (a,b natürliche Zahlen) – der Satz von Bombieri-Friedlander-Iwaniec. Im 19. Jahrhundert hatte einer der Begründer der analytischen Zahlentheorie, Dirichlet, gezeigt, dass es unendlich viele Primzahlen in linearen Folgen der Form 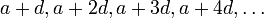$a + d, a + 2 d, a + 3 d, a + 4 d, \ldots$ gibt (a,d teilerfremd zueinander), und auch bei anderen Untermengen der natürlichen Zahlen, die relativ „dicht“ liegen (das heißt neben Primzahlen auch viele zusammengesetzte Zahlen enthalten), wurden ähnliche Sätze bewiesen. Bei dem von Iwaniec und Friedlander untersuchten Problem gelang erstmals ein Durchbruch bei einer relativ „dünnen“ Untermenge der natürlichen Zahlen.

Iwaniec löste auch das Problem von Juri Linnik in der Geometrie der Zahlen, bei dem es sich um die Gleichverteilung der Gitterpunkte auf zweidimensionalen Sphären um den Ursprung handelt, falls der Radius zunimmt. Ein weiteres Arbeitsfeld von Iwaniec ist die analytische Theorie automorpher Formen auf der linearen Gruppe GL(2) und deren L-Funktionen, in der er ebenfalls teilweise mit Friedlander sowie mit W. Duke und Peter Sarnak zusammenarbeitete.

1978 erhielt er den polnischen Staatspreis und 1996 die Sierpinski-Medaille. 2001 erhielt er den Ostrowski-Preis^[2] und 2002 den Colepreis für Zahlentheorie. 1995 wurde er in die American Academy of Arts and Sciences aufgenommen. 1978 und 1986 war er Invited Speaker auf dem ICM.

Er ist Bürger der USA.

Zu seinen Doktoranden zählen Emmanuel Kowalski und Étienne Fouvry.

Schriften

• Topics in Classical Automorphic Forms. Oxford University Press 1997.
• Spectral Methods of Automorphic Forms. Oxford University Press, 2. Auflage, 2003.
• Mit Emmanuel Kowalski: Analytic Number Theory. AMS Colloquium Publications, 2004.

Weblinks

• Iwaniec beim Mathematics Genealogy Project
• Die AMS zum Beweis von Friedlander und Iwaniec

Einzelnachweise

1. ↑ sie überwanden das sogenannte Paritätsproblem dieses Siebes. Friedlander, Iwaniec: Asymptotic Sieve for Primes. Annals of Mathematics, 1998. Using parity sensitive sieve to count prime values of a polynomial. Proceedings National Academy of Sciences, 1997
2. ↑ Iwaniec, Sarnak, and Taylor Receive Ostrowski Prize

Personendaten
NAME	Iwaniec, Henryk
KURZBESCHREIBUNG	polnisch-US-amerikanischer Mathematiker
GEBURTSDATUM	9. Oktober 1947
GEBURTSORT	Elbląg, Polen