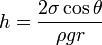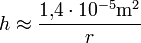Kapillar

Kapillarität oder Kapillareffekt (lat. capillaris, das Haar betreffend) ist das Verhalten von Flüssigkeiten, das sie bei Kontakt mit Kapillaren, z. B. engen Röhren, Spalten oder Hohlräumen, in Feststoffen zeigen.

Beispiel: Taucht man ein Glasröhrchen senkrecht in Wasser, steigt das Wasser in der engen Glasröhre ein Stück gegen die Gravitationskraft nach oben.

Diese Effekte werden durch die Oberflächenspannung von Flüssigkeiten selbst und der Grenzflächenspannung von Flüssigkeiten mit der festen Oberfläche (im Beispiel: des Glases) hervorgerufen.

Effekte

Kapillareffekte in Wasser (links) und Quecksilber.

Die Kapillaraszension tritt bei Flüssigkeiten auf, die das Material des Kapillargefäßes benetzen, wie beispielsweise Wasser auf Glas. Das Wasser steigt in einem Glasröhrchen auf und bildet eine konkave Oberfläche (Meniskus). Dieses Verhalten ist auf die Adhäsionskraft (Kraft, die zwischen zwei Stoffen wirkt) zurückzuführen.

Die Kapillardepression tritt auf, wenn die Flüssigkeit das Material der Gefäßoberfläche nicht benetzt. Beispiele dafür sind Quecksilber auf Glas oder Wasser auf Glas mit eingefetteter Oberfläche. Solche Flüssigkeiten haben in einem Röhrchen einen niedrigeren Pegel als in der Umgebung und eine konvexe Oberfläche.

Je kleiner der Durchmesser, desto größer sind der Kapillardruck und die Steighöhe. Eine Kapillare von 1 µm Durchmesser erzeugt einen Saugdruck von 2,8 bar, entsprechend einer Saughöhe bei benetzendem Wasser von 28 Metern.

Zwei Glasplatten, zwischen denen sich ein Wasserfilm der Dicke 1 µm befindet, werden vom Wasser mit einem Druck von 2,8 bar aneinander gehalten. Deshalb zerbrechen feucht gewordene Objektträger, wenn man versucht, sie auseinander zu ziehen.

Die Flüssigkeit steigt aufgrund von Adhäsionskräften an die Wand des Röhrchens und somit lediglich bis zu dessen Ende, selbst wenn die Kapillarität eine größere Steighöhe erlaubte. Es gibt hier also kein Perpetuum Mobile, bei dem aus einem zu kurzen Glasröhrchen aufgrund des Kapillareffektes laufend Flüssigkeit sprudelte – hierbei würde schließlich potentielle Energie gewonnen.

Formel

Die Steighöhe h (in Metern) einer Flüssigkeitssäule ist gegeben durch:

$h={{2\sigma\cos{\theta}}\over{\rho g r}}$

Dabei ist:

σ = Oberflächenspannung (J/m² oder N/m)

θ = Kontaktwinkel

ρ = Dichte der Flüssigkeit (kg/m³)

g = Beschleunigung durch die Schwerkraft (m/s²)

r = Radius der Röhre (m)

Für eine wassergefüllte Glasröhre, die gegen die Luft auf Meereshöhe offen ist,

σ = 0,0728 J/m² bei 20 °C

θ = 20° = 0,35 rad

ρ = 1000 kg/m³

g = 9,8 m/s²

so ergibt sich für die Steighöhe:

$h\approx \frac{1{,}4 \cdot 10^{-5} \mathrm{m}^{2}}{r}$

Für eine breite Röhre mit r = 1 m folgt daraus eine Steighöhe um nicht merkliche 0,014 mm. Bei 1 cm würde das Wasser um 1,4 mm und bei einer Kapillare mit einem Radius von 0,1 mm um 14 cm steigen.

Molekulare Betrachtung

Grundsätzlich beruht der Effekt der Kapillarität auf den Molekularkräften, die innerhalb eines Stoffes (Kohäsionskräfte) und an der Grenzfläche zwischen einer Flüssigkeit, einem festen Körper (Gefäßwand) und einem Gas (z. B. Luft) auftreten (Adhäsionskräfte). Häufig hat der Kapillareffekt auch die Bedeutung von Oberflächenspannung.

Im Innern eines Körpers heben sich die auf ein bestimmtes Molekül wirkenden Kräfte aus seiner Umgebung gegenseitig auf. An den Rändern jedoch ergibt sich eine resultierende Kraft, die in Abhängigkeit vom jeweiligen Material entweder in die Flüssigkeit hinein oder aus ihr heraus gerichtet ist. Ist die Wirkung der Gefäßwandung gegenüber den Kohäsionskräften in der Flüssigkeit klein, dann zeigt die resultierende Kraft ins Innere der Flüssigkeit. Deren Oberfläche ist an der Kontaktstelle zur Wand nach unten gekrümmt und benetzt die Gefäßwand nicht (z. B. Quecksilber im Glasgefäß). Ist jedoch die Wirkung der Gefäßwandung gegenüber den Kohäsionskräften in der Flüssigkeit groß, dann zeigt die resultierende Kraft in die Gefäßwandung hinein und die Flüssigkeit ist am Rande nach oben gebogen. Die Flüssigkeit benetzt die Wandung (z. B. Wasser oder Petroleum im Glasgefäß).

Praktische Anwendungen

Füller: Ein Beispiel für eine Anwendung ist der Füller oder Füllfederhalter, bzw. seine Feder. Sie besitzt in der Regel auf halber Länge ein kleines, rundes Loch, in dem sich die Tinte sammelt, um von dort durch die Kapillarwirkung durch einen sehr feinen Schlitz an die Spitze transportiert zu werden.

Füllfederhalter

Papier: Es ist nicht möglich, auf einer nichtbenetzenden Oberfläche mit flüssiger Tinte zu schreiben. Daher ist das Schreiben mit einem Füller auf Glas kaum möglich, da die Tinte die Glasoberfläche nicht benetzt und somit nicht an ihr haftet. Auf benetzenden Medien, wie beispielsweise Papier, kann die Tinte haften. Papier saugt mittels Kapillareffekt die Tinte regelrecht auf, es ist sogar möglich über Kopf zu schreiben.

Pflanzen: In Bäumen und anderen Pflanzen wird das Wasser von den Wurzeln aufgenommen und dann bis in die Krone transportiert, wo es aus den Spaltöffnungen der Blätter (oder Nadeln) verdunstet oder für die Photosynthese benötigt wird. Beim Transport gegen die Schwerkraft wirkt die Verdunstung im Oberen Bereich der Pflanze als Sog (Transpirationssog), Kohäsionskräfte des Wassers in der Pflanze verhindern ein Abreißen des Flüssigkeitsstroms, und der Kapillareffekt begünstigt mit dem osmotischen Effekt (Wurzeldruck) den Aufstieg ^[1]. Nach neuen Erkenntnissen können Bäume maximal 130 Meter hoch werden, da dann der osmotische Druck zusammen mit den Kapillarkräften nicht mehr ausreicht, die Schwerkraft zu überwinden ^[2].

Chemie: In der Papierchromatographie nutzt man den Kapillareffekt, indem eine Lösung auf ein Spezialpapier getropft wird und an diesem aufsteigt, wobei Bestandteile der Lösung mitgetragen werden. Aufgrund der unterschiedlichen Laufweite können die Stoffe getrennt werden.

Medizin: Um kleine Mengen Blut abzuzapfen kann man einen kleinen Stich in die Gefäße an den Fingern oder am Ohrläppchen machen und an das austretende Blut ein dünnes Sammelröhrchen halten, in dem das Blut aufgrund des Kapillareffektes aufsteigt und somit gesammelt werden kann.

Textilien: Eine ähnliche Saugwirkung wie beim Papier lässt sich auch bei Putzlappen bzw. Stoffen beobachten. Das gleiche gilt auch für Schwämme. Für Papier, Putzlappen und Schwämme gilt dabei: Je größer die innere Oberfläche (pro Volumen) um so größer auch die Saugwirkung.

Lötkegel

Löten: Auch beim Löten tritt der Effekt auf: Das heiße Lot fließt durch die Kapillarwirkung in den Bereich zwischen Draht und Bohrloch. Auch in ein Drahtgeflecht saugt sich das Lot hinein (Entlötlitze). An der Form des Lötkegels dagegen kann man erkennen, dass es sich um eine benetzende Flüssigkeit handelt. Sollte dieser nicht konkav und auf der Platine flach auslaufend sein, hat man höchstwahrscheinlich eine kalte Lötstelle produziert. Wegen der Kapillarität kann man theoretisch auch „über Kopf“ löten.

Bauwesen: An Häusern und Bauwerken ohne geeignete Schutzmaßnahmen ist im Mauerwerk oft der hier jedoch unerwünschte Kapillar-Effekt zu beobachten, weil die verwendeten Baumaterialien je nach Porengehalt in unterschiedlichem Maße Feuchtigkeit entgegen der Schwerkraft (zumeist aus dem Erdreich bei direktem Bodenkontakt) aufsteigen lassen. Die Wärmeleitfähigkeit des Baumaterials nimmt mit zunehmender Feuchtigkeitsaufnahme zu, so dass der Wärmeverlust des Gebäudes größer wird. Eine große Saugfähigkeit ist beispielsweise in Mauern aus Ziegelsteinen (leichtgebrannt), Porenbeton (sog. „Gasbeton“) und Kalksandsteinen gegeben, eine deutlich geringere Kapillarwirkung ist bei hartgebrannten Ziegelsteinen (Klinker) und Beton zu beobachten. Um den Kapillarstrom in Gebäuden zu unterbrechen, werden im Fundamentbereich wasserdichte Trennschichten, z. B. eine Bitumenbahn, eingebaut.

Quellen

1. ↑ http://www.proholz.at/zuschnitt/22/wassertransport-baum.htm
2. ↑ George W. Koch, Stephen C. Sillett, Gregory M. Jennings, Stephen D. Davis: The limits to tree height. Nature 428, 851–854, 2004, doi:10.1038/nature02417

Literatur und Weblinks

• H. Schubert: Kapillarität in porösen Feststoffsystemen, Springer-Verlag, Berlin, 1982, ISBN 3-540-11835-7
• Vorlesung Medizinische Physik: Oberflächenspannung und Kapillarität, Veterinärmedizinische Universität Wien
• Vorlesung Physik: Fluide Medien – Kapillarität, Universität Ulm
• Popov, Valentin L.: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer-Verlag, 2009, 328 S., ISBN 978-3-540-88836-9.