- Kardinalform
-
Die Begleitmatrix bezeichnet einen Begriff aus der Linearen Algebra.
Definition
Die Begleitmatrix eines normierten Polynoms n-ten Grades
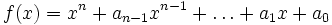 über einem Körper ist die quadratische
über einem Körper ist die quadratische  -Matrix
-MatrixManchmal wird auch die Transponierte von A(f) verwendet, was aber nichts wesentliches ändert. Man nennt diese spezielle Form der Matrix dann auch Kardinalform.
Eigenschaften
Das charakteristische Polynom und das Minimalpolynom von A(f) ist gerade f.
Hat das Polynom f genau n verschiedene Nullstellen
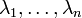 , dann ist A(f) diagonalisierbar:
, dann ist A(f) diagonalisierbar: 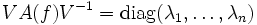 für die Vandermonde-Matrix
für die Vandermonde-Matrix 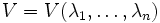 .
.
Wikimedia Foundation.

