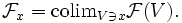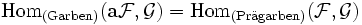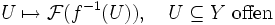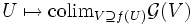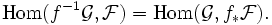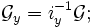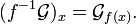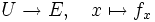- Keim (Mathematik)
-
Eine Garbe ist ein Begriff aus verschiedenen Gebieten der Mathematik wie zum Beispiel der algebraischen Geometrie und Funktionentheorie. Eine Garbe abelscher Gruppen über einem topologischen Raum besteht aus je einer abelschen Gruppe zu jeder offenen Teilmenge des Basisraumes und kompatiblen Einschränkungshomomorphismen zwischen diesen abelschen Gruppen. Entsprechend besteht eine Garbe von Ringen aus einem Ring für jede offene Teilmenge und Ringhomomorphismen. Das einfachste Beispiel einer Garbe ist die Garbe der stetigen reellwertigen Funktionen auf offenen Teilmengen eines topologischen Raumes zusammen mit der Einschränkung der Funktionen auf kleinere offene Teilmengen.
Inhaltsverzeichnis
Definitionen
Um die Definition der "Garbe" zu verstehen, ist es ratsam, sich das Beispiel der Garbe der stetigen Funktionen im Hinterkopf zu halten: F(U) ist die Menge der stetigen Funktionen
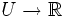 , die Einschränkungsabbildungen (Bilder der Inklusionsabbildungen unter dem Funktor F) sind einfach die Einschränkungen der Funktionen auf kleinere Bereiche.
, die Einschränkungsabbildungen (Bilder der Inklusionsabbildungen unter dem Funktor F) sind einfach die Einschränkungen der Funktionen auf kleinere Bereiche.Prägarbe
Eine Prägarbe besteht aus einer Menge (bzw. abelschen Gruppe, Modul, Ring)
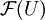 für jede offene Teilmenge
für jede offene Teilmenge 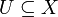 zusammen mit Einschränkungsabbildungen
zusammen mit Einschränkungsabbildungen 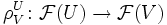 für zwei offene Teilmengen
für zwei offene Teilmengen 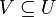 ; dabei müssen die Einschränkungsabbildungen in der "offensichtlichen" Weise zusammenpassen:
; dabei müssen die Einschränkungsabbildungen in der "offensichtlichen" Weise zusammenpassen: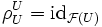
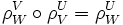 für offene Teilmengen
für offene Teilmengen 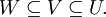
Für die Einschränkung
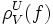 eines Schnittes
eines Schnittes 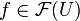 auf eine offene Teilmenge
auf eine offene Teilmenge 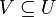 schreibt man auch
schreibt man auch 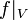 .
.Garbe
Eine Garbe ist eine Prägarbe, bei der die Daten "lokal" sind, d.h. die folgenden beiden Bedingungen erfüllt sind:
- Lokale Übereinstimmung impliziert globale Übereinstimmung: Sind f und g Schnitte von
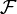 über U und {Vi} eine Überdeckung von U, und gilt
über U und {Vi} eine Überdeckung von U, und gilt
-
- für alle i, so gilt f = g.
- Zusammenpassende lokale Daten lassen sich "verkleben": Sind Schnitte
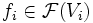 gegeben, so dass die Einschränkungen von fi und fj auf
gegeben, so dass die Einschränkungen von fi und fj auf 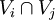 übereinstimmen, so gibt es einen Schnitt
übereinstimmen, so gibt es einen Schnitt 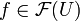 , so dass
, so dass
-
- für alle i gilt.
Aus der ersten Bedingung folgt, dass f in der zweiten Bedingung durch die fi eindeutig bestimmt ist.
Kategorientheoretisch
Es sei X ein topologischer Raum. Die Kategorie
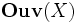 habe als Objekte die offenen Teilmengen von X. Die Morphismen seien gegeben durch die mengentheoretische Inklusion zwischen zwei offenen Mengen U und V aus
habe als Objekte die offenen Teilmengen von X. Die Morphismen seien gegeben durch die mengentheoretische Inklusion zwischen zwei offenen Mengen U und V aus 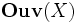 Falls U nicht in V enthalten ist, sei der Morphismus die leere Menge. Eine Prägarbe
Falls U nicht in V enthalten ist, sei der Morphismus die leere Menge. Eine Prägarbe 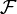 auf X mit Werten in einer Kategorie C ist ein kontravarianter Funktor
auf X mit Werten in einer Kategorie C ist ein kontravarianter Funktor 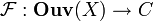 . Eine Prägarbe
. Eine Prägarbe 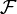 heißt Garbe, falls das folgende Diagramm für jede offene Teilmenge
heißt Garbe, falls das folgende Diagramm für jede offene Teilmenge 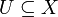 und jede Überdeckung {Vi} von U exakt ist:
und jede Überdeckung {Vi} von U exakt ist:d.h. dass
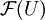 der Differenzkern der beiden rechten Pfeile ist.
der Differenzkern der beiden rechten Pfeile ist.Die Elemente von
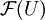 heißen (lokale) Schnitte von
heißen (lokale) Schnitte von 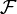 über U, die Elemente von
über U, die Elemente von 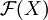 globale Schnitte. Statt
globale Schnitte. Statt 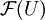 schreibt man auch
schreibt man auch 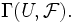
(Der Begriff "Garbe" ist nur definiert, wenn C Produkte besitzt.)
Halme und Keime
Es sei C eine Kategorie algebraischer Strukturen, die durch endliche projektive Limites definiert sind, also z.B. (abelsche) Gruppen, Ringe, Moduln. Insbesondere existieren pseudofiltrierende Kolimites in C, und ihre zugrundeliegenden Mengen stimmen mit den Kolimites der zugrundeliegenden Mengen der Einzelobjekte überein.
Für jeden Punkt
 ist der Halm
ist der Halm 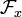 einer Prägarbe
einer Prägarbe 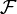 im Punkt x definiert als
im Punkt x definiert alsElemente des Halms heißen Keime.
Keime sind also Äquivalenzklassen von lokalen Schnitten über offenen Umgebungen von x, wobei Schnitte äquivalent sind, wenn sie bei Einschränkung auf eine kleinere Umgebung gleich werden.
Vergarbung
Ist
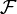 eine Prägarbe auf einem topologischen Raum X, so gibt es eine Garbe
eine Prägarbe auf einem topologischen Raum X, so gibt es eine Garbe 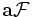 , die Vergarbung von oder assoziierte Garbe zu
, die Vergarbung von oder assoziierte Garbe zu 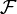 , so dass für jede Garbe
, so dass für jede Garbe 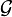
gilt.
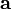 ist also linksadjungiert zum Vergissfunktor
ist also linksadjungiert zum Vergissfunktor 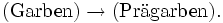
Es gibt keine einheitliche Notation für den Vergarbungsfunktor.
Direkte Bilder und Urbildgarben
Ist
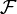 eine Garbe auf einem topologischen Raum X und
eine Garbe auf einem topologischen Raum X und 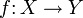 eine stetige Abbildung, so ist
eine stetige Abbildung, so isteine Garbe auf Y, die mit
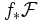 bezeichnet wird und direktes Bild oder auch Bildgarbe von
bezeichnet wird und direktes Bild oder auch Bildgarbe von 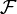 unter f heißt.
unter f heißt.Ist
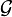 eine Garbe auf Y, so ist die assoziierte Garbe zu
eine Garbe auf Y, so ist die assoziierte Garbe zueine Garbe auf X, die Urbildgarbe, die mit
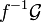 bezeichnet wird.
bezeichnet wird.Ist
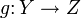 eine weitere stetige Abbildung, so sind die Funktoren
eine weitere stetige Abbildung, so sind die Funktoren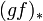 und
und 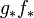
sowie die Funktoren
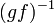 und
und 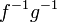
natürlich äquivalent.
Die Funktoren
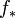 und
und 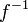 sind adjungiert: Ist
sind adjungiert: Ist 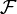 eine Garbe auf X und
eine Garbe auf X und 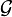 eine Garbe auf
eine Garbe auf 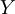 , so ist
, so istHalme sind spezielle Garbenurbilder: Bezeichnet iy die Inklusion
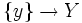 eines Punktes, so ist
eines Punktes, so istdabei wurde die Garbe
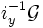 auf dem einpunktigen Raum
auf dem einpunktigen Raum 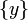 mit ihren globalen Schnitten identifiziert. Infolgedessen ist das Garbenurbild kompatibel mit Halmen:
mit ihren globalen Schnitten identifiziert. Infolgedessen ist das Garbenurbild kompatibel mit Halmen:Diese Beziehung ist auch der Grund dafür, dass
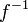 trotz der komplizierteren Definition der einfacher zu verstehende Funktor ist: in einem gewissen Sinn ist Kohomologie das Studium des Funktors
trotz der komplizierteren Definition der einfacher zu verstehende Funktor ist: in einem gewissen Sinn ist Kohomologie das Studium des Funktors 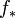 .
.Der étale Raum einer Garbe
Zu einer Garbe
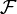 von Mengen sei ein topologischer Raum E über X wie folgt definiert:
von Mengen sei ein topologischer Raum E über X wie folgt definiert:- Die zugrundeliegende Menge ist die disjunkte Vereinigung aller Halme von
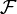 ; die Abbildung
; die Abbildung 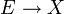 bilde
bilde 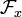 auf
auf  ab.
ab. - Die Topologie auf E ist die stärkste Topologie, für die die Abbildungen
-
- für jeden Schnitt
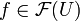 über einer offenen Menge
über einer offenen Menge 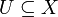 stetig sind.
stetig sind.
Dann gibt es eine Bijektion zwischen den Schnitten von
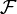 über einer offenen Menge
über einer offenen Menge 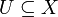 und den Schnitten von
und den Schnitten von 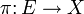 über U, d.h. den stetigen Abbildungen
über U, d.h. den stetigen Abbildungen 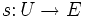 , für die
, für die 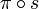 gleich der Inklusion
gleich der Inklusion 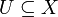 ist.
ist.Beispiele
- Die stetigen Funktionen mit kompaktem Träger bilden keine Prägarbe, weil die Einschränkung einer Funktion mit kompaktem Träger auf eine offene Teilmenge im Allgemeinen nicht wieder kompakten Träger hat.
- Die Prägarbe, die jeder offenen Teilmenge von
 die abelsche Gruppe
die abelsche Gruppe 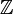 zuordnet, ist keine Garbe: Ist
zuordnet, ist keine Garbe: Ist 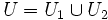 mit U1 = (1,2) und U2 = (3,4), so lassen sich der Schnitt 5 über U1 und der Schnitt 7 über U2 nicht zu einem Schnitt über U "verkleben".
mit U1 = (1,2) und U2 = (3,4), so lassen sich der Schnitt 5 über U1 und der Schnitt 7 über U2 nicht zu einem Schnitt über U "verkleben".
- Die Garbe
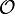 der holomorphen Funktionen auf
der holomorphen Funktionen auf  ist eine Garbe von Ringen (eine "Ringgarbe"): der Halm im Nullpunkt kann mit dem Ring der konvergenten Potenzreihen
ist eine Garbe von Ringen (eine "Ringgarbe"): der Halm im Nullpunkt kann mit dem Ring der konvergenten Potenzreihen 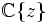 identifiziert werden, d.h. der Potenzreihen, deren Konvergenzradius nicht Null ist. Die anderen Halme entstehen durch Koordinatenwechsel (d.h. ersetze z durch z − a).
identifiziert werden, d.h. der Potenzreihen, deren Konvergenzradius nicht Null ist. Die anderen Halme entstehen durch Koordinatenwechsel (d.h. ersetze z durch z − a).
- Es sei X = {η,s} der topologische Raum mit zwei Punkten, von denen s abgeschlossen ist und η nicht. Dann ist eine Garbe durch die zwei Mengen
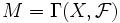 und
und 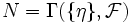 zusammen mit einer Abbildung
zusammen mit einer Abbildung 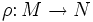 bestimmt, und umgekehrt kann man diese Daten beliebig vorgeben und erhält eine Garbe. Die Halme von
bestimmt, und umgekehrt kann man diese Daten beliebig vorgeben und erhält eine Garbe. Die Halme von 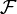 sind
sind
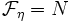 und
und 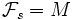 .
.
- Es sei
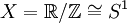 und zu offenem
und zu offenem 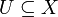 sei
sei 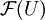 die Menge aller Funktionen, die lokal Steigung 1 haben, das sind alle
die Menge aller Funktionen, die lokal Steigung 1 haben, das sind alle 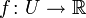 mit
mit 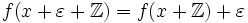 , sofern beide Seiten definiert sind und
, sofern beide Seiten definiert sind und 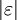 hinreichend klein ist. Dies ist eine Garbe, bei der jeder Halm
hinreichend klein ist. Dies ist eine Garbe, bei der jeder Halm 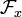 isomorph zu
isomorph zu  und auch
und auch 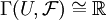 für jede zusammenhängende offene echte Teilmenge
für jede zusammenhängende offene echte Teilmenge 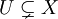 . Es gibt jedoch keine globalen Schnitte,
. Es gibt jedoch keine globalen Schnitte, 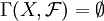 . Dadurch ist dies „nur“ eine mengenwertige und keine abelsche-Gruppen-wertige Garbe.
. Dadurch ist dies „nur“ eine mengenwertige und keine abelsche-Gruppen-wertige Garbe.
Verallgemeinerung
Der Begriff der Garbe lässt sich allgemeiner im Kontext von Grothendieck-Topologien fassen.
Literatur
Francisco Miraglia: An Introduction to Partially Ordered Structures and Sheaves, Polimetrica 2006, ISBN 8876990356.
Wikimedia Foundation.

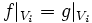
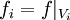
![\mathcal F(U)\rightarrow \prod\mathcal F(V_i)\,\begin{matrix}\rightarrow\\[-,7em]\rightarrow\end{matrix}\,\prod\mathcal F(V_i\cap V_j),](/pictures/dewiki/57/96b4f882df7a4c4d1926f786fd56182a.png)