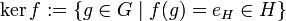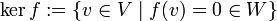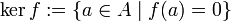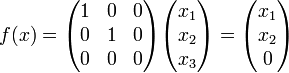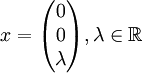Kokern

Im mathematischen Teilgebiet der Algebra ist der Kern einer Abbildung die Menge der Elemente, die auf die 0 oder allgemeiner das neutrale Element abgebildet werden. Der Kern wird häufig auch als Nullraum bezeichnet.

• Ist 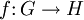$f\colon G \rightarrow H$ ein Gruppenhomomorphismus, so wird die Menge

$\ker f := \{ g\in G \mid f(g) = e_H\in H \}$

aller Elemente von G, die auf das neutrale Element e_H von H abgebildet werden, Kern von f genannt. Er ist ein Normalteiler in G.

• Ist 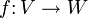$f\colon V\to W$ eine lineare Abbildung von Vektorräumen (oder ein Homomorphismus abelscher Gruppen oder allgemeiner Moduln), dann heißt die Menge

$\ker f := \{ v \in V \mid f(v) = 0 \in W\}$

der Kern von f. Er ist ein f-invarianter Untervektorraum von V.

• Ist 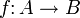$f\colon A\to B$ ein Ringhomomorphismus, so ist die Menge

$\ker f :=\{ a\in A\mid f(a) = 0\}$

der Kern von f. Er ist ein zweiseitiges Ideal in A.

Der Kern ist von zentraler Bedeutung im Homomorphiesatz.

Bedeutung

Eine lineare Abbildung bzw. ein Homomorphismus ist genau dann injektiv, wenn der Kern nur aus dem Nullvektor bzw. dem neutralen Element besteht.

Beispiel (lineare Abbildung von Vektorräumen)

Wir betrachten die lineare Abbildung 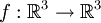$f: \mathbb R^3 \to \mathbb R^3$, die durch

$f(x)= \begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}\begin{pmatrix} x_1\\x_2\\ x_3\end{pmatrix} = \begin{pmatrix} x_1\\x_2\\ 0\end{pmatrix}$

definiert ist. Die Abbildung f bildet genau die Vektoren der Form

$x=\begin{pmatrix}0\\0\\\lambda \end{pmatrix}, \lambda \in \mathbb R$

auf den Nullvektor ab und andere nicht. Der Kern von f ist also die Menge

$\operatorname{ker}\, (f) = \left\{ \begin{pmatrix}0\\0\\\lambda \end{pmatrix}, \lambda \in \mathbb R\right\}$.

Geometrisch ist der Kern in diesem Fall eine Gerade (die z-Achse) und hat demnach die Dimension 1. Die Dimension des Kerns wird auch als Defekt bezeichnet und kann mit Hilfe des Rangsatzes explizit berechnet werden.

Verallgemeinerungen

In einer Kategorie mit Nullobjekten ist ein Kern eines Morphismus f: X → Y der Differenzkern des Paares (f, 0), d.h. charakterisiert durch die folgende universelle Eigenschaft:

• Ist t: T → X ein Morphismus, so dass ft = 0 ist, so faktorisiert t über ker f.

In der universellen Algebra ist der Kern einer Abbildung f: A → B die durch f induzierte Äquivalenzrelation auf A, also die Menge ker(f):={(x,y): f(x)=f(y)}. Wenn A und B algebraische Strukturen gleichen Typs sind (z.B.: A und B sind Verbände) und f ein Homomorphismus von A nach B ist, dann ist die Äquivalenzrelation ker(f) auch eine Kongruenzrelation. Umgekehrt zeigt man auch leicht, dass jede Kongruenzrelation Kern eines Homomorphismus ist.

Kokern

Der Kokern ist der duale Begriff zum Kern.

Ist f: V → W eine lineare Abbildung von Vektorräumen über einem Körper, so ist der Kokern von f der Quotient von W nach dem Bild von f.

Entsprechend ist der Kokern für Homomorphismen abelscher Gruppen oder Moduln über einem Ring definiert.

Der Kokern erfüllt die folgende universelle Eigenschaft: Jeder Homomorphismus t: W → T, für den tf = 0 gilt, faktorisiert über den Kokern von f.

Diese Eigenschaft ist auch die Definition für den Kokern in beliebigen Kategorien mit Nullobjekten. In abelschen Kategorien stimmt der Kokern mit dem Quotienten nach dem Bild überein.