Lineare Gleichung

Eine lineare Gleichung ist eine mathematische Bestimmungsgleichung, in der ausschließlich Linearkombinationen der Unbekannten vorkommen. Typischerweise sind die Unbekannten einer linearen Gleichung Skalare, meist reelle Zahlen. Im einfachsten Fall einer skalaren Unbekannten x besitzt eine lineare Gleichung die Form

$a \cdot x = b$

wobei a und b Konstanten sind. Es gibt aber auch lineare Gleichungen mit mehreren Unbekannten und mit anderen mathematischen Objekten als Unbekannten, beispielsweise Folgen (lineare Differenzengleichungen), Vektoren (lineare Gleichungssysteme) oder Funktionen (lineare Differentialgleichungen). Im allgemeinen Fall besitzt eine lineare Gleichung die Form

T(x) = b

wobei T ein linearer Operator ist.

Homogene lineare Gleichungen sind spezielle lineare Gleichungen, bei denen der konstante Term b der Gleichung gleich Null ist. Die Lösungen einer homogenen linearen Gleichung bilden einen Untervektorraum des Vektorraums der Unbekannten und besitzen damit besondere Eigenschaften, wie die Gültigkeit des Superpositionspinzips. Die Lösungen einer inhomogenen linearen Gleichung bilden hingegen einen affinen Unterraum, so lässt sich jede Lösung einer inhomogenen linearen Gleichung als Summe der Lösung der zugehörigen homogenen Gleichung und einer Partikulärlösung darstellen. Der Lösungsraum einer linearen Gleichung kann über den Kern und den Kokern der linearen Abbildung charakterisiert werden.

Lineare Gleichungen und deren Lösungen werden insbesondere in der Linearen Algebra und der Linearen Funktionalanalysis studiert, sie spielen aber auch in der Zahlentheorie eine Rolle.

Skalare lineare Gleichungen

Häufig sind die Unbekannten bei linearen Gleichungen Skalare (meist reelle oder komplexe Zahlen). Solche lineare Gleichungen sind dann spezielle algebraische Gleichungen vom Grad 1.

Lineare Gleichungen mit einer Unbekannten

Eine skalare Gleichung mit einer Unbekannten x heißt linear, wenn sie durch Äquivalenzumformungen in die Form

$a \cdot x \; = \; b$

gebracht werden kann. Hierbei sind a und b Konstanten, die nicht von x abhängen.

Ist $a\neq 0$, kann der Wert der Unbekannten x, mit dem die Gleichung erfüllt ist, bestimmt werden, indem auf beiden Seiten durch a geteilt wird:

$x \; = \; \frac{b}{a}$

Falls a = 0 und $b\neq 0$ sind, besitzt die Gleichung keine Lösung. Falls a = 0 und b = 0 sind, gibt es unendlich viele Lösungen, also jedes x erfüllt die Gleichung.

Beispiele

Um die lineare Gleichung

$7 \cdot x - 9 \; = \; 4 \cdot x + 15.$

zu lösen bringt man sie zunächst durch Äquivalenzumformungen in obige Normalform. Hierzu sammelt man alle Terme mit der Unbekannten x auf der linken Seite und alle anderen Terme auf der rechten Seite. Dazu addiert man auf beiden Seiten die Zahl 9, was

$7 \cdot x \; = \; 4 \cdot x + 24\,$

ergibt, und subtrahiert von beiden Seiten den Term $4 \cdot x$, wodurch man die Normalform

$3 \cdot x \; = \; 24$

erhält. Nun dividiert man beide Seiten durch 3, sodass auf der linken Seite nur noch die Unbekannte x übrig bleibt, und es ergibt sich als Lösung

$x \; = \; \frac{24}{3} \; = \; 8.$

Die lineare Gleichung

$0 \cdot x \; = \; 7$

besitzt keine Lösung, während die lineare Gleichung

$0 \cdot x \; = \; 0$

für jedes x erfüllt wird.

Lineare Gleichungen mit zwei Unbekannten

Die Lösungsmenge der linearen Gleichung $\scriptstyle 3x+4y=12$

Eine skalare Gleichung mit zwei Unbekannten x und y heißt linear, wenn sie durch Äquivalenzumformungen in die Form

$a \cdot x + b \cdot y \; = \; c$

gebracht werden kann, wobei a, b und c Konstanten sind. Die Lösungen bilden Geraden im zweidimensionalen Raum, sofern nicht sowohl a = 0, als auch b = 0 sind. Andernfalls ist die Lösungsmenge entweder der ganze zweidimensionale Raum (c = 0) oder leer $(c \neq 0)$.

Die Lösung einer solchen Gleichung wird oft in Parameterdarstellung angegeben. Hierzu löst man die Gleichung nach einer der Unbekannten auf, beispielsweise y, was sofern $b \neq 0$

$y \; = \; (c - a \cdot x) / b$

ergibt, und fasst die andere Unbekannte x als freien Parameter t auf. Damit kann man die Lösung als

$x \; = \; t$    und    $y \; = \; (c - a \cdot t) / b$    mit    $t \in \mathbb{R}$

schreiben. Auf diese Weise wird sichtbar, dass, obwohl die Gleichung zwei Unbekannte enthält, der Lösungsraum nur eindimensional ist, also lediglich von einem Parameter t abhängt. Die Parameterdarstellung selbst ist nicht eindeutig. Ist $a \neq 0$ kann man die Gleichung auch nach x auflösen und y als freien Parameter wählen. Auch andere Parametrisierungen sind möglich, dennoch wird durch sie die gleiche Lösungsmenge beschrieben.

Beispiel

Die Lösungsmenge für die lineare Gleichung

$3 \cdot x + 4 \cdot y \; = \; 12$

ist durch Auflösen nach y als

$x \; = \; t$    und    $y \; = \; (12 - 3 \cdot t)/4$    mit    $t \in \mathbb{R}.$

gegeben. Den Funktionsgraph der beschriebenen Gerade erhält man dann über die Geradengleichung

$f(x) \; = \; (12 - 3 \cdot x)/4 \; = \; -(3/4) \cdot x + 3.$

Lineare Gleichungen mit mehreren Unbekannten

Die Lösung einer reellen linearen Gleichung mit drei Unbekannten ist im allgemeinen eine Ebene

Allgemein heißt eine skalare Gleichung mit n Unbekannten $x_1, x_2, \ldots , x_n$ linear, wenn sie durch Äquivalenzumformungen in die Form

$a_1 x_1 + a_2 x_2 +\;\cdots \; + a_n x_n \; = \; b$

gebracht werden kann, wobei $a_1, a_2, \ldots , a_n$ und b Konstanten sind. Es dürfen also ausschließlich Linearkombinationen der Unbekannten auftreten. Die Lösungen solcher Gleichungen sind im allgemeinen (n − 1)-dimensionale Teilmengen (Hyperebenen) des zugehörigen n-dimensionalen Raums. Falls $a_1 = a_2 = \cdots = a_n = 0$ ist die Lösungsmenge entweder der ganze n-dimensionale Raum (b = 0) oder leer $(b \neq 0)$.

Die Parameterdarstellung der Lösungsmenge erhält man im allgemeinen Fall wiederum dadurch, dass man die Gleichung nach einer der Unbekannten, beispielsweise x_n wenn $a_n \neq 0$, auflöst,

$x_n\; = \; (b - a_1 x_1 -\;\cdots \; - a_{n-1} x_{n-1})/a_n,$

und die anderen Unbekannten als freie Parameter t₁ bis t_{n − 1} auffasst. Damit ist die Lösungsmenge gegeben als

$x_1 \; = \; t_1, \; \ldots , \; x_{n-1} \; = \; t_{n-1}, \; x_n\; = \; (b - a_1 t_1 -\;\cdots \; - a_{n-1} t_{n-1})/a_n$    mit    $t_1, \ldots , t_{n-1} \in \mathbb{R}.$

Dadurch, dass n − 1 Parameter frei wählbar sind, ist der Lösungsraum (n − 1)-dimensional. Auch hier ist die Parameterdarstellung nicht eindeutig, man kann die Gleichung auch nach einer der anderen Unbekannten, sofern der zugehörige Koeffizient ungleich Null ist, auflösen oder eine andere Parametrisierung wählen.

Beispiel

Die Lösungsmenge der linearen Gleichung mit drei Unbekannten

$3 \cdot x_1 + 2 \cdot x_2 + x_3 \; = \; 7$

ist eine Ebene im dreidimensionalen Raum mit Darstellung

$x_1 \; = \; t_1, \; x_2 \; = \; t_2, \; x_3\; = \; 7 - 3 \cdot t_1 - 2 \cdot t_2$    mit    $t_1, t_2 \in \mathbb{R}.$

Allgemeine lineare Gleichungen

Lineare Operatoren

Allgemein werden lineare Gleichungen über lineare Operatoren definiert. Eine Gleichung der Form

$T(x) \; = \; b$

heißt dabei linear, wenn T ein linearer Operator ist und wenn b unabhängig von x ist. Der Operator $T: V \rightarrow W$ bildet dabei von einem Vektorraum V in einen Vektorraum W ab, wobei $x\in V$ und $b\in W$ sind. Beide Vektorräume sind dabei über einem gemeinsamen Körper K definiert. Ein Operator ist linear, wenn für Konstanten $\lambda, \mu \in K$

$T\left(\lambda x + \mu y\right) \; = \; \lambda T\left( x \right) + \mu T\left( y\right)$

gilt.

Beispiel

Ist $V = \mathbb{R}^n$ und $W = \mathbb{R}$, dann ist $x = (x_1, \ldots , x_n) \in \mathbb{R}^n$ ein reeller Vektor und $b \in \mathbb{R}$ eine reelle Zahl. Wählt man nun für T das lineare Funktional

$T(x) \; = \; a \cdot x$

mit konstantem Vektor $a = (a_1, \ldots, a_n) \in \mathbb{R}^n$, wobei $( \cdot )$ das Skalarprodukt der beiden Vektoren ist, dann erhält man die lineare Vektorgleichung

$a \cdot x \; = \; b$

welche äquivalent zur obigen skalaren linearen Gleichung mit n Unbekannten ist. Die Linearität von T folgt dabei direkt aus der Linearität der Skalarmultiplikation

$T(\lambda x+\mu y) \; = \; a \cdot (\lambda x+\mu y) \; = \; \lambda(a \cdot x)+\mu(a \cdot y) \; = \; \lambda T(x)+\mu T(y)$

Homogenität

Eine homogene und eine inhomogene skalare lineare Gleichung mit zwei Unbekannten $\scriptstyle x_1$ und $\scriptstyle x_2$

Eine lineare Gleichung heißt homogen, falls b = 0 ist, also wenn sie die Form

$T(x) \; =\; 0$

besitzt, ansonsten heißt eine lineare Gleichung inhomogen. Homogene lineare Gleichungen besitzen mindestens die triviale Lösung

$x \; = \; 0,$

da

$T(0) \; = \; T(0 \cdot 0) \; = \; 0 \cdot T(0) \; = \; 0$

gilt. Umgekehrt werden inhomogene lineare Gleichungen nie durch die triviale Lösung erfüllt.

Beispiel

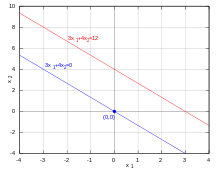
Die Lösung der homogenen linearen Gleichung mit zwei Unbekannten x₁ und x₂

$3 x_1 + 4 x_2 \; = \; 0$

ist eine Gerade im zweidimensionalen Raum, die durch den Nullpunkt geht. Die Lösung der inhomogenen Gleichung

$3 x_1 + 4 x_2 \; = \; 12$

ist eine dazu parallele Gerade, die aber nicht den Nullpunkt enthält.

Superposition

Superpositionsprinzip bei der linearen Gleichung $\scriptstyle x_1 - 2 x_2 = 10$: Lösung der homogenen Gleichung (blau), Partikulärlösung (grün) und Lösung der inhomogenen Gleichung (rot)

→ Hauptartikel: Superposition (Mathematik)

Homogene lineare Gleichungen besitzen die Superpositionseigenschaft: seien $\hat{x}$ und $\bar{x}$ zwei Lösungen einer homogenen linearen Gleichung, dann ist auch $\hat{x}+\bar{x}$ eine Lösung dieser Gleichung. Allgemein gilt sogar, dass alle Linearkombinationen $c\hat{x}+d\bar{x}$ von Lösungen einer homogenen linearen Gleichung mit Konstanten c und d diese Gleichung lösen, da

$T(c\hat{x}+d\bar{x}) \; = \; T(c\hat{x})+T(d\bar{x}) \; = \; cT(\hat{x}) + dT(\bar{x}) \; = \; 0 + 0 \; = \; 0$

gilt. Durch die Einbeziehung von x = 0 und die Superpositionseigenschaft bilden die Lösungen einer homogenen linearen Gleichung einen Untervektorraum von V.

Weiterhin lässt sich die Lösung einer inhomogenen Gleichung als Summe der Lösung der zugehörigen homogenen Gleichung und einer Partikulärlösung darstellen: sei $\bar{x}$ eine konkrete Lösung einer inhomogenen linearen Gleichung und sei y die allgemeine Lösung des zugehörigen homogenen Problems, dann ist $y+\bar{x}$ die allgemeine Lösung der inhomogenen Gleichung, da

$T(y+\bar{x}) \; = \; T(y) + T(\bar{x}) \; = \; 0 + b \; = \; b$

gilt. Die Lösungen einer inhomogenen linearen Gleichung bilden damit einen affinen Unterraum über dem Vektorraum der zugehörigen homogenen Gleichung.

Umgekehrt gilt entsprechend: sind $\hat{x}$ und $\bar{x}$ zwei Lösungen einer inhomogenen linearen Gleichung, dann löst $\hat{x} - \bar{x}$ die zugehörige homogene Gleichung, da

$T(\hat{x}-\bar{x}) \; = \; T(\hat{x}) - T(\bar{x}) \; = \; b - b \; = \; 0$

gilt.

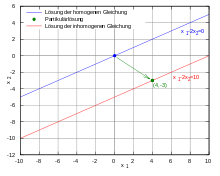
Beispiel

Eine konkrete Lösung der inhomogenen Gleichung

$x_1 - 2 x_2 \; = \; 10$

ist

$\bar{x}_1 = 4, \bar{x}_2 \; = \; -3$

Sind nun y = (y₁,y₂) die Lösungen der zugehörigen homogenen Gleichung

$y_1 - 2 y_2 \; = \; 0$,

also alle y mit y₁ = 2y₂, dann wird die inhomogene Gleichung allgemein gelöst durch

$x \; = \; y + \bar{x} \; = \; (y_1 + \bar{x}_1, y_2 + \bar{x}_2) \; = \; (2 y_2 + 4, y_2 - 3) \; = \; (2t + 4, t - 3)$    mit    $t \in \mathbb{R}.$

Dimension des Lösungsraums

Der Lösungsraum einer homogenen linearen Gleichung wird als Kern ker(T) des linearen Operators bezeichnet, seine Dimension nennt man auch Defekt. Aufgrund des Rangsatzes gilt für die Dimension des Lösungsraums einer endlich-dimensionalen homogenen linearen Gleichung

dim(ker(T)) = dim(V) − rang(T).

Dabei ist rang(T) der Rang des Operators, also die Dimension seines Bildes. Das Bild eines Operators ist die Menge der Werte, die T(x) für $x \in V$ annehmen kann.

Aufgrund der Superpositionseigenschaft ist die Dimension des Lösungsraums einer inhomogenen linearen Gleichung gleich der der zugehörigen homogenen Gleichung, sofern eine Partikulärlösung existiert. Dies ist genau dann der Fall, wenn die rechte Seite b im Bild des Operators liegt, also $b \in T(V)$ gilt. Der Kokern des linearen Operators coker(T) = W / T(V) beschreibt gerade den Raum der Bedingungen, die die rechte Seite einer linearen Gleichung erfüllen muss, damit die Gleichung lösbar ist. Seine Dimension ist

dim(coker(T)) = dim(W) − rang(T).

Beispiele

Wählt man als Vektorräume $V = \mathbb{R}^3$ und $W = \mathbb{R}$, sowie als linearen Operator

T(x) = a₁x₁ + a₂x₂ + a₃x₃,

wobei zumindest einer der Koeffizienten a₁,a₂,a₃ ungleich Null sei, dann ist das Bild von T der ganze Raum W und somit

$\mathrm{dim}(\mathrm{ker}(T)) = \dim(\mathbb{R}^3) - \dim(\mathbb{R}) = 3 - 1 = 2.$

Der Lösungsraum der homogenen linearen Gleichung T(x) = 0 hat also Dimension 2 und ist eine Ebene im dreidimensionalen Raum. Auch der Lösungsraum der inhomogenen Gleichung T(x) = b ist hier eine Ebene, da die Gleichung, wenn beispielsweise $a_1 \neq 0$ ist, die Partikulärlösung (b / a₁,0,0) besitzt. Der Kokern hat hier Dimension 0, die Gleichung ist also für beliebiges b lösbar.

Wählt man stattdessen

T(x) = 0x₁ + 0x₂ + 0x₃,

dann werden alle Vektoren aus V auf die Null abgebildet und es gilt

$\mathrm{dim}(\mathrm{ker}(T)) = \dim(\mathbb{R}^3) - \dim(\{ 0 \}) = 3 - 0 = 3.$

Der Lösungsraum der zugehörigen homogenen linearen Gleichung ist also der gesamte dreidimensionale Raum. Der Lösungsraum der inhomogenen Gleichung ist in diesem Fall leer, da die Gleichung nur für b = 0 eine Lösung besitzt. Der Kokern hat Dimension 1.

Wichtige Typen linearer Gleichungen

Lineare Diophantische Gleichungen

Lösungen der linearen Diophantischen Gleichung $\scriptstyle 2x_1+3x_2=26$

→ Hauptartikel: Lineare Diophantische Gleichung

Wählt man Vektorräume $V = \mathbb{Z}^n$ und $W = \mathbb{Z}$ über den ganzen Zahlen und

$T(x) \; = \; a \cdot x$

mit konstantem Koeffizientenvektor $a \in \mathbb{Z}^n$, erhält man die linearen Diophantischen Gleichungen

$a_1 x_1 + a_2 x_2 +\;\cdots \; + a_n x_n \; = \; b,$

von denen ganzzahlige Lösungen $x = (x_1, \ldots , x_n) \in \mathbb{Z}^n$ gesucht werden. Lineare Diophantische Gleichungen besitzen Lösungen, wenn der größte gemeinsame Teiler der Koeffizienten a₁ bis a_n ein Teiler der rechten Seite b ist, also wenn

$ggT(a_1, \ldots , a_n) \; | \; b$

gilt. Die Lösungen können dann durch Kombination der Lösungen der homogenen Gleichung mit einer Partikulärlösung, welche mit dem erweiterten Euklidischen Algorithmus gefunden werden kann, angegeben werden.

Beispiel

Es sind die ganzzahligen Lösungen x = (x₁,x₂) der linearen Diophantischen Gleichung

$2x_1 + 3x_2 \; = \; 26$

gesucht. Da die Koeffizienten a₁ = 2 und a₂ = 3 teilerfremd sind ist die Gleichung lösbar. Die Gesamtheit der Lösungen ist hier gegeben durch

$x \; = \; (3t+13, -2t)$    mit    $t \in \mathbb{Z}.$

Lineare Vektorgleichungen

→ Hauptartikel: Lineares Gleichungssystem

Wählt man die Vektorräume $V = \mathbb{R}^n$ und $W = \mathbb{R}^m$ sowie

$T(x) \; = \; A\;\cdot\;x \; = \; \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{pmatrix} \; = \; \begin{pmatrix} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n \\ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n \\ \vdots \\ a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n \\ \end{pmatrix}$

wobei $A \in \mathbb{R}^{m, n}$ eine reelle $m \times n$-Matrix ist, erhält man die lineare Vektorgleichung

$A \cdot x \; = \; b$

mit rechter Seite $b \in \mathbb{R}^m$ und unbekanntem Vektor $x \in \mathbb{R}^n$, welche gerade ein lineares Gleichungssystem darstellt. Eine lineares Gleichungssystem entsteht also durch Zusammenfassen von mehreren skalaren linearen Gleichungen mit ein oder mehreren Unbekannten zu einer Einheit. Die Lösungsmenge eines linearen Gleichungssystems ist dann die Schnittmenge der Lösungen der einzelnen Gleichungen. Ein lineares Gleichungssystem ist genau dann lösbar, wenn der Rang der Koeffizientenmatrix A gleich dem Rang der erweiterten Koeffizientenmatrix $(A\;b)$ ist. Lineare Gleichungssysteme können beispielsweise mit Hilfe des Gaußschen Eliminationsverfahrens gelöst werden.

Beispiel

Die allgemeine Lösung des linearen Gleichungssystems mit zwei Gleichungen und drei Unbekannten

$\begin{pmatrix} 1 & 2 & 3\\ -1 & 2 & 5\\ \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \end{pmatrix} \; = \; \begin{pmatrix} 10 \\ 6 \\ \end{pmatrix}$

ist gegeben durch

$x \; = \; \begin{pmatrix} t+4 \\ -2t \\ t+2 \\ \end{pmatrix}$    mit    $t \in \mathbb{R}.$

Lineare Differenzengleichungen

→ Hauptartikel: Lineare Differenzengleichung

Wählt man die Vektorräume V = W = ω als Folgenräume und

$T((x_n)_n) \; = \; \sum_{i=0}^k a_i(n) x_{n-i}$

erhält man die lineare Differenzengleichung k-ter Ordnung

$a_0(n) x_n + a_1(n) x_{n-1} +\;\cdots \; + a_k(n) x_{n-k} \; = \; b(n)$    für    $n \in \mathbb{N}, n \geq k$,

wobei die Unbekannte $(x_n)_n \in \omega$ eine Folge ist und $a_0(n), \ldots , a_k(n)$ sowie b(n) Koeffizienten sind, die zwar von n abhängen dürfen, aber unabhängig von den Gliedern der gesuchten Folge sein müssen. Die Lösung einer Differenzengleichung hängt von den Startwerten $x_0, \ldots , x_{k-1}$ ab und ist dann eindeutig definiert. Lineare Differenzengleichungen können durch Kombination der Lösung der homogenen Gleichung, die mit Hilfe der charakteristischen Gleichung gefunden werden kann, mit einer Partikulärlösung explizit gelöst werden.

Beispiel

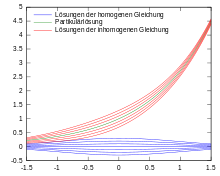
Die lineare Differenzengleichung erster Ordnung mit konstanten Koeffizienten

$x_n - 2 x_{n-1} \; = \; 3$

besitzt für den Startwert x₀ = c die Lösung

$x_n \; = \; (c+3)2^n-3.$

Lineare gewöhnliche Differentialgleichungen

Lösungen der linearen gewöhnlichen Differentialgleichungen $\scriptstyle f'(x) + x f(x) = 0$ (blau) und $\scriptstyle f'(x) + x f(x) = (1+x)e^x$ (rot,grün)

→ Hauptartikel: Lineare gewöhnliche Differentialgleichung

Wählt man die Vektorräume V und W als Funktionenräume mit stetig differenzierbaren Funktionen $f \in C^n$ und $g \in C^0$, erhält man durch Wahl von T als linearen gewöhnlichen Differentialoperator n-ter Ordnung

$T(f) = \left( \sum_{i=0}^n a_i(x) \frac{d^i}{dx^i} \right) f$

die lineare gewöhnliche Differentialgleichung

$a_n(x) f^{(n)}(x) + \cdots + a_1(x) f'(x) + a_0(x) f(x) \; = \; g(x)$

wobei die Koeffizientenfunktionen $a_0, \ldots , a_n$ und die rechte Seite g zwar von x, aber nicht von der gesuchten Funktion f und deren Ableitungen $f', \ldots , f^{(n)}$ abhängen dürfen. Ist f eine vektorwertige Funktion spricht man von einem linearen Differentialgleichungssystem. Die Existenz und Eindeutigkeit der Lösung gewöhnlicher Differentialgleichungen erster Ordnung gibt der Satz von Picard-Lindelöf. Die allgemeine Lösung der homogenen Gleichung kann über das zugehörige Fundamentalsystem angegeben werden, eine Partikulärlösung kann beispielsweise mittels der Variation der Konstanten gefunden werden.

Beispiel

Die Lösungen der gewöhnlichen Differentialgleichung erster Ordnung

$f'(x) + x f(x) \; = \; (1+x)e^x$

sind Funktionen der Form

$f(x) \; = \; k e^{-x^2/2} + e^x$     mit     $k \in \mathbb{R}$

Durch Wahl einer Anfangsbedingung, beispielsweise f(0) = k + 1, ist die Lösung dann eindeutig bestimmt.

Lineare partielle Differentialgleichungen

Lösung der Wärmeleitungsgleichung $\scriptstyle f_t - f_{xx} = \pi^2 \sin(\pi x)$

Sind die Vektorräume V und W ebenfalls Funktionenräume, wobei $f \in C^n$ und $g \in C^0$ stetig differenzierbare Funktionen mehrerer Veränderlicher sind, erhält man durch Wahl von T als linearen partiellen Differentialoperator n-ter Ordnung

$T(f) = \left(\sum_{\alpha_1=0}^n \cdots \sum_{\alpha_m=0}^n a_{\alpha}(x) \frac{\partial^{|\alpha|}}{\partial x_1^{\alpha_1} \cdots \partial x_m^{\alpha_m}}\right) f$

die lineare partielle Differentialgleichung

$\sum_{\alpha_1=0}^n \cdots \sum_{\alpha_m=0}^n a_{\alpha}(x) \frac{\partial^{|\alpha|}f(x)}{\partial x_1^{\alpha_1} \cdots \partial x_m^{\alpha_m}} \; = \; g(x)$

wobei $x = (x_1, \ldots , x_m)$, $\alpha = (\alpha_1, \ldots , \alpha_m)$ und $|\alpha| = \alpha_1 + \ldots + \alpha_m$ sind. Wiederum dürfen die Koeffizientenfunktionen a_α und die rechte Seite g zwar von den Koordinaten x₁ bis x_m, aber nicht von der gesuchten Funktion f und deren partiellen Ableitungen abhängen. Damit die Lösung einer partiellen Differentialgleichung eindeutig bestimmt ist, müssen Anfangs- und/oder Randbedingungen vorgegeben werden. Zur Lösung linearer partieller Differentialgleichungen gibt es verschiedene Ansätze, beispielsweise Fundamentallösungen, die Methode der Charakteristiken oder der Separationsansatz.

Beispiel

Die Lösung der eindimensionalen Wärmeleitungsgleichung für die unbekannte Funktion f(x,t)

$\frac{\partial f}{\partial t} - \frac{\partial^2 f}{\partial x^2} \; = \; \pi^2 \sin(\pi x)$

als Anfangs-Randwertproblem im Streifen $[0,1] \times [0,\infty)$ mit den Dirichlet-Randbedingungen $f(0,t) \; = \; f(1,t) \; = \; 0$ und der Anfangsbedingung $f(x,0) \; = \; 2 \sin(\pi x)$ erhält man mittels des Separationsansatzes als

$f(x,t) \; = \; \sin(\pi x)(e^{-\pi^2t}+1).$

Lineare Integralgleichungen

Sind die Vektorräume V und W Funktionenräume ausreichender Integrierbarkeit, erhält man durch Wahl von T als linearen Integraloperator

$T(f) = \lambda f(x) + \int_a^x K(x,y) f(y)~dy$

mit Integralkern K(x,y) und konstantem Vorfaktor λ die lineare Integralgleichung

$\lambda f(x) + \int_a^x K(x,y) f(y)~dy \; = \; g(x)$

welche im allgemeinen Fall eine Volterra-Integralgleichung 2. Art darstellt. Sind beide Integrationsgrenzen fest, so handelt es sich um eine Fredholm-Integralgleichung. Ist λ = 0 spricht man von einer Integralgleichung 1. Art.

Beispiel

Die Volterra-Integralgleichung 1. Art

$\int_0^x (x-y) f(y)~dy \; = \; x^3$

wird durch

$f(x) \; = \; 6x$

gelöst.

Weitere lineare Operatorgleichungen

Beispiele für weitere lineare Operatorgleichungen mit Funktionen als Unbekannten sind:

• Lineare differential-algebraische Gleichungen
• Lineare Integro-Differentialgleichungen
• Lineare stochastische Differentialgleichungen

Siehe auch

• Quadratische Gleichung
• Kubische Gleichung
• Quartische Gleichung

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2008, ISBN 3-540-34186-2.
• Bernd Aulbach: Gewöhnliche Differenzialgleichungen. 2. Auflage. Spektrum Akademischer Verlag, 2004, ISBN 3-827-41492-X.
• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 7. Auflage. Vieweg, 2009, ISBN 3-528-66508-4.
• Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer-Verlag, 2010, ISBN 3-540-76490-9.
• Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 17. Auflage. Vieweg Verlag, 2009, ISBN 3-834-80996-9.
• Jürgen Jost: Partielle Differentialgleichungen: Elliptische (und parabolische) Gleichungen. 1. Auflage. Springer-Verlag, 2009, ISBN 3-540-64222-6.