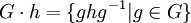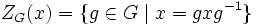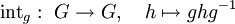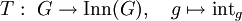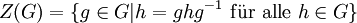Konjugationsklasse

Die Konjugationsoperation ist eine Gruppenoperation, die eine Gruppe in Konjugationsklassen zerlegt. Die Elemente einer Konjugationsklasse haben viele Gemeinsamkeiten, sodass eine nähere Betrachtung dieser Klassen wichtige Einblicke in die Struktur nicht-abelscher Gruppen ermöglicht. Bei abelschen Gruppen sind Konjugationsklassen nebensächlich, da jedes Gruppenelement eine eigene Konjugationsklasse bildet.

Konjugationsoperation

Die Konjugationsoperation ist eine Operation einer Gruppe auf sich selbst, die folgendermaßen definiert ist:

$\alpha: \ G \times G \rightarrow G, \quad (g,h) \mapsto ghg^{-1}$

Zwei Elemente h₁ und h₂ einer Gruppe heißen zueinander konjugiert, wenn es ein Element 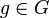$g \in G$ gibt, sodass h₁ = gh₂g ^{− 1} ist. Die Konjugiertheit ist eine Äquivalenzrelation. Sie besitzt also folgende Eigenschaften:

• Jedes Element h ist konjungiert zu sich selbst (Reflexivität).
• Ist h₁ konjungiert zu h₂, so ist auch h₂ konjungiert zu h₁ (Symmetrie).
• Ist h₁ konjungiert zu h₂ und h₂ konjungiert zu h₃, dann ist auch h₁ konjungiert zu h₃ (Transitivität).

Alle Elemente, die zueinander konjungiert sind, bilden jeweils eine Äquivalenzklasse, die sogenannte Konjugationsklasse von h:

$G \cdot h = \{ghg^{-1} | g \in G\}$

Dabei kann als h ein beliebiges Element der Konjugationsklasse gewählt werden. Die Konjugationsklassen sind die Bahnen der Konjugationsoperation.

Die Fixgruppe

$Z_G(x) = \{ g\in G \mid x=gxg^{-1} \}$

eines Elementes x ist der Zentralisator von x.

Eine Untergruppe N einer Gruppe G ist invariant unter Konjugation, wenn für alle Elemente h aus N und alle Elemente g aus G das Produkt ghg ^{− 1} wieder in N liegt:

gNg ^{− 1} = N

Eine unter Konjugation invariante Untergruppe einer Gruppe wird als Normalteiler der Gruppe bezeichnet. Normalteiler erlauben die Bildung von Faktorgruppen der Gruppe.

Konjugation

Die Konjugation mit g ist die Abbildung

$\operatorname{int}_g: \ G \rightarrow G, \quad h \mapsto ghg^{-1}$

Sie entsteht aus der Konjugationsoperation indem g festgehalten wird. Die Konjugation ist ein innerer Automorphismus von G. Daher kommt auch die Bezeichnung 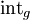$\operatorname{int}_g$, bei der das „int“ für „interior“ steht. ^[1]

Die Abbildung

$T: \ G \rightarrow \operatorname{Inn}(G), \quad g \mapsto \operatorname{int}_g$

bildet G in die Gruppe der inneren Automorphismen 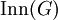$\operatorname{Inn}(G)$, einen Normalteiler der Automorphismengruppe, ab.

Der Kern von T ist das Zentrum Z(G) von G:

$Z(G) = \{ g \in G | h = ghg^{-1} \mathrm{\ f\ddot{u}r\ alle\ } h \in G\}$

Die Abbildung T vermittelt also einen Isomorphismus von G / Z(G) nach $\operatorname{Inn}(G)$.

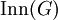Einzelnachweise

1. ↑ Siegfried Bosch: Algebra. Springer, 2004, ISBN 3-540-40388-4, S. 239