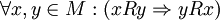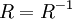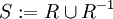Symmetrie (Mengenlehre)

Drei symmetrische Relationen, als gerichtete Graphen dargestellt

Die Symmetrie einer zweistelligen Relation R auf einer Menge ist gegeben, wenn aus x R y stets y R x folgt. Man nennt R dann symmetrisch.

Die Symmetrie ist eine der Voraussetzungen für eine Äquivalenzrelation.

Formale Definition

Ist M eine Menge und 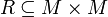$R \subseteq M \times M$ eine zweistellige Relation auf M, dann heißt R symmetrisch, wenn (unter Verwendung der Infixnotation) gilt:

$\forall x, y \in M: (x R y \Rightarrow y R x)$

Beispiele

Gleichheit der reellen Zahlen

Die gewöhnliche Gleichheit $=\$ auf den reellen Zahlen ist symmetrisch, denn aus x = y folgt y = x. Sie ist darüber hinaus eine Äquivalenzrelation.

Die Ungleichheitsrelation 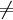$\neq\$ auf den reellen Zahlen ist zwar keine Äquivalenzrelation, aber ebenfalls symmetrisch, denn aus 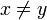$x \neq y$ folgt $y \neq x$.

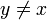Ähnlichkeit von Dreiecken

Ist das Dreieck ABC zum Dreieck DEF ähnlich, so ist das Dreieck DEF zum Dreieck ABC ähnlich. Die Relation der Ähnlichkeit von Dreiecken ist also symmetrisch. Sie ist darüber hinaus eine Äquivalenzrelation.

Kongruenz modulo n

Eine natürliche Zahl a heißt zu der natürlichen Zahl b kongruent modulo n, wenn a und b bei der Division durch n denselben Rest haben. Beispielsweise ist die Zahl 11 zur Zahl 18 kongruent modulo 7, da sich bei der Division dieser beiden Zahlen durch 7 jeweils der Rest 4 ergibt. Diese Relation ist symmetrisch. Sie ist darüber hinaus eine Äquivalenzrelation.

Ordnung der reellen Zahlen

Die Kleiner-Relation 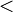$&amp;amp;lt;\$ auf den reellen Zahlen ist nicht symmetrisch, denn x < y und y < x können nicht gleichzeitig gelten.

Darstellung als gerichteter Graph

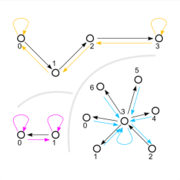
Jede beliebige Relation R auf einer Menge M kann als gerichteter Graph aufgefasst werden (Beispiel siehe oben). Die Knoten des Graphen sind dabei die Elemente von M. Vom Knoten a zum Knoten b wird genau dann eine gerichtete Kante (ein Pfeil 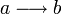$a \longrightarrow b$) gezogen, wenn a R b gilt.

Die Symmetrie von R lässt sich im Graphen nun so charakterisieren: Wann immer es einen Pfeil 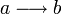$a \longrightarrow b$ zwischen verschiedenen Knoten a und b des Graphen gibt, dann gibt es gleichzeitig einen Pfeil $b \longrightarrow a$. (Einen Graphen mit dieser Eigenschaft nennt man auch symmetrischer Graph.)

Pfeile $a \longrightarrow a$ spielen bei diesem Kriterium keine Rolle.

Eigenschaften

• Mit Hilfe der konversen Relation R ^{− 1} lässt sich die Symmetrie einer Relation R charakterisieren durch

  $R = R^{-1}\$

• Ist die Relation R symmetrisch, dann gilt dies auch für die komplementäre Relation R^c. Diese ist definiert durch

  $x R^{\rm c} y :\Longleftrightarrow \neg x R y$.

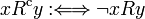• Sind die Relationen R und S symmetrisch, dann gilt dies auch für ihre Schnittmenge 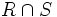$R \cap S$ und ihre Vereinigungsmenge 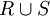$R \cup S$. Diese Aussage lässt sich von zwei Relationen auf den Durchschnitt 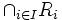$\cap_{i\in I} R_i$ und die Vereinigung 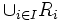$\cup_{i\in I} R_i$ einer beliebigen (nichtleeren) Familie von symmetrischen Relationen verallgemeinern.
• Die kleinste symmetrische Relation S, die eine gegebene Relation R umfasst, wird der symmetrische Abschluss von R genannt. Dieser lässt sich leicht angeben als

  $S := R \cup R^{-1}\$

• Zu einer beliebigen zweistelligen Relation R auf einer Menge lassen sich die Potenzen Rⁿ bezüglich der Verkettung von Relationen bilden. Ist nun R symmetrisch, dann gilt dies auch für alle Potenzen Rⁿ.
• Eine Relation (auf einer endlichen Menge) ist genau dann symmetrisch, wenn die ihrem Graphen zugeordnete Adjazenzmatrix symmetrisch (zur Hauptdiagonale) ist.

Siehe auch

• Antisymmetrie
• Asymmetrie