Kontextfreie Grammatiken

Die kontextfreien Grammatiken sind eine Klasse formaler Grammatiken und sind identisch mit den Typ-2-Grammatiken der Chomsky-Hierarchie.

Definition

Eine kontextfreie Grammatik G ist definiert durch das 4-Tupel (N,T,P,S), wobei N die Menge der Nichtterminal-Symbole, T die Menge der Terminal-Symbole, P die Menge der Grammatik-Produktionen und 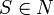$S\in N$ das Startsymbol der Grammatik bezeichnet:

1. G = (N,T,P,S)
2. $S\in N$
3. $N \cap T = \emptyset$
4. $P = \{ (X_r \rightarrow y_1\ldots y_{l_r}) | X_r\in N, y_i\in (N\cup T),1\leq i\leq l_r\}$

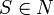
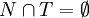
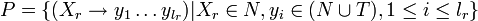
Eine kontextfreie Grammatik G = (N,T,P,S) ist eine Grammatik, deren Produktionsregeln soweit eingeschränkt sind, dass immer genau ein Nichtterminal auf eine beliebig lange Folge von Nichtterminalen und Terminale abgeleitet wird. In jeder Produktion steht das Nichtterminal auf der linken Seite frei, es kann nicht von einem Kontext von anderen Symbolen umgeben sein. Mathematisch wird dies durch 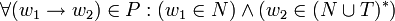$\forall (w_1 \rightarrow w_2) \in P : ( w_1 \in N) \and \left(w_2 \in (N \cup T)^*\right)$ beschrieben.

Man schreibt $G \in \mbox{Typ}_2$.

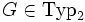Eine Erweiterung der kontextfreien Grammatiken bilden die stochastischen kontextfreien Grammatiken. Hier wird jeder Produktionsregel eine Auftrittswahrscheinlichkeit zugeordnet:

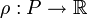$\rho: P\rightarrow\mathbb{R}$ mit $\sum_{p \in P} \rho(p) = 1$

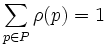
Normalformen

Für kontextfreie Grammatiken sind verschiedene Normalformen definiert. Unter der Chomsky-Normalform (CNF) sind die rechten Seiten der Nichtterminal-Produktionen eingeschränkt, d.h. auf der rechten Seite darf entweder ein einziges Terminal-Symbol oder genau zwei Nichtterminal-Symbole stehen. Wenn das Startsymbol auf der linken Seite steht, darf die rechte Seite der Produktion das leere Wort erzeugen. Durch einen Algorithmus kann jede kontextfreie Grammatik in die CNF überführt werden.

Eine kontextfreie Grammatik ist in der Greibach-Normalform (GNF), wenn sie nicht das leere Wort erzeugt und die rechten Seiten der Produktionen mit maximal einem Terminal-Symbol beginnen und sonst nur Nichtterminal-Symbole enthalten. Jede kontextfreie Grammatik, die nicht das leere Wort erzeugt kann mit einem Algorithmus in die GNF überführt werden.

Von G erzeugte Sprache

Die kontextfreien Grammatiken erzeugen genau die kontextfreien Sprachen, d. h. jede Typ-2-Grammatik erzeugt eine kontextfreie Sprache und zu jeder kontextfreien Sprache existiert eine Typ-2-Grammatik, die diese erzeugt.

Die kontextfreie Sprache L, die durch die kontextfreie Grammatik G generiert wird, ist formal definiert als L(G) mit:

$L(G) = \{ w | w\in T^*, S \rightarrow_G^* w \}$

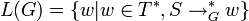
Das Symbol 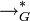$\rightarrow_G^*$ steht für eine Reihe von Produktionsanwendungen unter der Grammatik G, an deren Ende das Wort w der Sprache L(G) abgeleitet werden kann. Es gilt also $L(G)\subset T^*$.

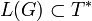Die kontextfreien Sprachen sind genau die Sprachen, die von einem nichtdeterministischen Kellerautomaten akzeptiert werden. Existiert auch ein deterministischer Kellerautomat, nennt man die Grammatik auch deterministisch kontextfrei. Diese Teilmenge der kontextfreien Sprachen bildet die theoretische Basis für die Syntax der meisten Programmiersprachen.

Kontextfreie Sprachen können das leere Wort enthalten, z.B. durch eine Produktionsregel 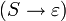$(S \rightarrow \varepsilon)$. Einige Sätze über kontextfreie Grammatiken fordern allerdings zusätzlich, dass das leere Wort von ihr nicht erzeugt werden darf. So gibt es z.B. nur zu den kontextfreien Grammatiken eine äquivalente Grammatik in Greibach-Normalform, wenn das leere Wort durch sie nicht erzeugt werden kann, da in jedem Ableitungsschritt genau ein Terminal erzeugt wird.

Eigenschaften

Das Wortproblem für kontextfreie Sprachen, also das Problem, ob ein Wort w von einer kontextfreien Grammatik erzeugt werden kann, ist entscheidbar^[1]. Auf dem Weg der Lösung des Wortproblems, kann zusätzlich ein Ableitungsbaum erzeugt werden. Dieser Ableitungsbaum wird auch Parse-Tree genannt und ein Programm welches einen Parse-Tree erzeugt ist ein Parser. Für jede kontextfreie Grammatik kann automatisch ein Parser generiert werden (siehe auch CYK-Algorithmus). Die Worst-Case-Laufzeitkomplexität von einem Parser für eine beliebige kontextfreie Grammatik liegt in O(n³). Für Teilklassen von kontextfreien Grammatiken können Parser erzeugt werden, deren Laufzeit in O(n) liegt. Ein typischer Anwendungsfall von einem effizienten kontextfreien Parser mit linearer Laufzeit ist das parsen von einer Programmiersprachen-Quelltext-Datei in einem Compiler.

Wenn ein Wort w der Sprache L (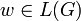$w\in L(G)$) durch die Grammatik G auf mehrere verschiedene Arten erzeugt werden kann, dann ist diese Grammatik mehrdeutig. Ein Parser kann bei einer mehrdeutigen Grammatik nicht nur einen sondern mehrere Ableitungsbäume erzeugen. Mehrdeutigkeit ist nicht problematisch, wenn nur das Wortproblem gelöst wird. Wird aber den unterschiedlichen Ableitungsbäumen eine unterschiedliche Bedeutung zugeordnet, dann kann eine Eingabe unter einer mehrdeutigen Grammatik mehrere unterschiedliche Bedeutungen haben. Ein Beispiel für die Notwendigkeit einer eindeutigen kontextfreieen Grammatik ist ein Compiler, der für jede gültige Eingabe deterministisch und eindeutig ausführbaren Zielcode erzeugen muss.

Das Problem, ob eine (beliebige) kontextfreie Grammatik mehrdeutig oder nicht-mehrdeutig ist, ist nicht entscheidbar^[2]. Es existieren aber Testverfahren, die für bestimmte Teilklassen von kontextfreien Grammatik Mehrdeutigkeit bzw. Nicht-Mehrdeutigkeit feststellen können^[3]. Je nach Testverfahren, terminiert der Mehrdeutigkeit-Test nicht oder der Test liefert zurück, dass die Mehrdeutigkeit nicht festgestellt werden kann, falls die kontextfreie Eingabe-Grammatik nicht Element einer bestimmten Teilklasse von kontextfreien Grammatiken ist.

Beispiele

Sei G = (N,T,P,S) eine kontextfreie Grammatik mit

T = {x,y,z}

N = {S,A,B}

P enthält 4 Produktionen bzw. Produktionsregeln:

$\begin{align} S & \rightarrow & A \\ A & \rightarrow & x A y \\ A & \rightarrow & x B y \\ B & \rightarrow & z \end{align}$

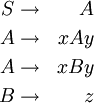
w₁ = xxzyy kann durch die Grammatik G mit folgender Ableitung erzeugt werden:

t(w₁) = S(A(x,A(x,B(z),y),y))

t(w₁) ist der Ableitungsbaum in Term-Schreibweise. Die Wurzel und die inneren Knoten sind mit Nichtterminal-Symbolen und die Blätter mit Terminal-Symbolen beschriftet.

Also ist $w_1\in L(G)$.

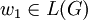Das Beispiel Wort w₂ mit w₂ = z ist nicht Teil der Sprache L(G), da das Nichtterminal B nicht das Startsymbol ist und über das Startsymbol jedes Wort der Sprache von den Terminal-Symbolen x und y eingeschlossen sein muss. In Formelschreibweise:

$w_2\notin L(G)$

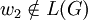
Grammatik G ist nicht mehrdeutig.

Mehrdeutiges Beispiel

Ein Beispiel für eine mehrdeutige Grammatik ist G₂ = (N₂,T₂,P₂,S₂).

T₂ = {x,y}

N₂ = {S₂,A}

P₂ enthält folgende Produktionen:

$\begin{align} S_2 & \rightarrow & A \\ A & \rightarrow & AA \\ A & \rightarrow & x A y \\ A & \rightarrow & \varepsilon \end{align}$

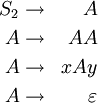
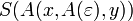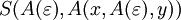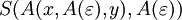Für w₃ = xy existieren die Ableitungen $S(A(x,A(\varepsilon),y))$, $S(A(\varepsilon),A(x,A(\varepsilon),y))$ und $S(A(x,A(\varepsilon),y),A(\varepsilon))$. Also ist G₂ mehrdeutig.

Siehe auch

• Backus-Naur-Form
• Tree Adjoining Grammar

Einzelnachweise

1. ↑ Schöning, 2001, S.21
2. ↑ Alfred V. Aho and Jeffrey D. Ullman: The Theory of Parsing, Translation, and Compiling. Volume 1: Parsing. Prentice-Hall, 1972, ISBN 0-13-914556-7, S. 202. 
3. ↑ H. J. S. Basten: Ambiguity Detection Methods for Context-Free Grammars. (http://homepages.cwi.nl/~paulk/thesesMasterSoftwareEngineering/2007/BasBasten.pdf ; Master Thesis). 

Literatur

• Uwe Schöning: Theoretische Informatik - kurzgefasst. 4. Auflage. Spektrum Akademischer Verlag, 2001, ISBN 3-8274-1099-1, S. 13,51.