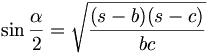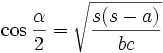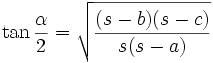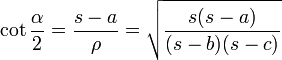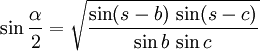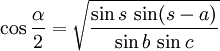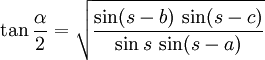Kotangenssatz

Die Halbwinkelsätze sind Formeln der Trigonometrie, die für spezielle, logarithmisch brauchbare Anwendungsfälle zur Ermittlung der Bestimmungsgrößen (Seiten a, b, c; Winkel α, β, γ) von allgemeinen Dreiecken entwickelt wurden. Entsprechende Sätze gelten für allgemeine Dreiecke auf einer Kugeloberfläche (sphärische Geometrie).

Halbwinkelsätze in der Ebene

Datei:Unregelmaessiges Dreieck.png

• $\sin{\frac{\alpha}{2}} = \sqrt{\frac{(s-b)(s-c)}{bc}}$
• $\cos{\frac{\alpha}{2}} = \sqrt{\frac{s(s-a)}{bc}}$
• $\tan{\frac{\alpha}{2}} = \sqrt{\frac{(s-b)(s-c)}{s(s-a)}}$

wobei $s = \frac{a + b + c}{2}$

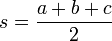
Die zur dritten Formel äquivalente Aussage

• $\cot{\frac{\alpha}{2}} = \frac{s-a}{\rho} = \sqrt{\frac{s(s-a)}{(s-b)(s-c)}}$

ist auch als Kotangenssatz bekannt. ρ bezeichnet hier den Inkreisradius.

Entsprechende Formeln gelten für die anderen Winkel.

Halbwinkelsätze auf der Kugeloberfläche

• $\sin{\frac{\alpha}{2}} = \sqrt{\frac{\sin(s-b) \, \sin(s-c)}{\sin b \, \sin c}}$
• $\cos{\frac{\alpha}{2}} = \sqrt{\frac{\sin s \, \sin(s-a)}{\sin b \, \sin c}}$
• $\tan{\frac{\alpha}{2}} = \sqrt{\frac{\sin(s-b) \, \sin(s-c)}{\sin s \, \sin (s-a)}}$

wobei $s = \frac{a + b + c}{2}$