Kritischer Winkel

Der kritischer (Einfalls-)Winkel ist ein Begriff aus der Physik und wird gebraucht im Zusammenhang mit der Brechung von Wellen. Gebräuchlich ist der Begriff insbesondere in der Optik und in der Refraktionsseismik.

Beschreibung

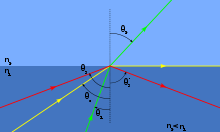Totalreflexion (rot und gelb): Interne Reflexion beim Auftreffen von Licht vom optisch dichteren auf ein optisch dünneres Medium (Goos-Hänchen-Effekt wird vernachlässigt)

Die Brechung von Wellen, das heißt, die Änderung des Verlaufs beim Übergang einer Welle von einem Medium in ein angrenzendes Medium, basiert auf einer Änderung ihrer Ausbreitungsgeschwindigkeit. Diese wird durch das durchquerte Medium festgelegt (vgl. Brechzahl, snelliussches Brechungsgesetz)

Betrachtet man beispielsweise eine elektromagnetische Welle (wie sichtbares Licht), die sich in einem Medium 1 ausbreitet und unter einem bekannten Einfallswinkel α auf eine Grenzfläche zu einem Medium 2 auftrifft. So wird diese gemäß der Fresnel-Gleichungen zum Teil reflektiert bzw. transmittiert, das heißt, das Licht geht in das Medium 2 über. Bei diesem Übergang erfährt der Lichtstrahl (kann als Interferenz der Lichtwellen betrachtet werden) gemäß dem snelliusschen Brechungsgesetz eine Richtungsänderung, er wird „gebrochen“ (grüner Strahlenverlauf im Bild).

n₁sin(θ₁) = n₂sin(θ₂)

Das bedeutet für einen Übergang von einem Medium 1 in ein optisch dichteres Medium 2 (c₁ > c₂, n₁ < n₂), dass der Strahl zum Lot hingebrochen wird, beispielsweise beim Übergang Luft in Wasser. c₁,c₂ stehen hierbei für die Ausbreitungsgeschwindigkeiten und n₁,n₂ für die Brechzahlen der beiden Medien.

Im umgekehrten Fall (der Lichtstrahl kommt aus dem Wasser) wird er hingegen vom Lot weg gebrochen. Vergrößert man nun den Einfallswinkel θ₁, so verläuft der gebrochene Strahl ab einem bestimmten Wert parallel zur Grenzfläche (gelber Strahlenweg). Dieser Winkel wird Grenzwinkel der Totalreflexion oder auch kritischer Winkel θ_c genannt. Der Winkel der Totalreflexion lässt sich mithilfe des snelliusschen Brechungsgesetzes berechnen:

$\theta_{\mathrm c} = \arcsin\!\left(\frac{n_2}{n_1}\right).$

Die Abhängigkeit des Strahlwegs von der Ausbreitungsgeschwindigkeit gilt gleichermaßen auch für seismische Wellen. In diesem Fall der mechanischen Wellenausbreitung stellt der „Wellenstrahl“ die senkrechte Trajektorie der Wellenfront dar. Verändert sich nun die Ausbreitungsgeschwindigkeit, wird dadurch die Lage der Wellenfront und somit auch der Strahlweg verändert. Da eine Brechzahl für mechanische Wellen nicht existiert, ist das snelliussche Brechungsgesetz in der Seismik über die Ausbreitungsgeschwindigkeiten (v₁,v₂) der durchlaufenen Medien definiert:

$\frac{\sin(\theta_1)}{v_1} = \frac{\sin(\theta_2)}{v_2}$

Der kritische Winkel ist demnach zu berechnen aus:

$\theta_{\mathrm c} = \arcsin\!\left(\frac{v_1}{v_2}\right).$

Im Gegensatz zu elektromagnetischen Wellen, deren Ausbreitungsgeschwindigkeit – wie am Beispiel eines Lichtstrahls erläutert – im optisch dichteren Medium abnimmt, nimmt diese bei seismischen Wellen zu, wenn die Wellenfront in ein kompakteres Medium eintritt. Eine kritische Refraktion tritt bei seismischen Wellen daher beim Übergang von einem lockereren in ein festeres Gestein auf.

Der Effekt der seismischen kritischen Refraktion wird in der Methode der Refraktionsseismik gezielt zur Untersuchung von Schichtstrukturen des Erdinneren ausgenutzt: Im Regelfall wachsen die seismischen Geschwindigkeiten mit zunehmender Tiefe an, so dass beim Auftreffen einer seismischen Wellen auf eine Schichtgrenze unter dem kritischen Winkel eine refraktierte Welle entsteht. Diese sogenannte Kopfwelle breitet sich entlang der Schichtgrenze mit der Geschwindigkeit der unteren Schicht aus. Dabei strahlt sie kontinuierlich seismische Wellenenergie ab, die wiederum unter dem kritischen Winkel zurück an die Oberfläche läuft, wo sie aufgezeichnet werden und zur Bestimmung der Ausbreitungsgeschwindigkeit benutzt werden kann.